水下爆炸作用下艦船總縱強度模型實驗方案研究
張海鵬,岳永威,蘇羅青,張阿漫,姚熊亮
(哈爾濱工程大學(xué) 船舶工程學(xué)院,哈爾濱 150001)
提高艦船的抗爆抗沖擊性能和生命力是保證艦船發(fā)揮其作戰(zhàn)能力[1]的一項重要前提,各國海軍十分重視該方面的研究。對艦船進行實船爆炸實驗是評估艦船總縱強度最準(zhǔn)確有效的方式,但需要耗費大量的資金,且實施較為困難。因此,許多發(fā)展中國家在評估艦船水下爆炸作用下的總縱強度[2-3]方面,基本上采用艦船縮比模型開展水下爆炸實驗來評估,此時會產(chǎn)生這樣的矛盾:若縮尺比較大,則實驗費用居高不下,開展縮比模型實驗的意義大為降低;若縮尺比較小,縮比模型的尺寸會非常小,模型在制造工藝上存在較大困難,且換算到實船上結(jié)果的準(zhǔn)確性也得不到保證,我國雖然開展了一些縮比模型的水下爆炸實驗,但其縮尺比均較小,模型與實船既未能達到完全幾何相似,也不存在畸變相似關(guān)系,因此其實驗結(jié)果難以評估與考核實船的抗爆抗沖能力。
在評估艦船總縱強度水下爆炸實驗中,若采用合適的縮尺比,再以此艦船縮比模型為基準(zhǔn)模型,根據(jù)彈性結(jié)構(gòu)畸變準(zhǔn)則,選擇合適的畸變參數(shù)對基準(zhǔn)模型中幾何尺寸較小的板梁進行畸變,使用畸變模型進行實驗。這樣,不僅能解決模型在制造工藝中的困難,還可以在降低實驗成本的前提下實現(xiàn)準(zhǔn)確預(yù)測艦船原型總縱強度的目的。本文的加載方式考慮了水下爆炸沖擊波和氣泡載荷的一次相似律,并利用彈性結(jié)構(gòu)畸變準(zhǔn)則對基準(zhǔn)模型進行畸變,通過數(shù)值計算手段得到滿足工程精度、制造工藝、經(jīng)濟性等要求的艦船總縱強度模型實驗方案。
1 縮比模型水下爆炸相似規(guī)律
多年來,國內(nèi)外許多學(xué)者一直致力于水下爆炸“相似律”的研究和探索,尋求通過縮比模型實驗預(yù)測原型結(jié)構(gòu)動響應(yīng)特性的方法,現(xiàn)今也取得了許多具有學(xué)術(shù)價值[4]的成果。水下爆炸是一個很復(fù)雜的物理過程,分為沖擊波和氣泡脈動兩個階段,流體的特性也會在不同的階段發(fā)生變化,如果簡單的將模型加載方式用同一個沖擊波、氣泡脈動相似準(zhǔn)則處理,得到的模型實驗數(shù)據(jù)結(jié)論將與原型發(fā)生偏差,甚至背離。因此需要對水下爆炸產(chǎn)生的沖擊波和氣泡的相似律分別討論。另外在工程實際中,某些時候縮比模型的相似條件不能滿足,如模型中的板或梁的幾何尺寸按縮尺比進行縮尺,縮比后的模型在制作中會產(chǎn)生諸多問題,如焊接難度大、所需規(guī)格市場上不存在,因此就必須利用彈性結(jié)構(gòu)的完全相似理論及畸變準(zhǔn)則對基準(zhǔn)模型的結(jié)構(gòu)進行改造得到畸變模型,最終實現(xiàn)對原型總縱強度的準(zhǔn)確預(yù)測。
1.1 沖擊波載荷相似律
自由場中水下爆炸沖擊波現(xiàn)象區(qū)別于一般水動力學(xué)現(xiàn)象,它的作用力是瞬態(tài)的并且具有很強的沖量,水動力學(xué)中一些相似常數(shù)(如Fr數(shù))可以不必討論。本文僅考慮自由場中的水下爆炸問題,要使自由場水下爆炸中沖擊波階段的過程相似,必須使各基本相似量間滿足一定的相似條件,即:


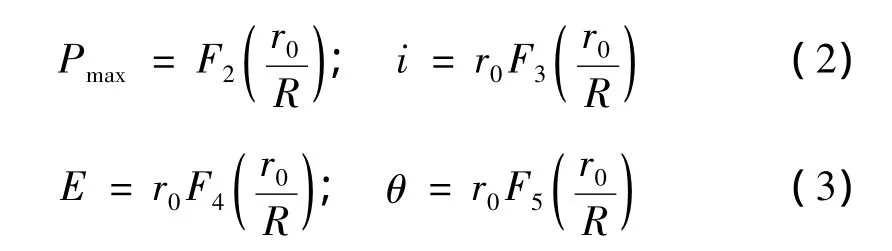
若用裝藥量W表示,即r0=,相似條件可利用經(jīng)驗公式[7]由已知的方程導(dǎo)出:
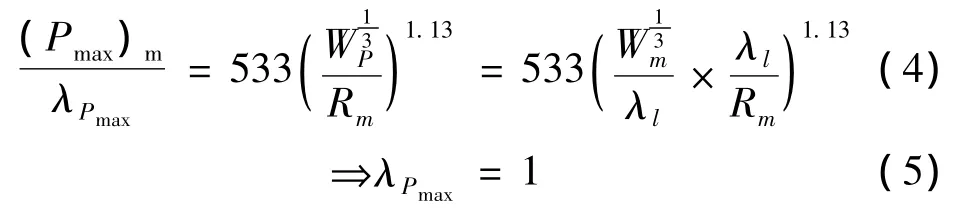

同理可求得:λE=λi=λθ=λl,即當(dāng)模型的幾何尺寸、加載形式與原型相似時,兩者的壓力峰值是相同的,而脈沖持續(xù)時間、沖量、比沖量、能量密度將按特征長度相似常數(shù)(λl)換算。
1.2 氣泡脈動載荷相似律
對于自由場中水下爆炸氣泡脈動問題,本文假定氣泡膨脹時周圍的水產(chǎn)生徑向運動,而沒有垂向位移,即不考慮與氣泡上浮時流體靜壓變化有關(guān)的流體靜浮力的影響[8]。在這個假定的條件下,要使自由場水下爆炸中氣泡脈動階段的過程相似,必須使各基本相似量間滿足一定的相似條件,即:

式中:Pd為爆深D(m)處靜水壓(Pa),等于D+D0(m)水柱壓強,D0為大氣壓的水柱壓強;為氣泡脈動壓力峰值;T為一次氣泡脈動周期;θ為衰減系數(shù);ρ0為裝藥密度;r0為裝藥半徑;Ep為單位質(zhì)量氣泡能;為氣泡最大半徑;ρw為水密度。選定Pd、ρw和r0為基本物理量,同樣由π定理得到各物理量函數(shù)關(guān)系式為:

以一次氣泡脈動周期項T項作為因變項,并用裝藥質(zhì)量及水柱表示,經(jīng)轉(zhuǎn)換得到Ep、和各物理量與周期的函數(shù)關(guān)系式分別用G3、G4和G5表示[6]:
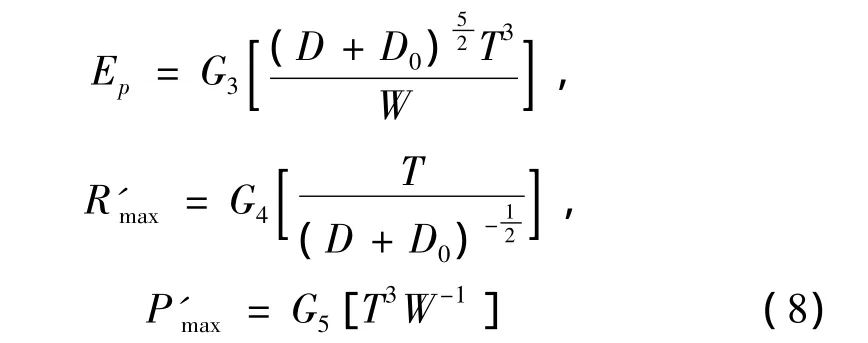
由經(jīng)驗公式[6]:

類比后求得關(guān)系式[6]:

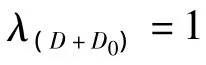
綜上所述,在不考慮重力效應(yīng)影響的情況下,自由場中氣泡脈動相似的的充分必要條件是:(D+D0)是個常量。要實現(xiàn)這一充要條件,必須使用將實驗水池做封閉增壓處理,在(D+D0)一定時,當(dāng)模型的幾何尺寸、加載形式與原型相似時,在一次氣泡脈動階段,氣泡最大半徑、脈動周期以及脈動頻率按特征長度相似常數(shù)(λl)換算,氣泡脈動峰值不變。事實上,以目前國內(nèi)的實驗條件,通過對水池進行封閉增壓來實現(xiàn)水下爆炸一次氣泡脈動的相似難以實現(xiàn),大部分模型試驗主要在露天水池中進行,此時(D+D0)就不可能是一個常量,對氣泡脈動的模擬就存在誤差,然而,要得到在不考慮對實驗水池進行封閉增壓處理時,大縮尺比船模水下爆炸實驗進行原型總縱強度預(yù)報的誤差范圍,還需要嚴(yán)格的理論推導(dǎo)及大量實驗,本文主要介紹水下爆炸實驗?zāi)P偷倪x取方法,這里不做詳細(xì)討論。
1.3 艦船模型畸變相似準(zhǔn)則
船體板格通常為矩形板,按邊界不同大致可分為剛性固定、彈性固定、彈性支持和簡支。下面以均布荷重P(t)作用下四邊剛性固定的矩形板為例,討論其板厚不能按特征長度相似常數(shù)λ縮小時的畸變修正方法。此時將均布荷重P(t)作用下四邊剛性固定的矩形板作為一個系統(tǒng),取表征系統(tǒng)這一現(xiàn)象的物理量:均布荷重P(t)、時間t、板厚d,t時刻的位移U(t)、t時刻的應(yīng)變ε(t)、t時刻的應(yīng)力σ(t)、材料泊松比μ、結(jié)構(gòu)固有頻率f、系統(tǒng)總能量Q、材料密度ρ、t時刻的結(jié)構(gòu)尺寸L(t)和彈性模量E,共12個物理量。當(dāng)縮比模型與原型使用同種材料時有:

當(dāng)板厚不能按特征長度相似常數(shù)λL(t)縮小時,定義完全幾何相似模型為基準(zhǔn)模型(上標(biāo)“m”代表基準(zhǔn)模型的∏項和物理量),以基準(zhǔn)模型為基礎(chǔ)僅對板厚進行畸變的模型定義為畸變模型(上標(biāo)“b”代表畸變模型的∏項和物理量)。對于基準(zhǔn)模型和畸變模型,僅有相似常數(shù)λd≠λL(t),其它各相似常數(shù)均為1時,縮比模型發(fā)生畸變,定義“板厚畸變系數(shù)”為 φ,根據(jù)文獻[9-11]有:
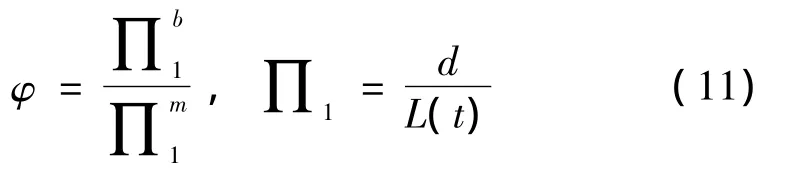
設(shè)畸變模型和基準(zhǔn)模型時間的因變∏項的比值為δt,稱之為“時間預(yù)測系數(shù)”。即:

時間預(yù)測系數(shù)δt僅是畸變系數(shù)φ的函數(shù),通過大量實驗測量或數(shù)值計算的方法可得到δt隨φ變化的規(guī)律,進而確定其函數(shù)形式和最終結(jié)構(gòu)畸變準(zhǔn)則。相關(guān)文獻表明[11],彈性體結(jié)構(gòu)基于該方法確定的畸變準(zhǔn)則進行畸變,得到的模型計算結(jié)果與基準(zhǔn)模型有很高的一致性,并且在制作工藝上的可控性好。
2 計算結(jié)果分析
為選定艦船總縱強度模型實驗的最優(yōu)方案,本文對四種艦船縮尺實驗方案進行水下爆炸數(shù)值計算分析,并對實際模型橫剖面彎矩預(yù)測偏差進行總結(jié),得到既能使實驗?zāi)P驮诠こ叹确秶鷥?nèi)實現(xiàn)對原型橫剖面彎矩的準(zhǔn)確預(yù)測,同時又滿足制造工藝的可控性和實驗成本的經(jīng)濟性的最終實驗方案。
2.1 模型實驗計算工況設(shè)定
本文以XXX艦有限元模型為原型,如圖1所示,選取攻擊武器為MDM-X型水雷,爆心位于船舯正下方,見圖2,裝藥質(zhì)量相當(dāng)于m=Wkg的TNT,調(diào)整爆距R=Z0m,使其氣泡周期[7]與船體濕模態(tài)一階固有頻率相同,使氣泡脈動載荷激起船體共振,探究XXX艦此典型工況下的總縱強度。
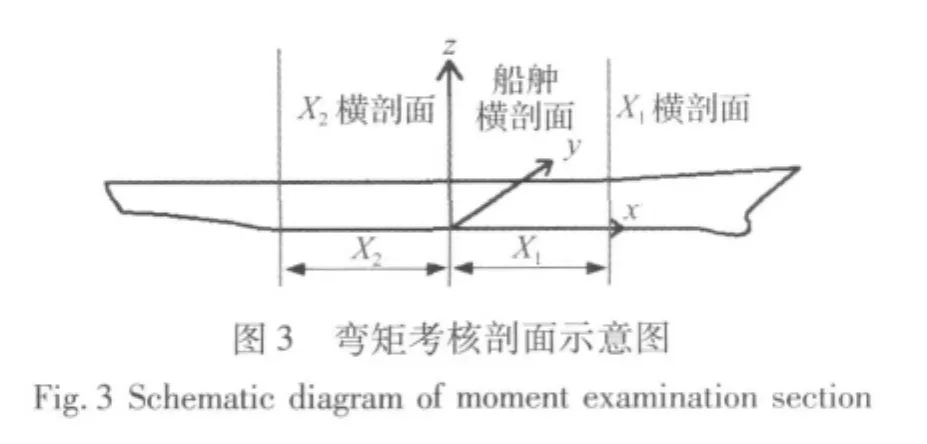
為了評估縮比模型與原模型的數(shù)值計算結(jié)果,本文選取了延船長方向上三處典型剖面部位進行橫剖面彎矩時歷曲線輸出,分別為船舯橫剖面、X1橫剖面、X2橫剖面,具體示意圖如圖3,其中X1=X2。


2.2 完全幾何相似模型實驗方案
為了選擇合適的縮尺比,本研究提出四種完全幾何縮比模型實驗方案與原型進行對比分析,采用自由場中水下爆炸一次沖擊波和氣泡脈動相似理論對模型進行相似加載,并考慮實驗?zāi)P偷慕?jīng)濟性及可操作性等因素,確定合適的縮比模型,為下一步畸變模型實驗方案做準(zhǔn)備。對上述艦船完全幾何縮小,艦船、藥包原型與縮比模型相似關(guān)系見表1,其中Dp為爆深D(m)處的水柱壓強,(D0)p=10.33 m為大氣壓的水柱壓強。
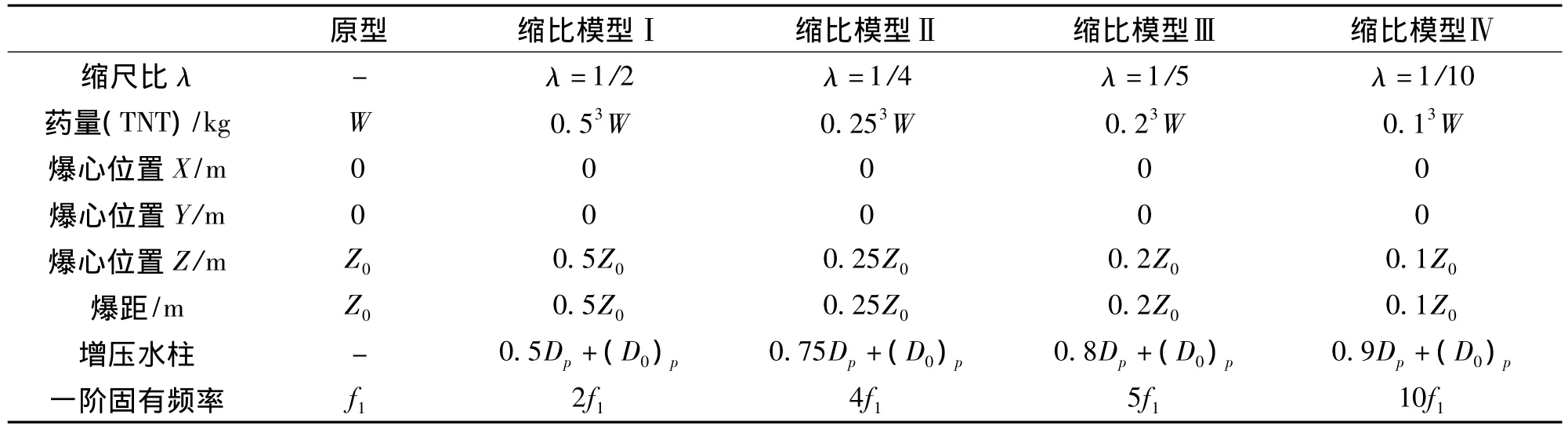
表1 XXX型艦原型與模型相似關(guān)系Tab.1 Similarity relation between the model and the archetype of XXX ship
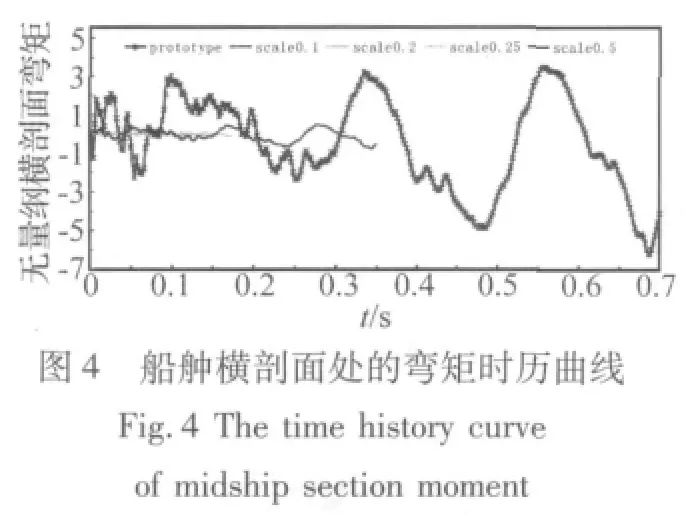
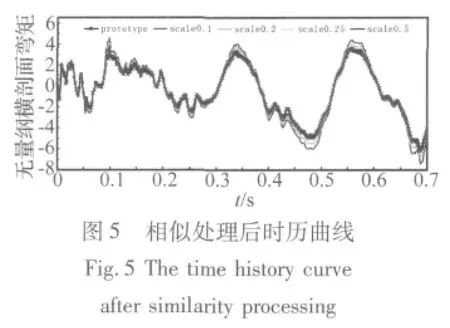
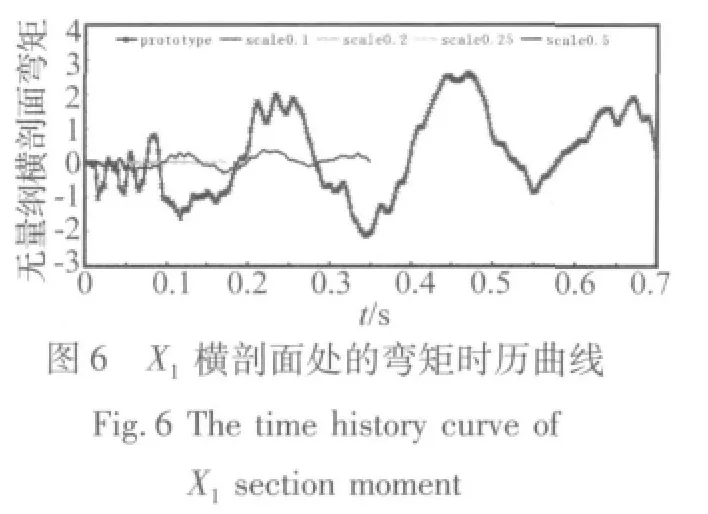
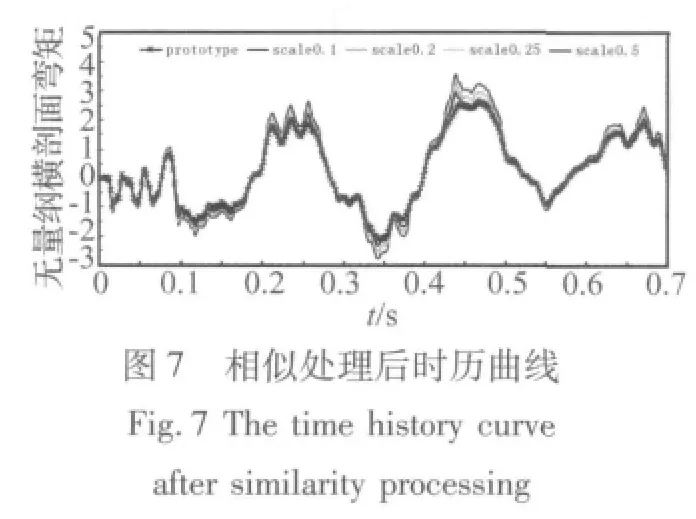
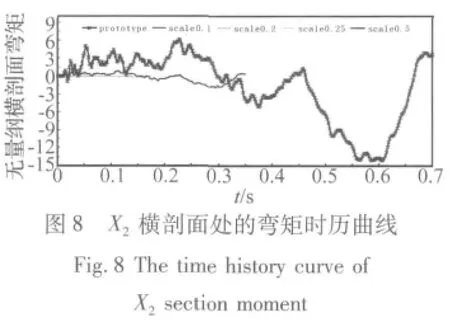

下面分別給出XXX艦及其縮比模型在靜水中遭受水下爆炸載荷作用時各個考核剖面的無量綱橫剖面彎矩時歷曲線。此處的原型與縮比模型彎矩時歷曲線由相應(yīng)剖面的輸出點擬合而得,將各模型時歷曲線的輸出點橫坐標(biāo)t按時間縮尺比放大,同時將各輸出點縱坐標(biāo)M按相應(yīng)的彎矩縮尺比放大,即得到相似處理后的模擬時歷曲線。無量綱橫剖面彎矩時歷曲線的原型與縮比模型相比,縮比模型的橫剖面彎矩縮尺比按特征長度相似常數(shù)三次方即換算,縮比模型的時間縮尺比按特征長度相似常數(shù)λl換算,相似處理后的時歷曲線結(jié)果如圖4~圖9(數(shù)據(jù)已經(jīng)過無量綱處理):
從上圖可以看出,應(yīng)用自由場中水下爆炸一次沖擊波和氣泡脈動相似理論處理后的縮比模型與原型的典型考核橫剖面彎矩時歷曲線基本吻合。應(yīng)用完全幾何相似模型,可以通過模型實驗非常準(zhǔn)確地預(yù)測原型結(jié)構(gòu)遭受水下爆炸載荷時的結(jié)構(gòu)響應(yīng)特性及其總縱強度。

2.3 畸變模型實驗方案
完全幾何相似模型中的板或梁的幾何尺寸(如厚度)按縮尺比進行縮尺時,會出現(xiàn)如焊接難度大、鋼材規(guī)格難以實現(xiàn)等問題,必須使用畸變模型。模型畸變后,圖3所考慮的考核剖面抗彎剛度必定發(fā)生變化,保證畸變模型預(yù)測精度的關(guān)鍵在于合理選取畸變系數(shù)φ,由前文推導(dǎo)可知,預(yù)測系數(shù)δt是畸變系數(shù)φ的函數(shù),但二者的函數(shù)形式并不確定,而且不同模型的畸變系數(shù)函數(shù)形式也不盡相同,實際上,預(yù)測系數(shù)δi與φ的函數(shù)關(guān)系可以通過一系列模型試驗來確定,但這樣做需要耗費大量的人力物力,顯然工程上是不可取的。因此,本文采用有限元預(yù)測系數(shù)法尋找預(yù)測系數(shù)δi隨畸變系數(shù)φ的變化規(guī)律。具體方案如下:首先定義完全幾何相似模型為基準(zhǔn)模型,以基準(zhǔn)模型為基礎(chǔ),僅對板厚進行畸變的模型定義為畸變模型,建立系列畸變模型和基準(zhǔn)模型之間的預(yù)測系數(shù)δi=F(φ)函數(shù)關(guān)系,結(jié)合完全幾何相似理論,實現(xiàn)對原型動響應(yīng)特性的預(yù)報。
數(shù)值實驗結(jié)果表明,當(dāng)畸變系數(shù)φ=3(板厚為3h的模型Model 4)時,畸變模型對原型的預(yù)測誤差最小。下面分別給出當(dāng)畸變系數(shù)φ=3時,XXX艦的基準(zhǔn)模型及各畸變模型的在靜水中遭受水下爆炸載荷作用無量綱橫剖面彎矩時歷曲線,及經(jīng)過相似處理的無量綱橫剖面彎矩時歷曲線對比圖。

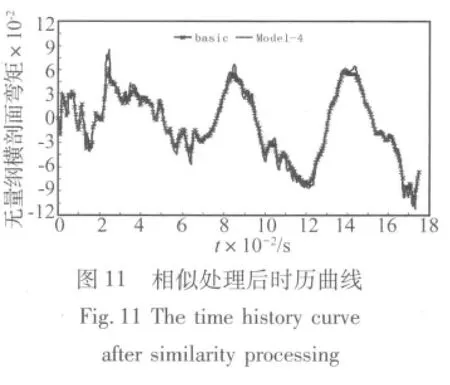
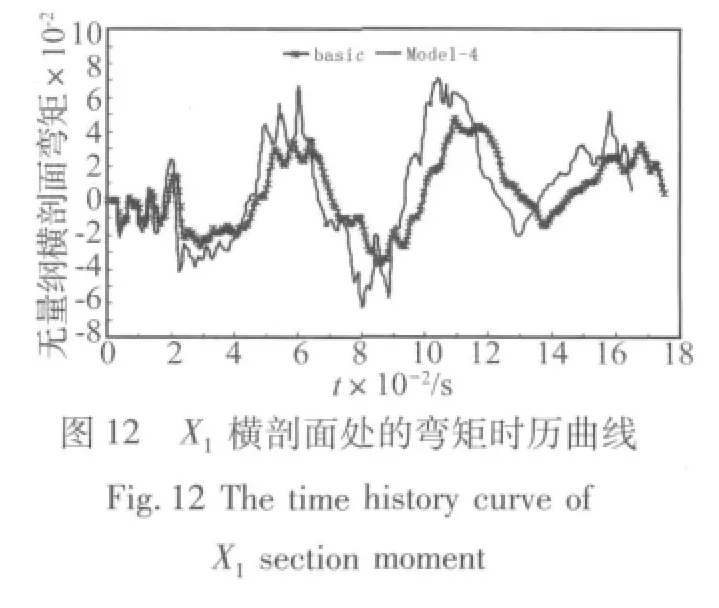

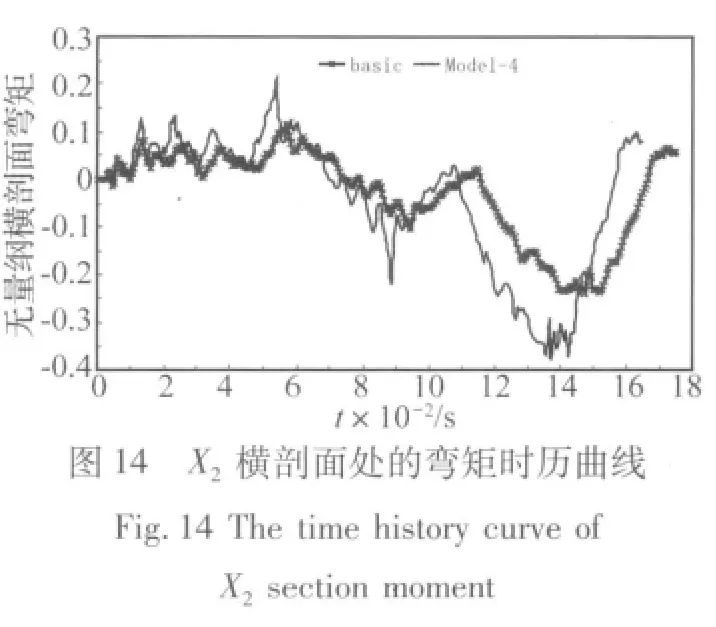

選取以上橫剖面的動響應(yīng)峰值進行預(yù)測偏差分析,見表2:
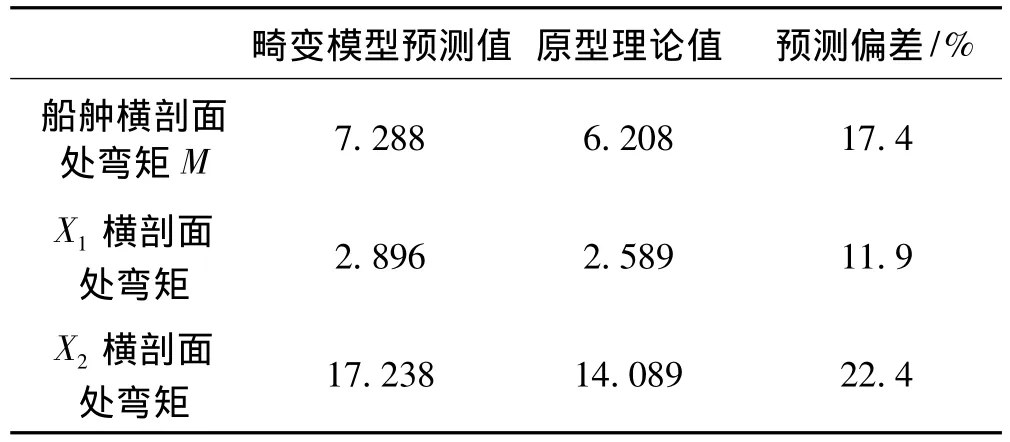
表2 典型部位彎矩峰值預(yù)測偏差分析Tab.2 Deviation analysis of moment peak of typical position

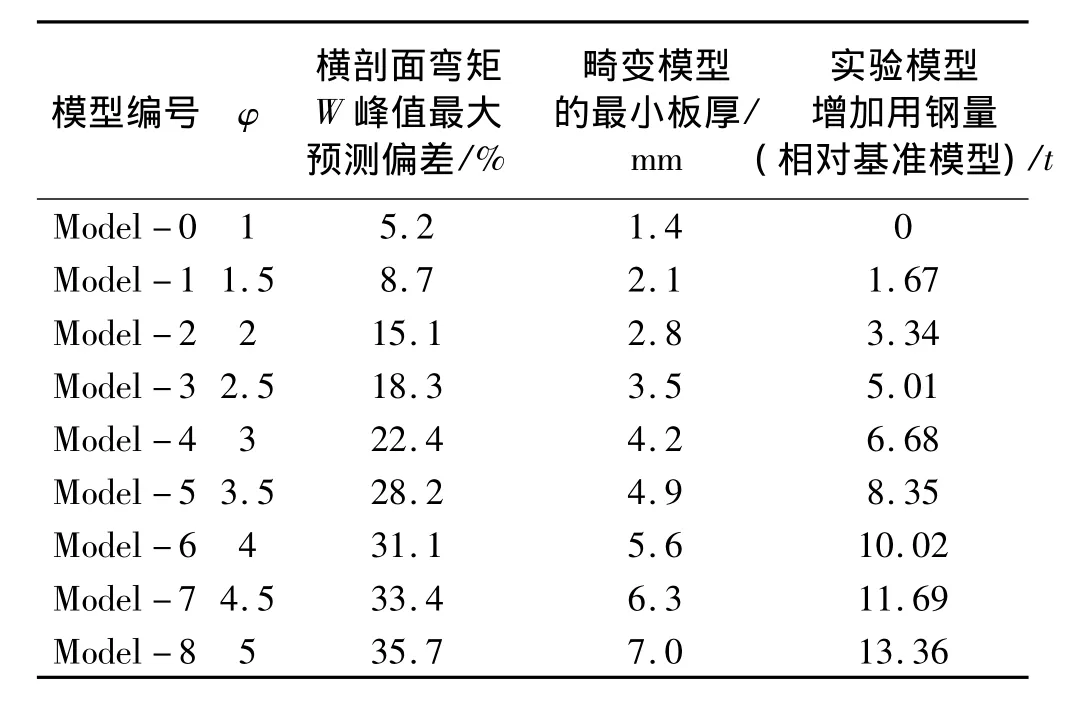
表3 畸變實驗?zāi)P驮u估表Tab.3 Evaluation table of distortion experimental model

3 結(jié)論
本文基于自由場中水下爆炸一次沖擊波和氣泡脈動相似律,通過數(shù)值實驗手段研究了在大縮尺比船模水下爆炸實驗中,使用畸變模型實現(xiàn)對原型總縱強度準(zhǔn)確預(yù)測的方法。通過對實驗結(jié)果的分析可得到的結(jié)論及建議如下:

(2)應(yīng)用完全幾何相似模型,可以通過模型實驗準(zhǔn)確地預(yù)測原型結(jié)構(gòu)遭受水下爆炸氣泡脈動載荷時的結(jié)構(gòu)響應(yīng)特性及其總縱強度。
[1]汪 玉.艦船現(xiàn)代沖擊理論及應(yīng)用[M].北京:科學(xué)出版社,2005:21-29.
[2]徐培譽.水下爆震對結(jié)構(gòu)之響應(yīng)[D].臺北:國立臺灣大學(xué),2004.
[3] Keil K A.The response of ship to underwater explosion[J].SNAME,1961,69(4):366-410.
[4]程素秋,寧永成,張 臣,等.相似理論在水下爆炸模型實驗中的應(yīng)用[J].船舶科學(xué)技術(shù),2008,30(3):96-99.
[5]張 亮,李云波.流體力學(xué)[M].哈爾濱:哈爾濱工程大學(xué)出版社,2007:179-187.
[6]張效慈.水下爆炸實驗相似準(zhǔn)則[J].船舶力學(xué),2007,2(1):108-118.
[7]庫爾P,羅耀杰,等譯.水下爆炸[M].北京:國防工業(yè)出版社,1960.
[8]Klaseboer E,Khoo B C,Hung K C.Dynamics of an oscillating bubble near a floating structure[J].Journal of Fluid and Structure,2005,21:395-412.
[9] Gel’fand B E,et al.Similarity criteria for underwater explosion[J].Combustion,Explosion,and Shock Waves,2004,40(2):214-218.
[10]徐 挺,著.相似方法及其應(yīng)用[M].北京:機械工程出版社,1995.
[11]謝建林.瞬態(tài)載荷作用下彈塑性結(jié)構(gòu)動響應(yīng)相似性研究[D].哈爾濱:哈爾濱工程大學(xué),2008:24-55.

