基礎會計教學中的數(shù)學思維

○ 林勇軍

（湖北經(jīng)濟學院 湖北 武漢 430205）

數(shù)學是科學家一致公認的、最具有美感的精密的自然科學。把一些數(shù)學思維引入到日常的會計教學中對于教學很有幫助，因為數(shù)學思維具有兩個無可比擬的優(yōu)點：一是高度的精確性，二是嚴密的邏輯性。由于數(shù)學思維固有的精確性優(yōu)點，運用數(shù)學方法可以準確地研究和描述一些數(shù)量關系。由于數(shù)學思維所固有的邏輯性，運用數(shù)學方法能嚴格遵循數(shù)理邏輯程序，從一定的前提必能得出確定的結(jié)論。筆者根據(jù)自己多年從事基礎會計（該課程在有些學校稱為“初級會計學”或“會計學原理”）課程教學的經(jīng)驗，對如何將數(shù)學思維貫穿到基礎會計教學中提出了一些見解。

一、發(fā)生額平衡法

試算平衡是根據(jù)各會計要素間的平衡關系來檢查各類賬戶的記錄是否正確的一種驗證方法。在檢查賬戶的記錄是否正確時我們需要編制“試算平衡表”，該表編制的時候主要采用兩種方法，一種是“發(fā)生額平衡法”，另一種是“余額平衡法”。采用發(fā)生額平衡法編制試算平衡表主要利用下列等式：

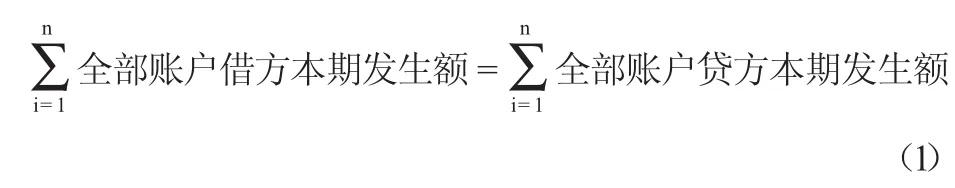
我們一般認為，當該等式成立，賬戶的登記基本正確；當該等式不成立，賬戶的登記一定有錯誤。但是有些學生會提出一些質(zhì)疑：“誰說賬戶登記正確了，該等式一定成立？”所以，我們必須先讓學生們相信：只要賬戶登記正確了，該等式一定成立。為證明該命題，我們就要運用數(shù)學中“等式的基本性質(zhì)”和歸納法。

1、等式的基本性質(zhì)

等式的兩邊都加上（或減去）同一個整式，等式仍舊成立（等式可以是一個數(shù)）。

2、歸納法

設p(n)是一個與正整數(shù)有關的命題，如果：

當 n=1 時，p(n)成立。

假設n=k（k≧1,k∈N）成立，由此推導出n=k+1時p(n)也成立。

根據(jù)以上可得出結(jié)論，對一切正整數(shù)n≧1，p(n)都成立。

下面，筆者舉例（見表1）來說明如何運用數(shù)學思維來解答學生們的提問。

證明：在這里，n表示第幾筆業(yè)務，p(n)表示等式（1）。

當n=1時，賬戶借方本期發(fā)生額=10000，賬戶貸方本期發(fā)生額=10000，顯然命題p(n)成立。

假設 n=k（k≧1,k∈N）時，p(n)也成立，此時有：

則當n=k+1時，由“等式的基本性質(zhì)”知上述等式的兩邊都加上800000時，等式仍舊成立。顯然此時有：

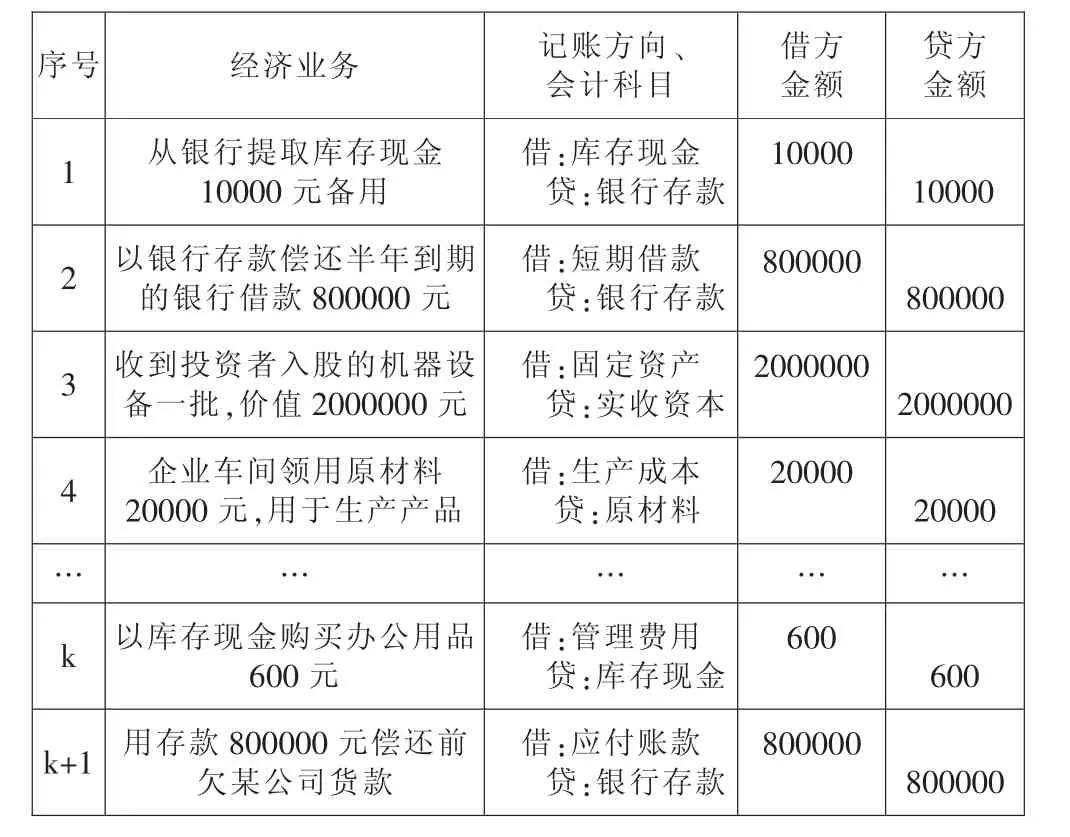
表1 經(jīng)濟業(yè)務及會計處理（單位：元）

即當n=k+1時p(n)也成立。

二、日記賬的登記依據(jù)

日記賬包括銀行存款日記賬和庫存現(xiàn)金日記賬，其中銀行存款日記賬的登記依據(jù)是銀行存款收款憑證（簡稱“銀收”）、銀行存款付款憑證（簡稱“銀付”）和庫存現(xiàn)金付款憑證（簡稱“現(xiàn)付”），現(xiàn)金日記賬的登記依據(jù)是庫存現(xiàn)金收款憑證（簡稱“現(xiàn)收”）、現(xiàn)付和銀付。通常情況下，教師只是通過對銀行存款日記賬和庫存現(xiàn)金日記賬的登記依據(jù)進行歸納總結(jié)，而沒有采用一些邏輯推理過程來加強學生的領悟和記憶。筆者在講課的過程中運用了數(shù)學當中的反證法完成了這一過程。

反證法所依據(jù)的是邏輯思維規(guī)律中的“矛盾律”和“排中律”。在同一思維過程中，兩個互相矛盾的判斷不能同時都為真，至少有一個是假的，這就是邏輯思維中的“矛盾律”；兩個互相矛盾的判斷不能同時都假，簡單地說“A或者非A”，這就是邏輯思維中的“排中律”。反證法在其證明過程中，得到矛盾的判斷，根據(jù)“矛盾律”，這些矛盾的判斷不能同時為真，必有一假，而已知條件、已知公理、定理、法則或者已經(jīng)證明為正確的命題都是真的，所以“否定的結(jié)論”必為假。再根據(jù)“排中律”，結(jié)論與“否定的結(jié)論”這一對立的互相否定的判斷不能同時為假，必有一真，于是我們得到原結(jié)論必為真。

筆者在這里僅說明“庫存現(xiàn)金日記賬”的登賬依據(jù)。庫存現(xiàn)金日記賬就是反映庫存現(xiàn)金的收支動態(tài)和庫存余額的賬簿，所以該賬簿所涉及的經(jīng)濟業(yè)務一定會引起庫存現(xiàn)金的變化，換句話來講，某憑證要想作為登記庫存現(xiàn)金日記賬的依據(jù)，它所反映的經(jīng)濟業(yè)務一定與庫存現(xiàn)金有關。大家知道，記賬憑證可分為現(xiàn)收、現(xiàn)付、銀收、銀付和轉(zhuǎn)賬憑證。轉(zhuǎn)賬憑證是用來記載不涉及庫存現(xiàn)金和銀行存款變化的業(yè)務，所以它記錄的經(jīng)濟業(yè)務一定不會被過到賬簿中去，即轉(zhuǎn)賬憑證肯定不能作為登記庫存現(xiàn)金日記賬的依據(jù)。現(xiàn)收和現(xiàn)付從名稱上看一定與現(xiàn)金有關，故一定能作為登記庫存現(xiàn)金日記賬的依據(jù)。現(xiàn)在只需要考察銀收與銀付了，在此我們借用數(shù)學中常用來證明命題的反證法。

其一，假設“銀收能作為登記庫存現(xiàn)金日記賬的依據(jù)”成立，考慮到銀收主要反映銀行存款的增加，則意味著銀收憑證中涉及的庫存現(xiàn)金一定減少，因此有：

如果我們單純考慮會計分錄（2），根據(jù)我們已掌握的知識“當涉及銀行存款和庫存現(xiàn)金間的相互劃轉(zhuǎn)業(yè)務時只填付款憑證”，則（2）應該編制現(xiàn)付憑證。這個結(jié)論和假設導致的“（2）出現(xiàn)在銀收中”相矛盾。所以，假設不成立，即銀收不能作為登記庫存現(xiàn)金日記賬的依據(jù)。

其二，假設“銀付能作為登記庫存現(xiàn)金日記賬的依據(jù)”成立，考慮到銀付主要反映銀行存款的減少，則意味著銀付憑證中涉及的庫存現(xiàn)金一定增加，因此有：

如果我們單純考慮會計分錄（3），根據(jù)我們已掌握的知識“當涉及銀行存款和庫存現(xiàn)金間的相互劃轉(zhuǎn)業(yè)務時只填付款憑證”，則（3）應該編制銀付憑證。該結(jié)論與假設導致的“（3）出現(xiàn)在銀付中”相吻合。所以，假設成立，即銀付能作為登記庫存現(xiàn)金日記賬的依據(jù)。

綜上所述，登記庫存現(xiàn)金日記賬的依據(jù)是：現(xiàn)收、現(xiàn)付和銀付。同理，可得出登記銀行存款日記賬的依據(jù)是：銀收、銀付和現(xiàn)付。

三、錯賬更正法的總結(jié)

錯賬更正法包括三種方法：劃線更正法、紅字更正法和補充登記法。在課堂上，我們分別講了該三種方法的各自適用情況、具體的更正步驟以及在更正時需要注意的問題。但是筆者發(fā)現(xiàn)，相當一部分學生連他們各自的適用情況都分辨不清楚，就更難說具體的更正了，對此，本文提出一個便于大家記憶的方法。

流程圖已成為高中數(shù)學必須掌握的一個知識要點，我們把由一些圖形符號和文字說明構(gòu)成，用來表示動態(tài)過程的圖示稱為流程圖。以下就是筆者利用構(gòu)建流程圖來幫助同學區(qū)分三種錯賬更正法的各自適用情況（見圖1）。

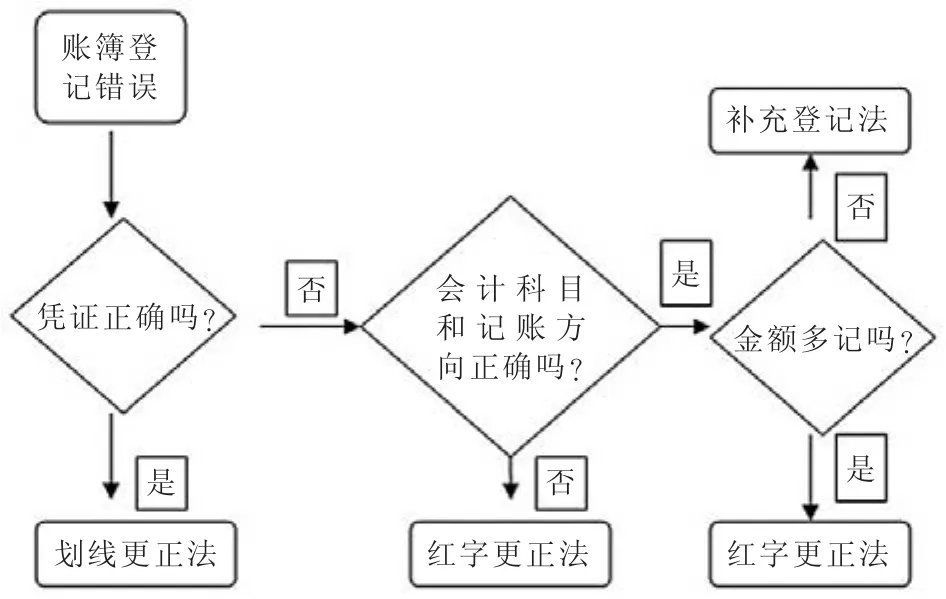
圖1 錯賬更正法適用情況流程圖

其實，在日常教學過程中，我們或多或少都已運用到數(shù)學思維來解決問題，但因為沒有書寫嚴格的邏輯推理過程，所以就漠視了數(shù)學思維在會計教學中的存在。筆者相信，只要用心，我們一定能在基礎會計學的教學過程中總結(jié)出更多的運用數(shù)學思維來解決會計教學問題的方法。

[1]劉尚林、楊明海：基礎會計學[M].中國市場出版社，2011（8）.

[2]仰恩大學會計系教改組：論成本會計學中的數(shù)學思維[J].學術問題研究，2008（1）.