三維高超聲速飛行器再入軌跡快速優化

劉鵬，趙吉松，谷良賢

(西北工業大學航天學院，陜西西安 710072)

引言

具有路徑約束和終端約束的三維高超聲速再入軌跡優化問題是一類復雜的最優控制問題。其求解方法主要分為間接法和直接法。間接法主要借助于變分法或龐特里亞金最大值原理(PMP)，把泛函優化轉化為哈密爾頓邊值問題(HBVP)。間接法具有優化精度高，滿足一階最優性必要條件等優點。但是，求解HBVP需要猜測無物理意義的協態變量，比較困難。傳統直接法把泛函優化轉化為非線性規劃問題(NLP)，降低了初值的敏感性，但存在計算量大、局部收斂、優化精度偏低等弊端。因此，采用傳統的間接法或直接法求解該類問題都存在很大困難。

近幾年，最優控制領域興起一類偽譜法。偽譜法屬于直接法，但具有全局收斂性，且在優化后的處理中能夠提供準確的協態變量，進而可驗證優化結果是否滿足一階最優性必要條件。偽譜法具有優化精度高、收斂快等優點。文獻［1］采用Legendre偽譜法求解了三維高超聲速再入軌跡最大橫程問題，并驗證了優化結果滿足一階最優性必要條件，但耗時7.5 min，而本文研究采用Gauss偽譜法求解該問題，精度相當，耗時僅7 s。

1 高超聲速再入軌跡優化問題描述

1.1 再入模型

設狀態向量為:x=［r，θ，φ，v，ψ，γ］，其中各元素分別為飛行器矢徑、經度、緯度、速度、航向角及彈道傾角，則飛行器的三自由度再入運動方程組［1］為:

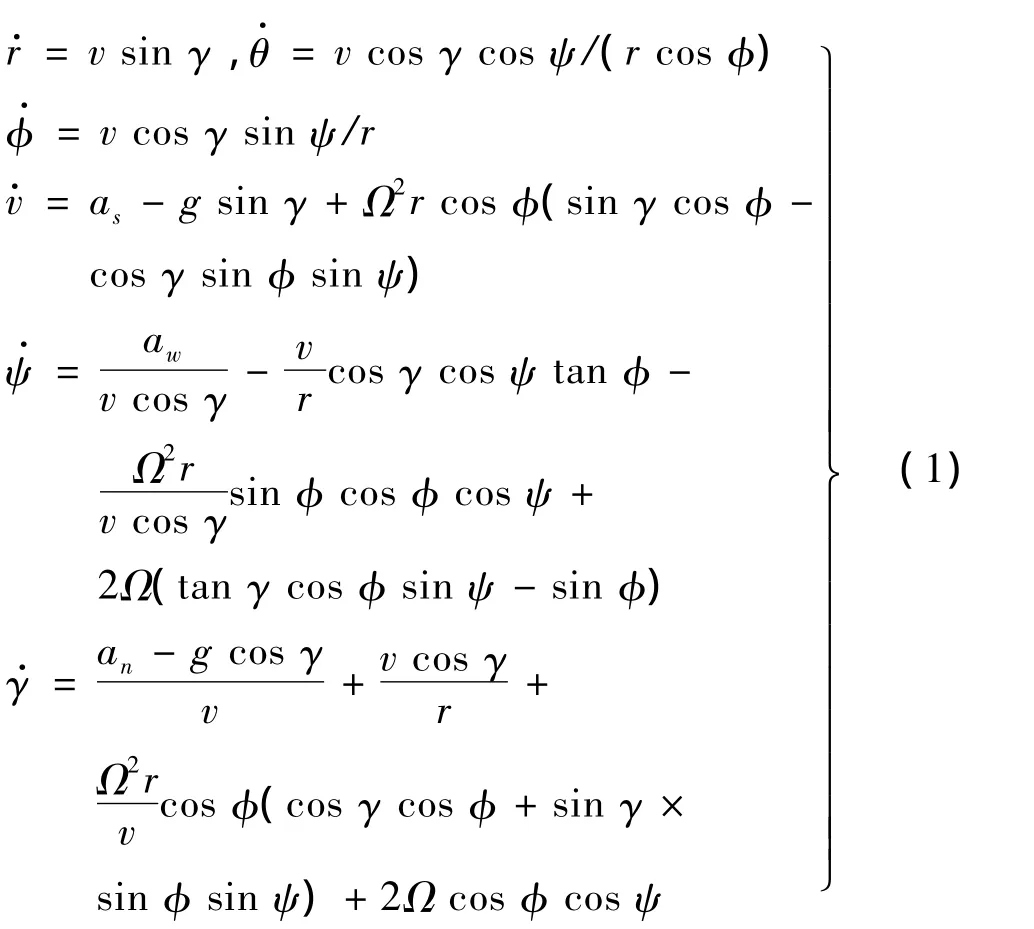
式中，g=μ/r2，μ=3.986 009×1014m3/s2;Ω為地球自轉角速度，Ω =7.272 2 ×10－5rad/s;as，an，aw分別為切向、法向及側向氣動力加速度，as=－D/m，an=L cosδ/m，aw=L sinδ/m，其中L和D分別為升力和阻力，δ為速度滾轉角，m為再入飛行器的質量，m=102 205 kg。其它參數的定義與取值參見文獻［1］。

1.2 再入軌跡優化問題

對于初始軌道為近赤道軌道再入彈道優化問題，橫向航程最大等價于終端緯度最大(φ＞0)或最小(φ＜0)。因此，本文的優化問題是求最優控制u(t)=［α(t)，δ(t)］T，使終端緯度

最小，并滿足微分方程約束式(1)，初始條件:h=rr0=79 248 m，v=7 334 m/s，φ =0°，θ=0°，ψ =0°，γ = －1.064°;終端條件:h=24 384 m，v=762 m/s，γ = －5°;氣動加熱邊界 qU=7.944 ×105W/m2。

2 偽譜方法簡介

偽譜方法基本思想是將積分區間離散化，在整個區間采用全局插值多項式逼近狀態變量，對插值多項式求導逼近狀態變量的導數，將微分方程約束、路徑約束等轉換為離散點處的代數約束，性能指標中的積分項由高代數精度的積分方法求取，從而將最優控制問題轉化為非線性規劃問題(NLP)。根據離散點的選取方法不同，偽譜方法可分為Legendre偽譜法(LPM)、Radau偽譜法(RPM)和Gauss偽譜法(GPM)等。目前，文獻［2-3］已證明了采用GPM離散最優控制問題得到的非線性規劃的KKT條件與最優控制問題的一階最優性必要性條件的離散形式之間的等價性。因此，本文采用了GPM求解最優軌跡。

2.1 Gauss偽譜法

根據性能指標的不同，最優控制問題可分為Mayer問題、Lagrange問題和Bolza問題，但三者可以相互轉化。以Bolza問題為例，求解最優控制u(t)∈Rm，使得如下目標函數取最小:

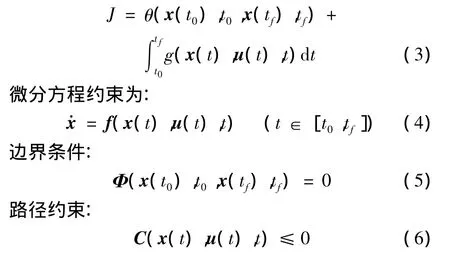
式中，x(t)∈Rn;θ∈R;g∈R;f∈Rn;Φ∈Rq;C∈Rc。

2.1.1區間變換

上述Bolza問題的積分區間是［t0，tf］，但偽譜法要求積分區間為［－1，1］。為此，通過下式將積分區間變換到［－1，1］:

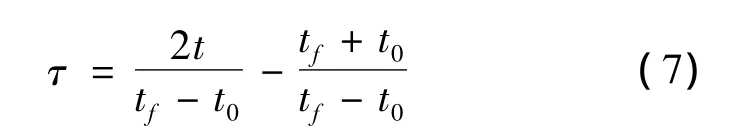
對于終端自由型最優控制問題，上式依然成立。變換后的Bolza問題的目標函數為:

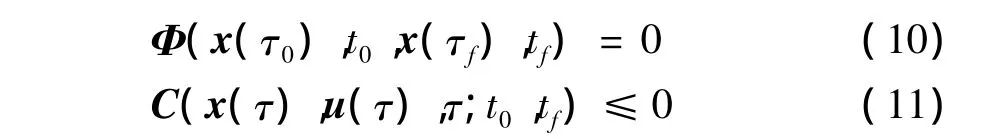
2.1.2 GPM 的離散方法

經過上述變換，GPM將最優控制問題轉化為NLP 問題:求離散點處的狀態變量 X(τi)，τi∈{τ0，τ1，…，τk，τf}，控制變量 U(τk)，τk∈{τ1，…，τk}，以及初始時刻t0和終端時刻tf(若終端自由)，使得性能指標式(19)最小化，并且滿足LG點處的微分方程約束式(15)、終端狀態約束式(17)、邊界條件約束式(10)和LG點處的路徑約束:

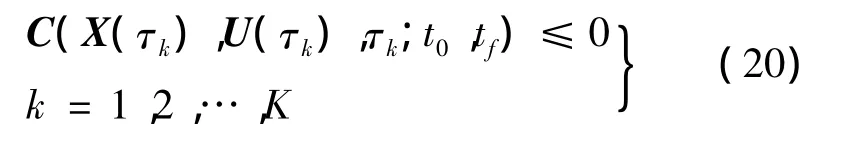
2.2 NLP求解方法

GPM將最優控制問題轉化為具有等式約束和不等式約束的NLP。直接由最優控制問題轉化得到的NLP各個變量、約束以及目標函數相差較大，難以收斂或者收斂緩慢。本文首先采用文獻［4］提出的歸一化方法處理NLP，然后采用SNOPT軟件包求解NLP［5］。SNOPT采用稀疏序列二次規劃算法(Sequential Quadratic Programming，SQP)，通過求解線性化約束條件下的二次規劃子問題獲得每一步的搜索方向。對于大規模問題，當只有部分變量表現出非線性或變量的自由度較少(多數約束處于激活狀態)時，SNOPT非常有效。SNOPT對目標函數和約束條件的計算次數較少，適用于求解目標函數和約束條件及其雅克比矩陣的計算量較大的問題。由最優控制問題轉化得到的NLP為稀疏問題，存在一直處于“激活”狀態的等式約束等，并且目標函數和約束條件的計算量較大，適合采用SNOPT求解。

2.3 協態變量映射

盡管間接法存在推導復雜、HBVP難以求解等弊端，但其有著堅實的理論基礎(變分法及Pontryagin最小值原理)，優化精度高，并且優化結果滿足一階最優性必要條件。HBVP求解困難的主要原因是協態變量的難以求解。因此，通過直接法的優化結果確定協態變量對判斷解的最優性有重要意義。對于GPM，文獻［3］推導出可通過下式求解協態變量。

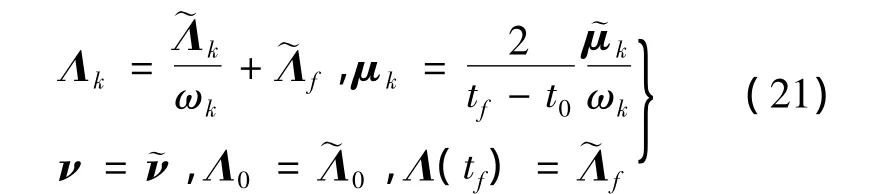
3 優化結果及其分析

采用40階的Legendre多項式求解該問題，狀態量初值按初始狀態與終端狀態進行線性插值，控制變量初值取［25°，45°］T，終端時間初值取 2 000 s。在Matlab平臺下，工作站HP XW9300(CPU AMD 2.59 GHz)耗時約7 s，最優解φ(tf)= －28.750 05°。圖1為最優軌跡狀態變量變化曲線。圖中，圓圈為GPM的離散解，實線為采用Matlab ode45優化得出的最優控制的積分結果。

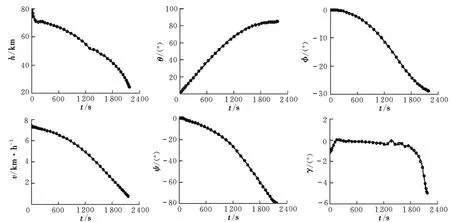
圖1 最優再入軌跡狀態量變化曲線

ode45積分結果與目標終端狀態的誤差分別為:高度1.628 5 m(0.006 7%)，速度0.103 9 m/s(0.013 6%)，彈道傾角0.002 8°(0.056 3%)。圖2為最優控制變化曲線，圖中圓圈為GPM的離散解，實線為Lagrange插值得出的結果。圖3為Hamiltonian沿最優軌跡變化歷程(注意縱坐標單位)。算例為終端時間自由型自治系統，由間接法可知，Hamiltonian應為0。可見，GPM的優化結果能夠很好地滿足一階最優性必要條件。圖4為氣動加熱率沿最優軌跡的變化過程。為了對比，圖中給出了不受約束的氣動加熱率變化情況(其它條件相同)。文獻［1］達到類似優化精度需要80個節點，耗時7.5 min(CPU Pentium Ⅳ1.8 GHz，內存512 MB)。

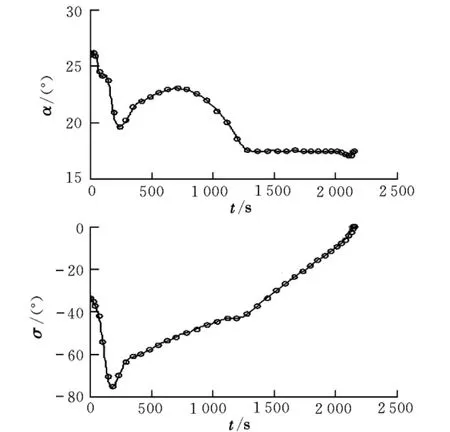
圖2 最優控制變化曲線

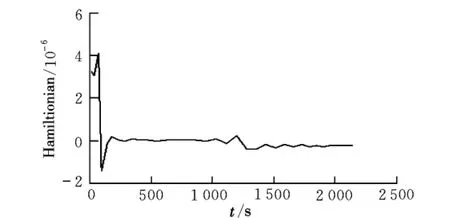
圖3 Hamiltonian沿最優軌跡變化曲線

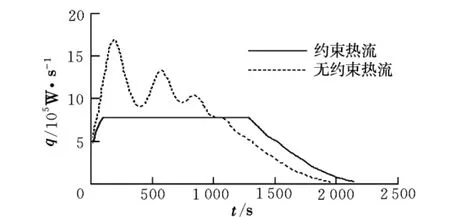
圖4 氣動加熱率變化曲線

4 結束語

本文采用GPM求解了三維高超聲速再入軌跡的最大橫程問題。算例中，GPM耗時約7 s即可生成一條嚴格滿足各種約束的三維最優再入軌跡，具有在線優化的潛力，并且優化精度高，滿足一階最優性必要條件。需要說明的是，本文基于解析形式的氣動模型，對于非解析形式的氣動模型，理論上可通過數值微分求取導數，但這樣會使機時迅速增加。因此，需要研究如何采用GPM快速求解非解析氣動模型的軌跡優化問題。

［1］ Scott Josselyn，Ross IM.Rapid verificationmethod for the trajectory optimation of reentry vehicles［J］.Journal Guidance:Engineering Notes，2002，26(3):505-508.

［2］ Benson D.A Gauss pseudospectral transcription for optimal control［D］.Boston，CA，US:Massachusetts Institute of Technology，2004.

［3］ Huntington G T.Advancement and analysis of a Gauss pseudospectral transcription for optimal control problems［D］.Boston，CA，US:Massachusetts Institute of Technology，2007.

［4］ Betts JT.Practicalmethods for optimal control using nonlinear programm ing［M］.Philadelphia:SIAM Press，2001.

［5］ Gill P E，Murray W，Saunders M A.SNOPT:a SQP algorithm for large-scale constrained optimization［J］.SIAM Journal on Optimization，2002，12(4):979-1006.