多元智能理論在護(hù)理臨床實(shí)習(xí)教學(xué)中的應(yīng)用研究
韓斗玲呂金菊曾等娣
(1.九江學(xué)院護(hù)理學(xué)院,江西九江332000;2.九江學(xué)院附屬醫(yī)院)
·教與學(xué)·
多元智能理論在護(hù)理臨床實(shí)習(xí)教學(xué)中的應(yīng)用研究
韓斗玲1呂金菊2曾等娣2
(1.九江學(xué)院護(hù)理學(xué)院,江西九江332000;2.九江學(xué)院附屬醫(yī)院)
目的探討護(hù)理臨床實(shí)習(xí)教學(xué)中應(yīng)用多元智能理論的效果。方法將我校護(hù)理學(xué)院在附院實(shí)習(xí)的2008屆、2009屆護(hù)生分為兩組,其中,2008屆為對照組,2009屆為實(shí)驗(yàn)組。實(shí)驗(yàn)組采用傳統(tǒng)教學(xué)法和以多元智能理論為指導(dǎo)的教學(xué)模式;對照組采用傳統(tǒng)教學(xué)方法。教學(xué)評價(jià)采用考試和問卷調(diào)查。結(jié)果實(shí)驗(yàn)組與對照組學(xué)生理論考試成績比較,差異無顯著意義(P>0.05);技能操作考試、綜合能力考核成績比較,差異有極顯著意義(P<0.01);問卷調(diào)查結(jié)果,認(rèn)為該教學(xué)模式很好和較好的學(xué)生為82.35%。結(jié)論多元智能理論應(yīng)用于護(hù)理臨床實(shí)習(xí)教學(xué),提高了教學(xué)效果,有利于學(xué)生綜合素質(zhì)的提高。為了更客觀的評價(jià)教學(xué)效果,真實(shí)反映學(xué)生的智能水平,需建立多元化的護(hù)理臨床實(shí)習(xí)教學(xué)評價(jià)新體系。
多元智能理論 臨床教學(xué) 護(hù)理專業(yè) 實(shí)習(xí)生
美國心理學(xué)家霍華德·加德納針對傳統(tǒng)智能一元理論提出了多元智能理論,指出了人類思維和認(rèn)識(shí)世界的方式是多元化的。加德納認(rèn)為人的智能至少包括語言智能、數(shù)理邏輯智能、視覺空間智能、音樂節(jié)奏智能、身體運(yùn)動(dòng)智能、人際交往智能、自我認(rèn)識(shí)智能和自然觀察智能等八個(gè)方面[1]。多元智能結(jié)構(gòu)的確立,為我們在教學(xué)中如何開發(fā)學(xué)生的智能潛能、提高綜合素質(zhì)提供了理論依據(jù)。護(hù)生臨床實(shí)習(xí)是護(hù)理學(xué)專業(yè)教學(xué)過程中極為重要的階段,在臨床教學(xué)中如何使護(hù)生獲得全面發(fā)展,為畢業(yè)后能在各級醫(yī)療衛(wèi)生保健機(jī)構(gòu)中從事護(hù)理工作打好堅(jiān)實(shí)基礎(chǔ),一直是護(hù)理界共同關(guān)心的熱點(diǎn)問題之一。為探討更佳的護(hù)理臨床實(shí)習(xí)教學(xué)模式,我們嘗試將多元智能理論應(yīng)用于護(hù)理臨床實(shí)習(xí)教學(xué)中,根據(jù)學(xué)生的智能特點(diǎn)因材施教,取得了較好效果。
1 對象與方法
1.1 對象 采用回顧性分析法將我校護(hù)理學(xué)院在附院實(shí)習(xí)的2008屆、2009屆護(hù)生分為兩組,其中, 2009屆為實(shí)驗(yàn)組,2008屆為對照組。在實(shí)驗(yàn)組34人中,女28人,男6人;對照組31人中,女27人,男4人,兩組護(hù)生的年齡均為19~22歲。兩組學(xué)生在校各課程成績比較差異無顯著意義(P>0.05)。
1.2 方法
1.2.1 教學(xué)方法
1.2.1.1 對照組 采用傳統(tǒng)的護(hù)理臨床教學(xué)方法。按護(hù)理學(xué)院制訂的實(shí)習(xí)大綱和手冊,結(jié)合醫(yī)院護(hù)理部的實(shí)習(xí)帶教計(jì)劃進(jìn)行教學(xué)。
1.2.1.2 實(shí)驗(yàn)組 在傳統(tǒng)護(hù)理臨床教學(xué)方法的基礎(chǔ)上,應(yīng)用多元智能理論的理念,根據(jù)護(hù)理學(xué)院提供的每位護(hù)生背景、學(xué)習(xí)成績、智能特點(diǎn)、興趣特長等資料,將對學(xué)生的多元智能培養(yǎng)與臨床實(shí)習(xí)教學(xué)各環(huán)節(jié)相結(jié)合,創(chuàng)建多元化的教學(xué)環(huán)境,采用多元化的教學(xué)方法,從多維的角度開發(fā)學(xué)生的智能,促進(jìn)學(xué)生全面發(fā)展。具體培養(yǎng)內(nèi)容為:(1)語言智能培養(yǎng) 根據(jù)學(xué)生的認(rèn)知規(guī)律,在已有知識(shí)的基礎(chǔ)上加強(qiáng)護(hù)理操作、護(hù)理評估、健康教育、病案討論、護(hù)理文件記錄等過程的語言智能培養(yǎng)。教學(xué)中,鼓勵(lì)學(xué)生主動(dòng)表達(dá)自己的想法,通過討論交流思想,啟迪智慧,解決自己的問題,達(dá)到逐步發(fā)展語言智能及運(yùn)用語言的能力;(2)視覺空間智能培養(yǎng) 各帶教科室根據(jù)專科特點(diǎn),利用多媒體與床邊教學(xué)相結(jié)合的方法,展現(xiàn)各專科疾病的護(hù)理知識(shí),護(hù)理操作技能。通過直觀性與形象性的教學(xué),提高學(xué)生的觀察能力、形象思維能力和實(shí)踐能力;(3)數(shù)理邏輯智能培養(yǎng) 數(shù)理邏輯智能最核心的是發(fā)現(xiàn)問題和解決問題的能力。帶教老師有意識(shí)培養(yǎng)學(xué)生利用各種感官(視、聽、嗅、觸覺)及輔助工具獲取患者的病情信息,指導(dǎo)學(xué)生運(yùn)用邏輯思維綜合分析,及時(shí)發(fā)現(xiàn)患者存在的護(hù)理問題,提出護(hù)理診斷,制定并落實(shí)護(hù)理措施,將在校所學(xué)的陳述性知識(shí)轉(zhuǎn)化為臨床的程序性知識(shí),形成統(tǒng)一而不零散的知識(shí)結(jié)構(gòu);(4)身體運(yùn)動(dòng)智能培養(yǎng) 護(hù)理操作技能教學(xué)中,強(qiáng)調(diào)操作的科學(xué)性、準(zhǔn)確性和規(guī)范性。運(yùn)用角色轉(zhuǎn)換、情境教學(xué)、實(shí)踐反思等方法,反復(fù)訓(xùn)練,使學(xué)生對每一技能操作達(dá)到動(dòng)作準(zhǔn)確、靈活、協(xié)調(diào)和嫻熟,以體現(xiàn)護(hù)理操作美、護(hù)士行為美;(5)人際關(guān)系技能培養(yǎng) 采用小組合作學(xué)習(xí)的模式,加強(qiáng)學(xué)生之間、學(xué)生與老師、學(xué)生與患者的互動(dòng)和交流,使學(xué)生在互幫、互助、合作的氛圍中共同學(xué)習(xí)、進(jìn)步,培養(yǎng)團(tuán)隊(duì)協(xié)作精神,提高人際溝通技巧與組織管理能力;(6)自我認(rèn)識(shí)智能的培養(yǎng) 幫助學(xué)生認(rèn)識(shí)自己在知識(shí)理解和技能掌握方面存在的偏差,激勵(lì)學(xué)生改進(jìn);指導(dǎo)學(xué)生對所學(xué)知識(shí)舉一反三,及時(shí)糾正學(xué)生在護(hù)理活動(dòng)過程中存在的缺陷。
1.2.2 評價(jià)方法
1.2.2.1 實(shí)習(xí)成績評定 包括理論、操作技能與綜合能力考試三部分,理論考試成績?yōu)閷?shí)習(xí)期間兩次理論考試總評分,操作技能、綜合能力考試成績?yōu)楦鲗?shí)習(xí)科室成績總評分。(1)理論考試:實(shí)習(xí)中期和結(jié)束時(shí),兩組學(xué)生采用相同題型和難易度的試卷進(jìn)行理論考試,試卷滿分為100分;(2)操作技能考核:各科實(shí)習(xí)結(jié)束時(shí),按實(shí)習(xí)大綱要求選擇1項(xiàng)護(hù)理操作技術(shù)進(jìn)行考核,滿分為100分;(3)綜合能力考試:各科實(shí)習(xí)結(jié)束時(shí),選擇典型臨床病例,按護(hù)理程序進(jìn)行,考核點(diǎn)包括理論知識(shí)、專科護(hù)理技能、溝通能力和綜合分析問題能力,滿分為100分。
1.2.2.2 問卷調(diào)查 實(shí)習(xí)結(jié)束時(shí),對實(shí)驗(yàn)組34名學(xué)生進(jìn)行問卷調(diào)查,共收回有效問卷34份,回收率為100%。
1.2.3 統(tǒng)計(jì)學(xué)方法 所有數(shù)據(jù)均輸入計(jì)算機(jī),計(jì)量數(shù)據(jù)采用±s表示,計(jì)數(shù)資料采用率(%)表示,運(yùn)用SAS 9.2統(tǒng)計(jì)分析軟件包進(jìn)行數(shù)據(jù)處理,以 P< 0.05為差異有顯著意義。
2 結(jié)果
2.1 兩組學(xué)生實(shí)習(xí)成績比較(表1)
表1 兩組學(xué)生實(shí)習(xí)成績比較 (分,±s)
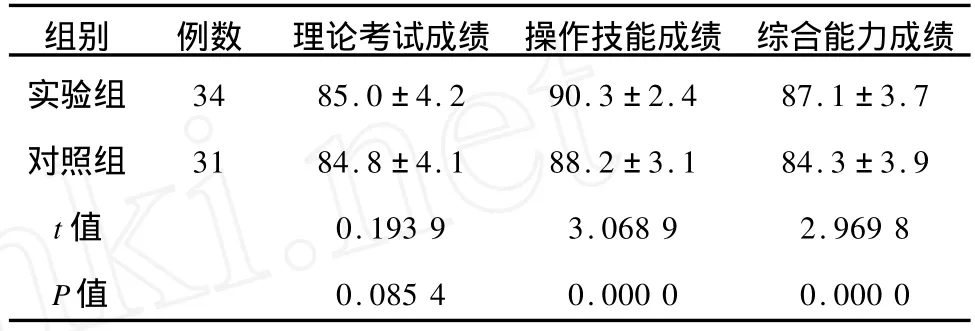
表1 兩組學(xué)生實(shí)習(xí)成績比較 (分,±s)
組別 例數(shù) 理論考試成績 操作技能成績 綜合能力成績實(shí)驗(yàn)組 34 85.0±4.2 90.3±2.4 87.1±3.7對照組 31 84.8±4.1 88.2±3.1 84.3±3.9 t值 0.193 9 3.068 9 2.969 8 P值 0.085 4 0.000 0 0.000 0
2.2 對實(shí)驗(yàn)組學(xué)生問卷調(diào)查結(jié)果(表2)

表2 實(shí)驗(yàn)組學(xué)生對臨床實(shí)習(xí)效果評價(jià) n(%)
3 討論
3.1 對學(xué)生多元智能培養(yǎng)是素質(zhì)教育的要求 多元智能理論以其豐富的教育內(nèi)涵,成為我國素質(zhì)教育改革的重要理論指導(dǎo),為高校教學(xué)實(shí)踐提供了新的思路。多元智能理論告訴我們,教育的主要目的不僅在于知識(shí)的傳授,更在于發(fā)掘并指引學(xué)生智力的發(fā)展。教學(xué)中沒有學(xué)生的主體地位,學(xué)生的發(fā)展也就無從談起[2]。因此,要樹立“以學(xué)生為本”的教育理念,把學(xué)生的發(fā)展放在中心位置。我們應(yīng)從多維的角度看待學(xué)生的智力,重視環(huán)境和教育對學(xué)生智力發(fā)展的影響與制約,最大限度地開發(fā)學(xué)生的多種智能和潛能。傳統(tǒng)的護(hù)理實(shí)習(xí)教學(xué),依據(jù)實(shí)習(xí)大綱、手冊和帶教計(jì)劃進(jìn)行教學(xué),帶教老師只能針對大多數(shù)學(xué)生能理解的水平,通過講授和操作演示來傳遞教學(xué)內(nèi)容和知識(shí),未兼顧到護(hù)生在知識(shí)背景、智能特點(diǎn)、學(xué)習(xí)方法、接受能力等方面的差異。護(hù)生處于被動(dòng)接受的地位,學(xué)習(xí)興趣、學(xué)習(xí)能力不能充分發(fā)揮,限制了創(chuàng)新能力的發(fā)展,不利于學(xué)生的智能開發(fā)。因此,傳統(tǒng)的護(hù)理臨床教學(xué)模式不能滿足學(xué)生持續(xù)性發(fā)展的需要。
3.2 對護(hù)生多元智能培養(yǎng)是培養(yǎng)護(hù)理人才的需要隨著社會(huì)和現(xiàn)代科技的發(fā)展,社會(huì)對護(hù)理服務(wù)的要求發(fā)生了改變。護(hù)生僅具有扎實(shí)的護(hù)理專業(yè)知識(shí)及技能已不能滿足社會(huì)需求,還需具有廣博的人文學(xué)科知識(shí),具備人際溝通、思維、管理組織等能力[3]。
因此,我們積極探索護(hù)理臨床教學(xué)新模式,以多元智能理論指導(dǎo)教學(xué),積極營造有利于護(hù)生多元智能培養(yǎng)的教學(xué)環(huán)境,在培養(yǎng)學(xué)生掌握扎實(shí)理論知識(shí)和實(shí)踐技能的同時(shí),充分考慮學(xué)生智能的差異性,因材施教,運(yùn)用多元化的教學(xué)策略,發(fā)展學(xué)生獨(dú)立獲取知識(shí)的能力、人際溝通能力、臨床思維能力及創(chuàng)新能力。
3.3 多元智能理論為指導(dǎo)的教學(xué)模式提高了臨床教學(xué)效果 研究結(jié)果表明,實(shí)驗(yàn)組與對照組學(xué)生理論考試成績比較,差異無顯著意義(P>0.05);技能操作、綜合能力考試成績比較,差異有極顯著性意義(P<0.01),說明實(shí)施多元智能理論為指導(dǎo)的教學(xué)模式后,實(shí)驗(yàn)組學(xué)生綜合能力有顯著提高。分析其原因:(1)多元化的教學(xué)能激發(fā)學(xué)生學(xué)習(xí)的主動(dòng)性和積極性。教師在了解護(hù)生背景、學(xué)習(xí)成績、智能特點(diǎn)、興趣特長等信息后,針對不同智能特點(diǎn),采取相應(yīng)的教學(xué)活動(dòng)和方法,實(shí)現(xiàn)個(gè)性教育和差異教育,從而開發(fā)了每位學(xué)生的優(yōu)勢智力領(lǐng)域,提高了學(xué)習(xí)興趣。如“以臨床病例為引導(dǎo)”的教學(xué)活動(dòng),學(xué)生通過收集患者的健康資料,開展小組討論,提出問題,制定措施,促使學(xué)生積極運(yùn)用所學(xué)理論知識(shí)不斷的思考、綜合分析,從而產(chǎn)生了強(qiáng)烈的內(nèi)在學(xué)習(xí)動(dòng)機(jī),激發(fā)學(xué)生求知欲和學(xué)習(xí)興趣,調(diào)動(dòng)了學(xué)習(xí)的主動(dòng)性和積極性;(2)有利于學(xué)生能力和綜合素質(zhì)的提高。教學(xué)中,一方面把講解、討論和實(shí)踐結(jié)合起來,為護(hù)生提供一個(gè)綜合性的臨床訓(xùn)練機(jī)會(huì),要求學(xué)生應(yīng)用護(hù)理程序,結(jié)合實(shí)例,圍繞問題進(jìn)行推理、分析,并引導(dǎo)學(xué)生尋找解決問題的途徑和方案,較好地培養(yǎng)和鍛煉了學(xué)生的思維能力、綜合分析能力及解決問題的能力。另一方面,在以小組學(xué)習(xí)的合作性團(tuán)隊(duì)中,學(xué)生具有不同的知識(shí)結(jié)構(gòu)、智慧水平、思維和認(rèn)知方式,可以互相交流、啟發(fā),使學(xué)習(xí)的獨(dú)立性、創(chuàng)造性得到相應(yīng)的發(fā)展,同時(shí)也提高了團(tuán)隊(duì)協(xié)作精神和交流溝通技巧。
3.4 建立多元化的護(hù)理臨床實(shí)習(xí)教學(xué)評價(jià)體系多元智能理論主張教學(xué)評價(jià)要注重情景性、發(fā)展性、多元性和獨(dú)特性[4]。對學(xué)生的評價(jià)應(yīng)以促進(jìn)學(xué)生的發(fā)展為根本目的,應(yīng)對其學(xué)習(xí)過程中展示的各種智能及在各個(gè)智能領(lǐng)域的發(fā)展,采取多渠道多方面進(jìn)行評價(jià)。可從以下方面對舊的評價(jià)體系進(jìn)行修正: (1)評估主體的多元化,變單純由教師評價(jià)為學(xué)生、教師共同評價(jià),自主評價(jià)與集體評價(jià)相結(jié)合;(2)在評價(jià)內(nèi)容上,不僅僅評價(jià)考試所要求的書本上的語言知識(shí),而應(yīng)全面地評價(jià)學(xué)生的各種素質(zhì)和能力; (3)評價(jià)手段除常用的考試和測驗(yàn)外,還可采取如口頭評價(jià)、實(shí)地評價(jià)、觀測評價(jià)等手段;(4)重視評價(jià)的情景化,使評價(jià)與學(xué)習(xí)融為一體,成為學(xué)習(xí)的一部分,能真實(shí)地展現(xiàn)學(xué)生的認(rèn)知水平,發(fā)現(xiàn)學(xué)生的智能強(qiáng)項(xiàng)和潛力,為今后實(shí)施更有效的教學(xué)提供參考。
[1] 霍華德·加德納.多元智能[M].第2版.北京:新華出版社, 2003:1-9.
[2] 韓斗玲.“自主—合作”模式在基礎(chǔ)護(hù)理學(xué)教學(xué)中的應(yīng)用[J].教育與職業(yè),2009,(27):88-89.
[3] 劉義蘭,王桂蘭,趙光紅.現(xiàn)代護(hù)理教育[M].北京:中國協(xié)和醫(yī)科大學(xué)出版社,2002:1-11.
[4] 戴冬梅,高洪濤.多元智能理論在實(shí)驗(yàn)教學(xué)中的探索[J].實(shí)驗(yàn)室研究與探索,2007,26(12):101-102.
R471
A
1002-6975(2010)13-1184-03
2009-12-30)
韓斗玲(1963-),女,江西九江,本科,副教授,教研室主任,從事護(hù)理教育工作
KeywordsTheo ry of multip le intelligences Clinical teaching Nursing Intern

