柔性臂空間機器人的一類運動學方程及軌跡規劃

夏長俊，顧文錦，楊秀霞

（海軍航空工程學院 a．飛行器工程系；b．控制工程系，山東 煙臺 264001）

大型、輕質柔性臂空間機器人可以降低發射成本，增大機械臂操作的有效負載；同時增大了機械臂的操作空間，使空間機器人可以在更加廣闊的太空空間內作業。但是，大型柔性臂空間機器人在進行空間作業時，機械臂結構會發生惱人的低頻振動，給空間機械臂定位以及運動規劃帶來很多困難。在空間機器人領域的研究大多是針對剛性臂空間機器人的，不考慮機械臂臂桿柔性對空間機器人作業任務的影響。在剛性臂空間機器人運動學建模方面，Z.Vafa 和S.Dubowsky[1]提出了虛擬機械臂VM(Virtual Manipulator)的概念；Y.Umetani 和K.Yoshida[2]根據線動量守恒和角動量守恒方程，提出了反映空間機器人工作空間與關節空間運動速度關系的廣義雅可比矩陣 GJM(Generalized Jacobian Matrix)；K.Yamada 和 K.Tsuchiya[3]，R.Mukherjee 和 Y.Nakamura[4]，Y.Yokokohji 和T.Toyoshima[5]等人采用不同的方法推導出GJM；GJM 成功地用于空間機器人的分解速度控制以及轉置雅可比控制，已經成為描述空間機器人運動的重要理論基礎。在空間機器人軌跡規劃方面，T.Suzuki 和Y.Nakamura[6]提出空間機器人螺旋運動路徑規劃方法；Y.Nakamura 和R.Mukherjee[7]對自由漂浮空間機器人系統的非完整動力學性質作了分析和利用，并應用Lyapunov 方法進行機械臂關節空間的路徑規劃。對剛性臂空間機器人的運動學建模以及軌跡規劃問題的研究，都是在解決空間機器人運動過程中的動量守恒問題、空間機器人本體和機械臂運動的耦合問題以及空間機器人的非完整約束問題。

對柔性臂空間機器人的研究多數是從動力學的角度出發[8-10]，解決柔性臂的跟蹤控制及振動抑制問題，很少從運動學角度研究柔性臂空間機器人，也鮮有從運動學角度出發對柔性臂空間機器人進行軌跡規劃，主要原因是柔性臂空間機器人的運動學建模以及軌跡規劃既要解決剛性臂空間機器人具有的上面3 個問題，還要解決機械臂連桿的彈性變形問題。空間機器人的柔性機械臂是一個無窮維的分布參數系統，考慮臂桿柔性的系統運動學方程非常復雜，很難將描述臂桿彈性變形的振動模態變量與機械臂關節的剛性轉角變量解耦。因此，建立柔性臂空間機器人的運動學模型必須用新的方法來描述柔性連桿彈性變形的運動變量。

文獻[11]中，T.Shimizu 等人提出了一種描述柔性機械臂連桿彈性變形的方法，他們利用柔性機械臂連桿末端的彎曲變形量以及變形角度作為運動變量，很好地描述了地面固定基座柔性機械臂的運動。本論文利用T.Shimizu 描述柔性連桿彈性變形的方法，建立大型柔性臂空間機器人的運動學模型，并為空間機器人的作業進行軌跡規劃。

1 柔性臂空間機器人的結構

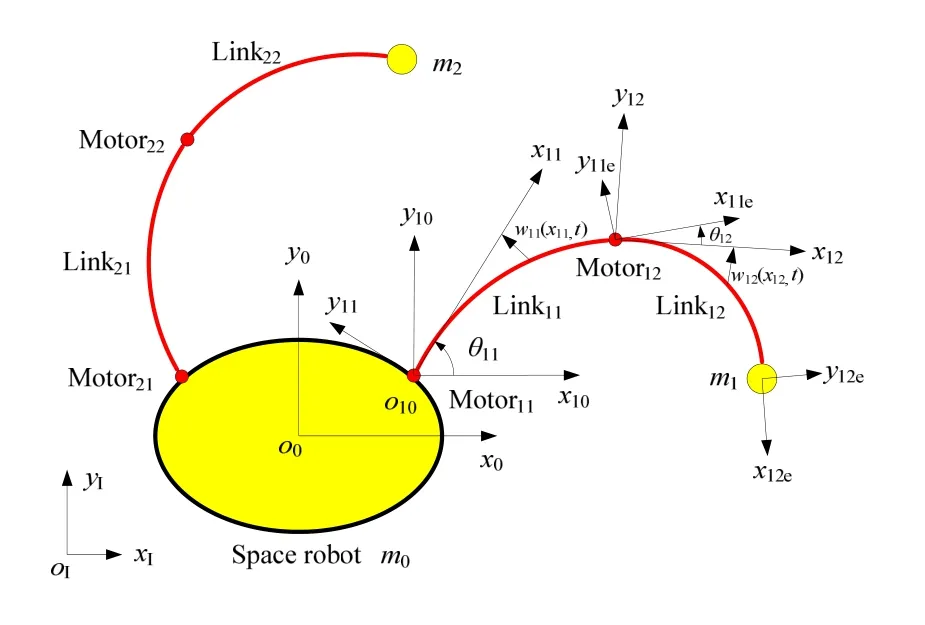
圖1 柔性臂空間機械人結構模型

柔性臂空間機器人為搭載了具有柔性特征機械臂的航天器，圖1 為具有一般性意義的結構模型。該空間機器人包括1 個剛性航天器本體，2 個柔性機械臂，每個柔性機械臂包括2 個柔性連桿和2 個旋轉關節，機械臂的末端各有一個具有集中質量的負載。

為方便討論，本文所用到的坐標系及符號定義如下：

∑I為慣性坐標系；∑0為空間機器人本體坐標系；∑i0為本體坐標系∑0平移到第i個機械臂的第1個旋轉關節處的坐標系；∑ij( 1≤i≤ 2，1≤j≤ 2)為第i個機械臂的第j個連桿的固連坐標系；∑ije為第i個機械臂的第j個連桿的末端坐標系；為空間機器人本體質心在慣性坐標系∑I內的位置；θ0(t)為空間機器人本體質心在慣性坐標系∑I內的姿態角；wij(xij,t)為柔性連桿Linkij在坐標xij和時間t時的橫向應變；w'11e為連桿Link11末端的切向量在坐標系∑11中的轉角；w'21e為連桿Link21末端的切向量在坐標系∑21中的轉角；θij(t)為機械臂關節電機Motorij在時間t時的剛性轉角。

柔性連桿上任一點的彈性變形wij(x,t)是無窮多個僅與x有關的振型模態函數Wk(x)和僅與t有關的簡諧振動函數δk(t)乘積的疊加。在實際應用中，一般取有限項的和，保留適當的振型模態，可以得到較高的精度，所以wij(x,t)可寫為

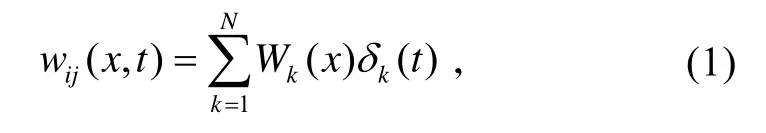
式中，N為所取的振型模態數。

2 柔性臂空間機器人的運動學方程

2.1 位置運動學方程

式中，R表示坐標變換矩陣。

機械臂2 的末端在慣性坐標系內的位置為

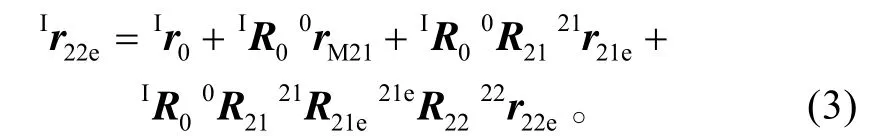
構造一個向量Ire，其包含機械臂1 和機械臂2的末端位置方程，則可得出柔性臂空間機器人的末端位置運動學方程：

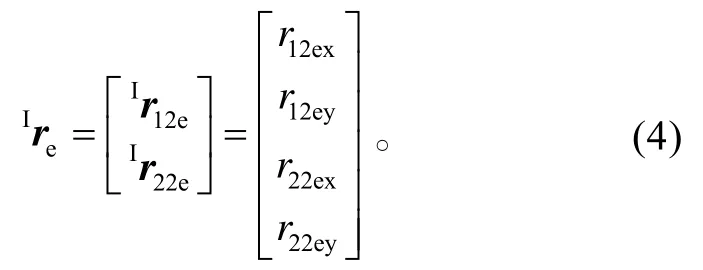
它表示機械臂柔性變形的廣義坐標。則，

式(5)表明，柔性臂空間機器人機械臂末端位置既是空間機器人本體位置和姿態的函數，又是機械臂剛性轉角和柔性變形的函數，對其求導，得

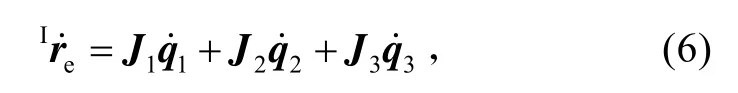
式中，

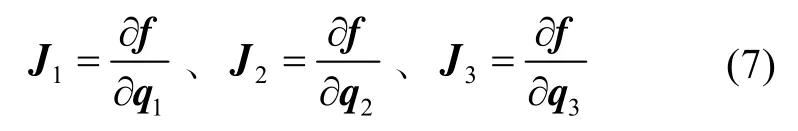
是函數f的雅可比矩陣。

2.2 柔性臂空間機器人動量守恒

不考慮軌道動力學情況下，自由漂浮空間機器人所受的合外力為0。因此，空間機器人的線動量及角動量(動量矩)保持守恒。

1)線動量守恒。空間機器人總的線動量是空間機器人本體動量、連桿 Link11的動量、連桿Link12的動量、機械臂1 末端負載的動量、連桿Link21的動量、連桿Link22的動量以及機械臂2 末端負載的動量的和。假設空間機器人系統在初始時刻的線動量為0，系統的動量守恒方程可表示為

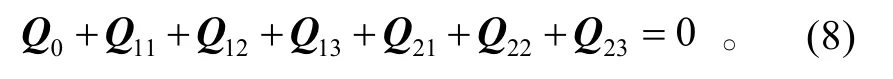
2)動量矩守恒。假設空間機器人系統在初始時刻的動量矩為0，系統的動量矩守恒方程可表示為

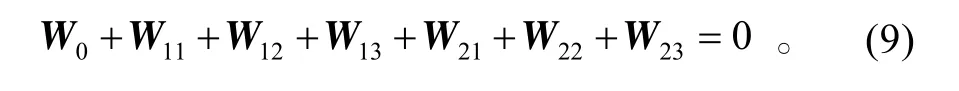
2.3 基于廣義雅可比矩陣的微分運動學方程

聯合式(8)和(9)，可得：

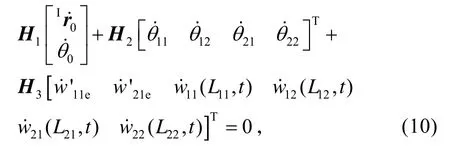
即，

H1是空間機器人的質量慣量矩陣，可逆。變換式(11)為

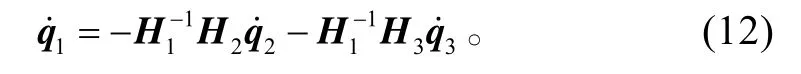
式(12)顯示了自由漂浮狀態下柔性臂空間機器人本體位姿與機械臂剛性轉角和柔性變形量之間的運動速率關系。把式(12)代入式(6)，可得柔性臂空間機器人基于廣義雅可比矩陣的微分運動學方程：

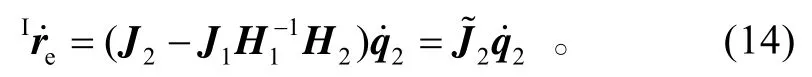
至此表明，式(13)表示了更具有一般性意義的空間機器人運動學模型，它包含了臂桿柔性因素對空間機器人末端位置運動的影響，剛性臂空間機器人運動學方程只是它的一個特殊形式。

3 柔性臂空間機器人軌跡規劃

如果空間機器人在完成任務的過程中，要求機械臂的末端嚴格按照直角坐標空間內期望的軌跡運動，則對這類任務的運動規劃就是直角坐標連續軌跡規劃。

自由漂浮模式下的空間機器人連續軌跡規劃，就是規劃機械臂關節角的運動，控制機械臂末端跟蹤期望的軌跡。

假設期望空間機器人末端按如下軌跡變化：

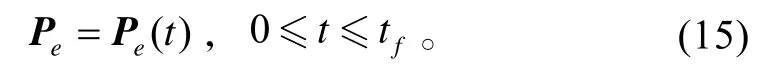
假設末端軌跡連續可微，可以對末端軌跡進行微分(對于分段可微函數，可以采用適當的過渡軌跡)，即：

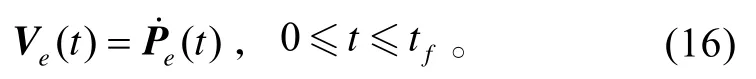
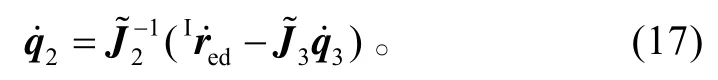
則期望的關節角為

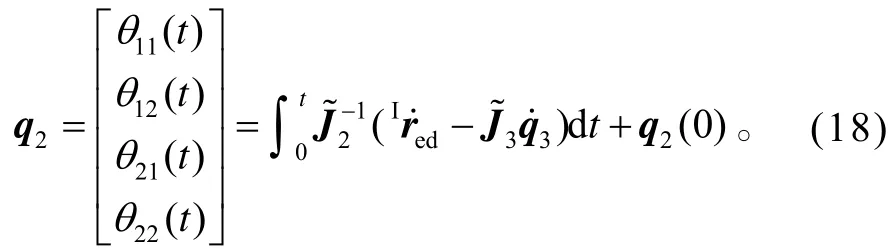
柔性臂空間機器人的連續軌跡規劃中，考慮了柔性臂的彈性振動對機械臂末端位置的影響，這將使規劃的機械臂關節運動能夠補償柔性臂彈性振動對機械臂末端位置的影響。但是，基于速度級運動學的軌跡規劃方法，有時會受雅可比矩陣奇異的影響。雅可比矩陣的奇異性不僅依賴系統的運動學參數，還依賴于動力學參數，即與系統質量和轉動慣量有關，所以稱空間機器人機械臂的運動奇異為動力學奇異[12]。在軌跡規劃及運動控制中，避免雅可比矩陣奇異的方法有奇異值分解法、阻尼最小方差法等[13-14]。

4 軌跡規劃仿真分析

4.1 仿真方法與流程

空間機器人機械臂末端軌跡的表示方法有多項式法、B 樣條函數法、神經網絡等多種方法，本文采用5 次多項式的方法來表示：

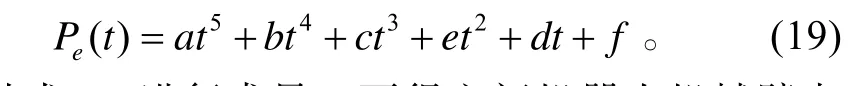
對式(19)進行求導，可得空間機器人機械臂末端運動速率。在規劃了機械臂末端運動軌跡及運動速率的條件下，對第1 節敘述的柔性臂空間機器人進行連續軌跡規劃仿真。

仿真程序使用MATLAB functions 文件編寫，程序流程是由時間驅動，時間步長為1×10?3s，也就是柔性臂桿振動的采樣頻率為1×103Hz。仿真中使用3 階振動模態來近似柔性臂的彈性振動，計算得柔性臂的第3 階振動模態固有頻率為17.7 Hz，振動采樣頻率滿足香農采樣定理。

在滿足計算精度要求的情況下，程序中的積分運算都采用歐拉法，這樣既簡化了程序，又加快了仿真運算速度。采用阻尼最小方差法來解決雅可比矩陣奇異時的規劃。仿真程序流程如圖 2 所示。

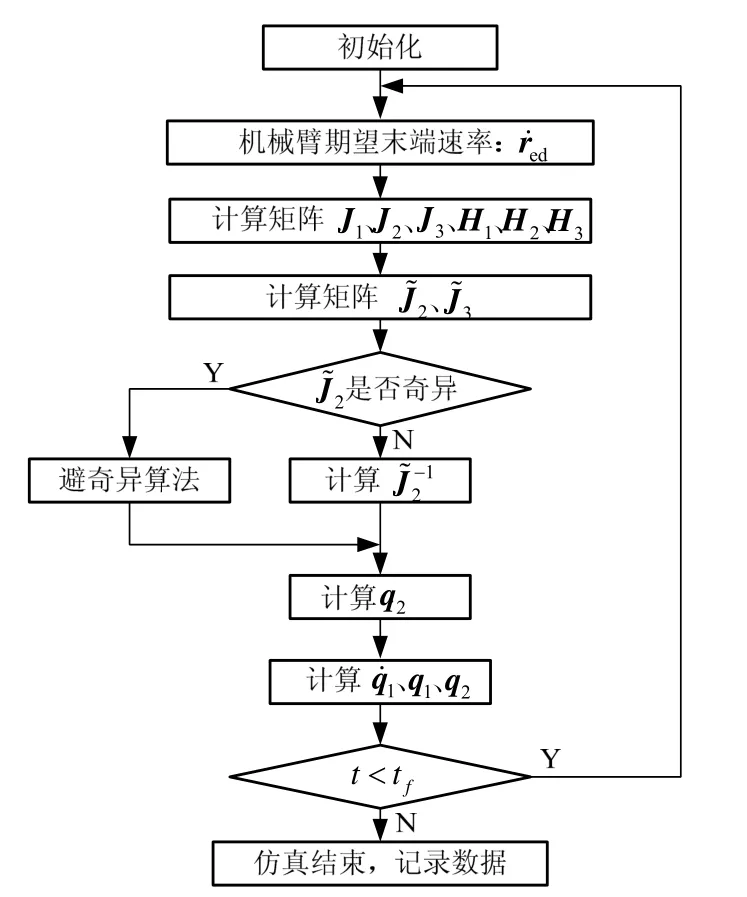
圖2 仿真程序流程圖

4.2 仿真結果分析

仿真中，柔性雙臂空間機器人結構參數設定如下：

空間機器人本體質量m0= 1 ×104kg，本體繞質心慣量I0= 1 ×105kg ?m2。

4 個機械臂連桿的幾何質量參數相同。臂桿長度L= 8m，質量密度ρA=50kg/m，抗彎剛度EI= 1 × 1 06N ?m2，振動模態及頻率可以通過計算得出。

仿真計算得出了空間機器人2 個機械臂的4 個關節轉角位置，如圖3 所示。從圖中觀察，規劃的機械臂關節轉角連續、光滑。機械臂若按照圖3 所示的關節位置運動，機械臂末端準確沿著規劃的軌跡運動，機械臂末端位置并沒有因為臂桿的彈性振動而發生振動，如圖4、圖5 所示。對規劃的機械臂關節轉角做離散傅里葉變換，得出機械臂關節轉角的幅頻特性曲線，如圖6 所示。通過關節轉角的幅頻特性曲線，發現規劃的關節轉角運動有振動現象，且振動頻率是機械臂柔性連桿的固有頻率，由此表明，機械臂連續軌跡規劃通過關節轉角的振動運動補償了柔性連桿的固有振動對機械臂末端位置的振動影響，使機械臂的末端嚴格按照規劃的軌跡運動，也實現了抑制機械臂末端位置振動的效果。

圖3 2 個機械臂的關節轉角

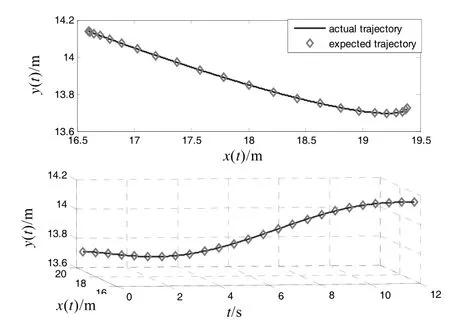
圖4 1 號機械臂末端位置

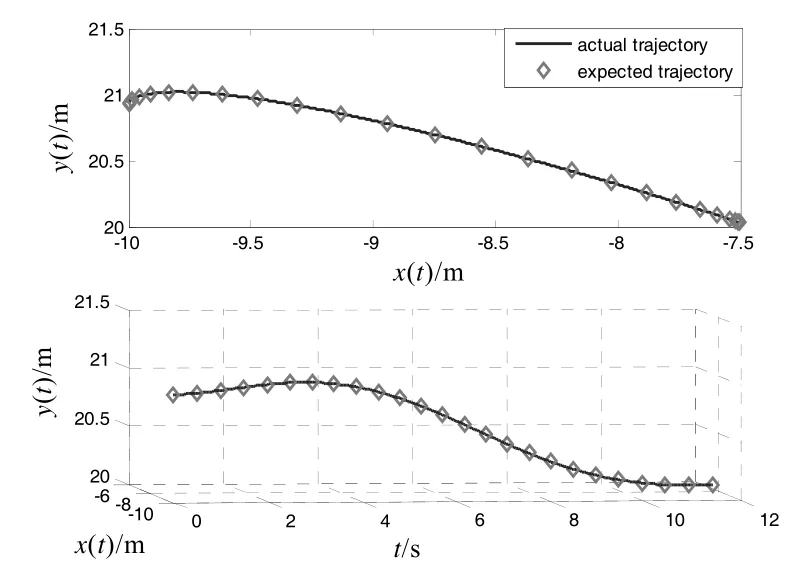
圖5 2 號機械臂末端位置

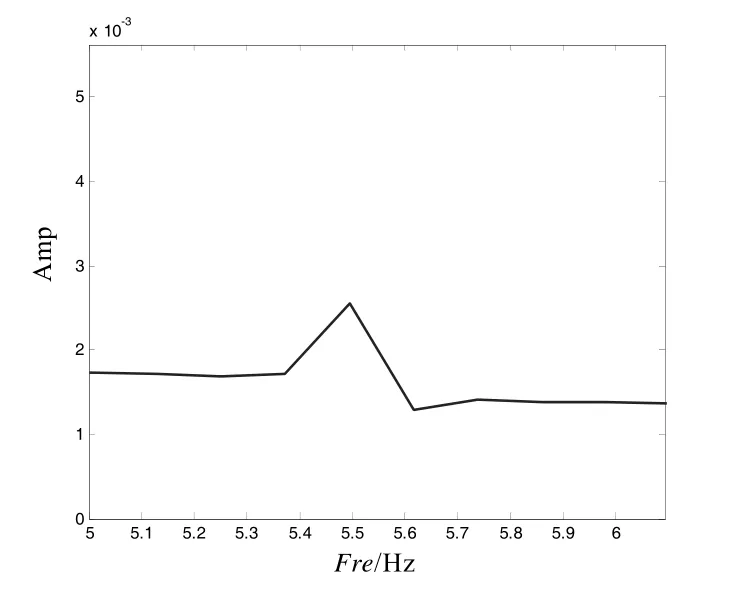
圖6 關節轉角的幅頻特性

由于在規劃過程中，沒有對空間機器人本體姿態及質心位置做限制，空間機器人本體姿態及質心位置在規劃的關節轉角運動的作用下發生運動，其運動如圖7、8 所示。

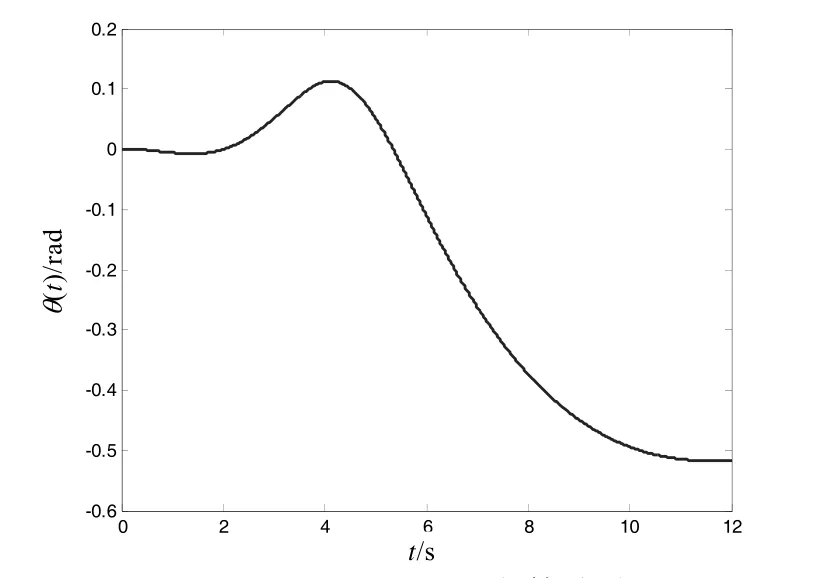
圖7 空間機器人本體姿態

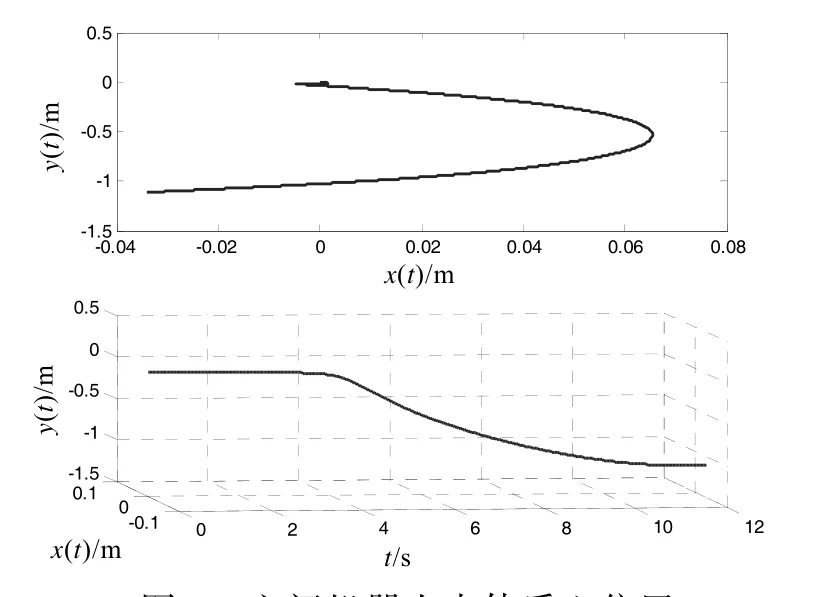
圖8 空間機器人本體質心位置

5 結論

空間機器人機械臂末端的精確定位既受到機械臂關節轉角的影響，又受到空間機器人本體位姿及機械臂柔性因素的影響，而這3 個因素又是相互耦合的。基于運動學模型的柔性臂空間機器人軌跡規劃可以綜合3 個因素對柔性臂末端位置的影響，特別是考慮了機械臂桿彈性振動對機械臂末端位置的影響，使柔性臂的末端準確沿著期望的軌跡運動。本文的仿真表明，規劃的關節轉角振動運動補償了柔性連桿的固有振動對機械臂末端位置的振動影響，使機械臂的末端嚴格按照期望的軌跡運動。

本文建立的柔性臂空間機器人“雙廣義雅可比矩陣”形式的運動學模型比單純的剛性臂空間機器人廣義雅可比矩陣更具有一般性意義，它不僅適用于柔性臂空間機器人，而且也適用于剛性臂空間機器人、剛性臂和柔性臂結合的空間機器人。以柔性臂空間機器人運動學模型為基礎，可以對柔性臂空間進行振動分析、軌跡規劃等研究，柔性臂空間機器人運動學模型的建立，為從運動學角度研究柔性臂空間機器人提供了理論基礎。

[1] VAFA Z, DUBOWSKY S. On the dynamics of manipulators in space using the virtual manipulator approach[C]//Proceedings 1987 IEEE International Conference on Robotics and Automation. Raleigh, NC, USA, 1987∶579-585.

[2] UMETANI Y, YOSHIDA K. Resolved motion rate control of space manipulators with generalized jacobian matrix[J]. IEEE Transactions on Robotics and Automation, 1989,5(3)∶303-314.

[3] YAMADA K, TSUCHIYA K. Efficient computation algorithms for manipulator control of a space robot[J]. Transactions of the Society of Instrument and Control Engineers, 1990,26(7)∶765-772.

[4] MUKHERJEE R, NAKAMURA Y. Formulation and efficient computation of inverse dynamics of space robots[J]. IEEE Transactions on Robotics and Automation, 1992,8(3)∶400-406.

[5] YOKOKOHJI Y, TOYOSHIMA T, YOSHIKAWA T. Efficient computational algorithms for trajectory control of free-flying space robots with multiple arms[J]. IEEE Transactions on Robotics and Automation, 1993,9(5)∶571-580.

[6] SUZUKI T, NAKAMURA Y. Planning spiral motion of nonholonomic space robots[C]//Proceedings of the 1996 IEEE International Conference on Robotics and Automation. Minneapolis∶ USA, 1996∶718-725.

[7] NAKAMURA Y, MUKHERJEE R. Exploiting nonholonomic redundancy of free-flying space robots[J]. IEEE Transactions on Robotics and Automation, 1993,9(4)∶499-506.

[8] 洪在地, 贠超, 陳力. 柔性臂漂浮基空間機器人建模與軌跡跟蹤控制[J]. 機器人, 2007,29(1)∶92-96.

[9] 王從慶, 張承龍. 自由浮動柔性雙臂空間機器人系統動力學建模與抑振控制[J]. 機械科學與技術, 2007, 26(2)∶192-196.

[10] 洪昭斌, 陳力. 柔性空間機械臂基于奇異攝動法的魯棒跟蹤控制和柔性振動主動控制[J]. 工程力學, 2010,27(8)∶191-197.

[11] SHIMIZU T, SASAKI M, OKADA T. Tip position control of a two links flexible manipulator based on the dynamic extension technique[C]//SICE Annual Conference 2007. Japan∶ Kagawa University, 2007∶ 868-873.

[12] PAPADOPOULOS E, DUBOWSKY S. Dynamic singularities in free-floating space manipulators[J]. Journal of Dynamic Systems, Measurement, and Control, 1993,115∶44-52.

[13] 顧曉勤, 劉延柱. 空間機械臂動力學奇點與回避[J]. 宇航學報, 1998,19(4)∶32-36.

[14] 吳劍威, 史士財, 劉宏. 自由飄浮空間機器人笛卡爾避奇異運動規劃[J]. 華中科技大學學報, 2009,37 (11)∶5-8.