旋轉捷聯慣導系統原理及典型方案分析

徐勝紅，金 斌，施建洪，李瑞濤

（1．海軍航空工程學院控制工程系，山東 煙臺 264001；2．海軍裝備部，北京 100036）

慣導系統具有工作自主性強、提供導航信息較為全面、抗干擾能力強、適用條件寬等獨特優點，但也存在定位誤差隨時間累積的缺陷。工程實踐中，一般通過誤差補償或研制更高精度慣性器件等技術途徑可以較好地提高慣導系統精度[1-2]。采用系統誤差補償技術與研制高精度慣性元件相比具有成本低、見效快的特點，其中，旋轉調制技術便是一項重要的系統誤差自動補償技術。旋轉調制誤差補償的技術特點是：將慣性元件漂移誤差調制成某種周期變化的形式，通過導航解算的積分運算過程自動將誤差平均抵消掉。

在光學陀螺捷聯慣導中，機械編排由計算機軟件實現，光學陀螺又具有動態范圍寬、標度因數線性度好、無機電干擾誤差項等特點。因此，光學陀螺捷聯慣導非常適合采取旋轉調制技術實現誤差補償[3]。

國外基于旋轉調制方法的捷聯慣導誤差自動補償技術在艦船導航領域已經得到應用，如美國早在上世紀就先后研制出了MK39、MK49 系列等高精度旋轉捷聯慣導系統并應用[4]。國內眾多科研機構和學者對這項技術也進行了大量的研究[5]，但受光學陀螺發展相對滯后、精度較低的限制，該技術的應用仍不成熟。

1 旋轉捷聯慣導誤差補償原理

在捷聯式慣導系統中，旋轉自動補償技術在本質上是在轉動周期內周期性地改變姿態矩陣，使得系統中緩慢變化的誤差在轉動周期內均值接近零，從而減小系統誤差的積累，提高導航精度[6]。旋轉方法還可以提高系統對準時的可觀測度，提高對準的精確度[7]。

光學陀螺捷聯慣導系統用建立的“數學平臺”作為導航計算的參考坐標系，系統的誤差傳播方程可以用下列式子表示[1，8]：

姿態誤差為

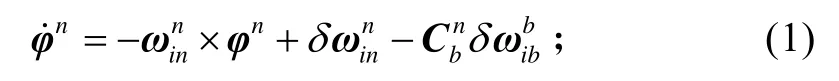
速度誤差為

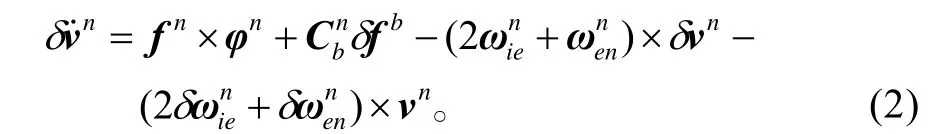
式(1)、(2)中：i表示慣性坐標系；e表示地球坐標系；n表示導航坐標系；b表示載體坐標系；nφ是計算坐標系與理想導航坐標系之間的失準角，也就是慣導姿態誤差角；ω和δω分別是角速率和角速率誤差，其上標表示在對應坐標系內的分量值，下標表示相對運動的坐標系；v和δv分別是速度和速度誤差；f和δ f分別是比力和比力誤差；是姿態矩陣。數據，供導航解算使用。

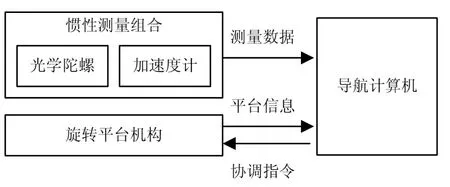
圖1 旋轉捷聯慣導系統結構原理示意圖

選擇東北天地理坐標系為導航坐標系n，初始狀態載體坐標系b與導航坐標系n重合。令旋轉平臺坐標系為r，忽略陀螺儀和加速度計安裝和刻度系數誤差，同時令陀螺漂移為ε，加速度計零偏為?。當平臺繞臺體z軸作單軸旋轉時，有其中，是平臺相對載體旋轉的角速率值。

假設是準確的，則

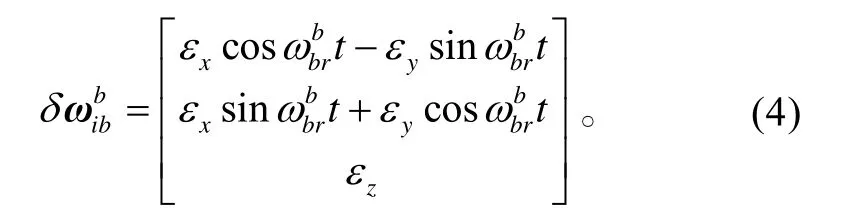
同樣，可以得到：

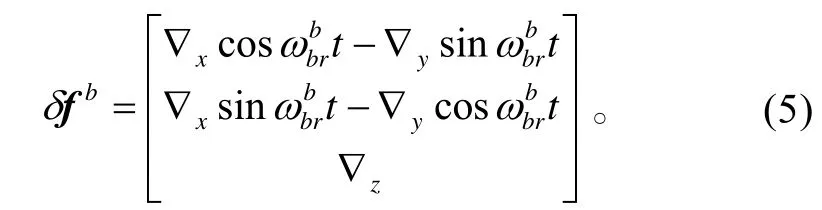
如果ε和?為常值，則和δfb的水平分量將按正弦規律以周期2π/ω變化，使其在一個轉動周期內均值為零。因此，理論上旋轉能夠抵消敏感軸與轉軸方向垂直的陀螺儀和加速度計常值誤差。

2 捷聯慣導典型旋轉方案分析

旋轉捷聯慣導系統實現誤差補償的關鍵是IMU 需要周期性地旋轉，因而首先需要解決旋轉方案問題。理論上，旋轉捷聯慣導可以有單軸、雙軸、三軸等不同方案[10]，不同旋轉方案的作用和效果也不同。當前針對單軸和雙軸方案的研究較多，而單軸方案又有連續旋轉和正反轉停兩種具體形式。

2.1 單軸連續旋轉方案

單軸連續旋轉方案是最為簡單的一種旋轉調制誤差補償方案，即IMU 借助平臺機構繞某個軸作連續的常值速率旋轉，旋轉軸通常是臺體的z軸。

在連續旋轉方案中，為常值。考慮靜止導航狀態且假定載體坐標系與導航坐標系重合，則：fn=[00?g]T，vn=[000]T，=I3。

于是式(1)、(2)分別簡化為：

當IMU 不旋轉時，即通常的捷聯慣導系統經緯度誤差、東向和天向姿態誤差及東向速度誤差曲線如圖2 所示。當IMU 繞臺體z軸連續旋轉時，結合式(4)、式(5)，令=1.5(°)/s，可得到捷聯慣導經緯度誤差、東向和天向姿態誤差及東向速度誤差曲線如圖3 所示。

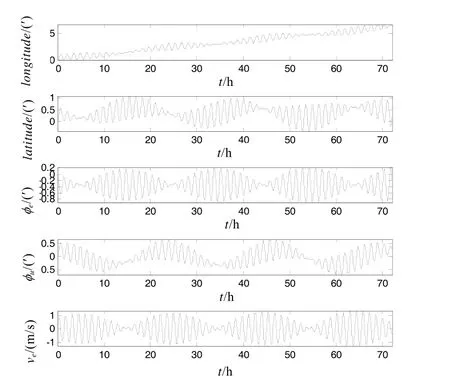
圖2 IMU 不旋轉時捷聯慣導誤差曲線圖

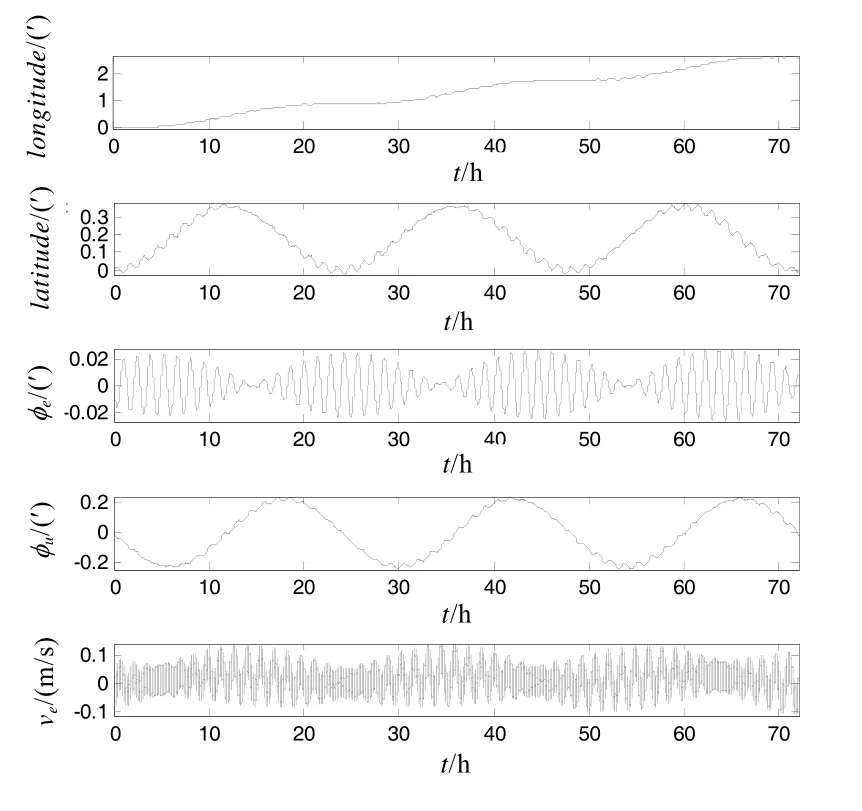
圖3 IMU 單軸連續旋轉時捷聯慣導誤差曲線圖

可以看出，當IMU 繞臺體z軸旋轉時，與轉軸方向垂直的誤差分量得以大大降低，慣導系統輸出精度有較大提高，水平姿態精度的提高尤為明顯。

2.2 單軸正反轉方案

正反轉停方案是當前研究較多的單軸旋轉方案。一種典型的設計是4 個位置的正反轉/停[10]，轉動方式如圖4 所示：先繞zb軸正轉(逆時針)180°，停止一段時間后再反轉(順時針)180°并停止一段時間；接著繞zb軸反轉180°并停止一段時間，再正轉180°后停止一段時間。以上轉動次序為一個周期，之后循環。

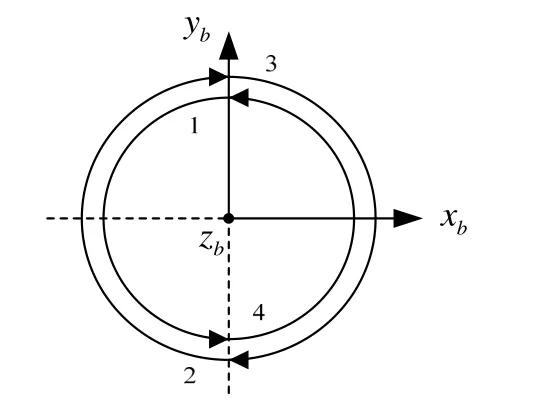
圖4 單軸正反轉停旋轉方案示意圖

假定 IMU 繞臺體z軸正反轉的角速率，停止時間30 s，即IMU 正反轉停一個完整周期為600 s，可以得到系統經緯度誤差、東向姿態誤差和東向速度誤差曲線如圖5 所示。

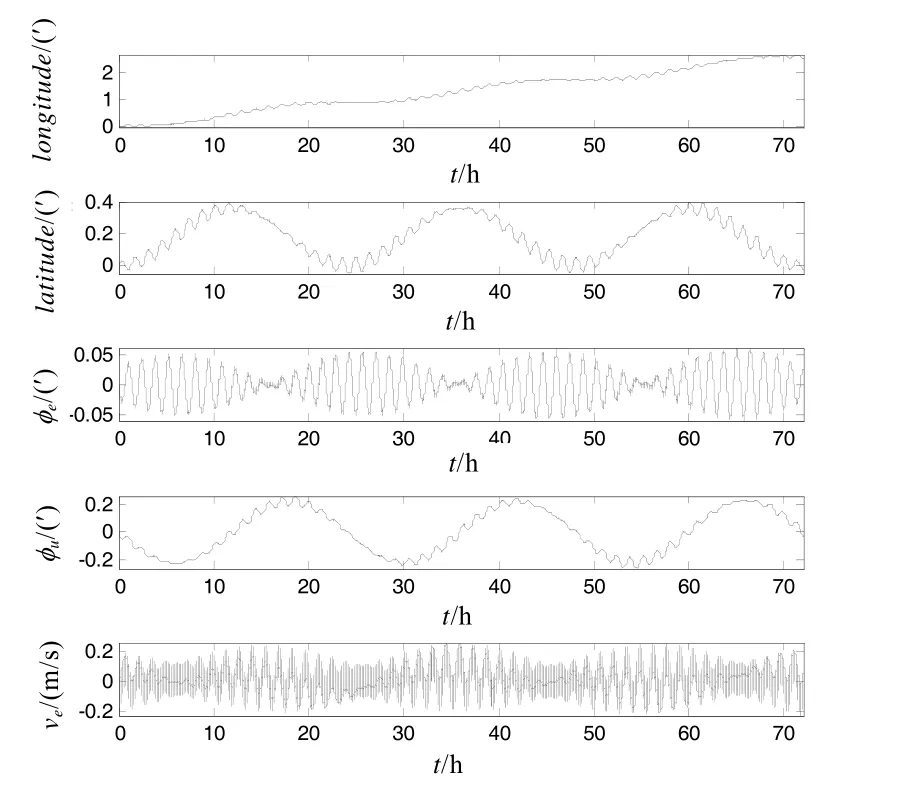
圖5 IMU 單軸正反轉停方案的捷聯慣導誤差曲線圖

比較圖5 和圖2 可以看出，當IMU 繞臺體z軸作周期性的正反轉停旋轉時，與轉軸方向垂直的誤差分量也能夠大大降低。將圖5 的結果與圖3 相比較會發現，正反轉停方案的系統精度比連續旋轉方案有所降低。不過，更多的研究表明，正反轉停方案有利于提高系統可靠性[10-12]和環境適應能力，綜合性能更優，這也是當前多采用這種方案的原因。

2.3 雙軸旋轉方案

雙軸旋轉方案通常選擇臺體的z軸及某個水平軸(比如x軸)作為旋轉軸。一種較為典型的雙軸旋轉方案是[2，11]：先繞臺體z軸正轉180°，停止一段時間后繞臺體x軸正轉180°并再停止一段時間；接著繞z軸反轉180°并停止一段時間，再繞x軸反轉180°，停止一段時間；然后按以上次序反向轉動一次。以上旋轉執行完畢為一個周期，即每個完整周期包括8 個階段，之后循環。

假定IMU 繞臺體z軸及x軸正反轉角速率值均相同并以表示，則8 個階段的旋轉過程中可分別表示如下。

第2 階段：

類似地，第3 階段：

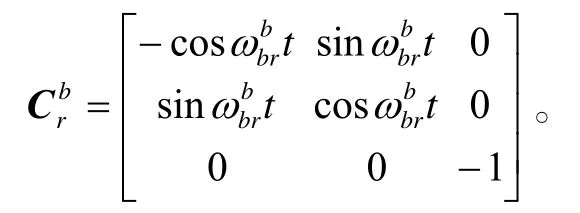
第4 階段：

第5 階段：

第6 階段：

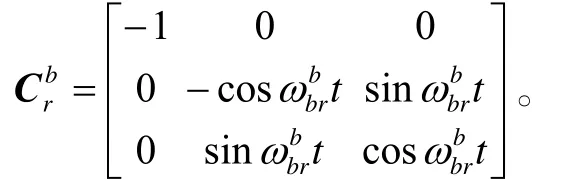
第7 階段：

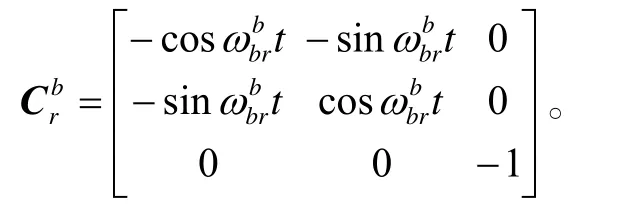
第8 階段：

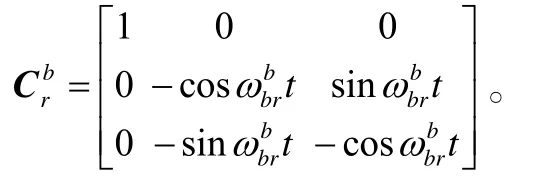
從以上8 個階段的分析可以看出：IMU 在3 個軸的慣性元件輸出誤差在雙軸旋轉狀態下均被調制，因此雙軸旋轉方式的補償方法等效于兩個單軸交替旋轉。假定雙軸旋轉的角速率停止時間30 s，即一個完整周期為1 200 s，則可以仿真得到系統經緯度誤差、東向姿態誤差、天向姿態誤差、東向和北向速度誤差曲線如圖6 所示。

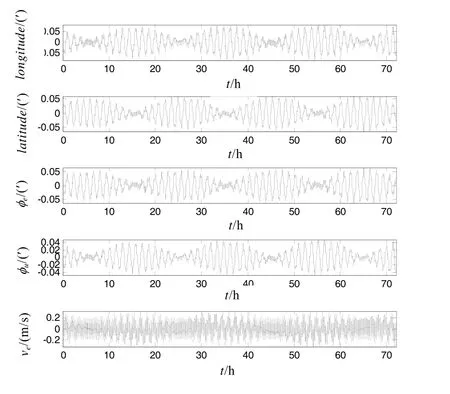
圖6 IMU 雙軸旋轉方案的捷聯慣導誤差曲線圖

比較圖6、圖5 和圖2 可以看出，在雙軸旋轉方案中，IMU 的陀螺儀和加速度計在3 個軸方向上的誤差都能夠得到補償，其水平速度和姿態補償效果與單軸正反轉停方案相當，但位置精度更高，而天向姿態精度可以有較大改善。

3 結束語

國內外眾多的研究表明，以光學陀螺IMU 為核心的旋轉捷聯慣導系統具備獨特的技術優點，發展和應用前景良好。這里通過對幾種典型IMU 旋轉方案的分析和仿真，表明單軸旋轉能夠補償與轉軸相垂直方向上的陀螺儀和加速度計常值誤差，而雙軸旋轉能夠補償全部3 個軸上的陀螺儀和加速度計常值誤差。由于捷聯慣導系統中引起誤差的因素非常多[13]，旋轉捷聯慣導系統的誤差傳播過程必然是非常復雜的。因此，盡管有國內外不少學者在此領域進行了不少理論的甚至工程化的研究，針對旋轉捷聯慣導系統仍值得作更深入的研究。

[1] 張樹俠, 孫靜. 捷聯式慣性導航系統[M]. 北京∶ 國防工業出版社, 1992∶138-158.

[2] 田亞軍, 周剛, 胡軍照, 等. 捷聯慣導系統姿態算法實現及工程應用[J]. 四川兵工學報, 2011,32(1)∶11- 12.

[3] 袁保倫, 饒谷音. 光學陀螺旋轉慣導系統原理探討[J]. 國防科技大學學報, 2006,28(6)∶76-80.

[4] LAHHAM J I, BRAZELL J R. Acoustic noise reduction in the MK 49 ships inertial navigation system[C]//IEEE Position Location and Navigation Symposium. 1992∶ 32-39.

[5] 孫楓, 孫偉, 郭真. 基于IMU 旋轉的捷聯慣導系統自補償方法[J]. 儀器儀表學報, 2009,30(12)∶2511-2517.

[6] ISHIBASHI S, TSUKIOKA S, SAWA T. The rotation control system to improve the accuracy of an inertial navigation system installed in an autonomous underwater vehicle[C]//Workshop on Scientific Use of Submarine Cables and Related Technologies 2007. 2007∶495-498.

[7] ISHIBASHI S, TSUKIOKA S, YOSHIDA H. Accuracy improvement of an inertial navigation system brought about by the rotational motion[C]//OCEANS 2007- Europe. 2007∶1-5.

[8] 吳自飛, 朱海, 高大遠, 等. 單軸旋轉慣導系統建模與仿真[J]. 裝備制造技術, 2010,10∶5-8.

[9]李仁, 曾慶雙, 陳希軍. 基于光學陀螺慣導系統的誤差自動補償技術[J]. 電機與控制學報, 2010, 14(6)∶ 98-104.

[10] 李仁, 陳希軍, 曾慶雙. 旋轉式捷聯慣導系統誤差分析[J]. 哈爾濱工業大學學報, 2010,42(3)∶368-372.

[11] 楊益興, 田海濤, 周學文. 旋轉式捷聯慣導系統的誤差分析與仿真[J]. 艦船電子工程, 2010,30(5)∶86- 90.

[12] 翁海娜, 陸全聰, 黃昆, 等. 旋轉式光學陀螺捷聯慣導系統的旋轉方案設計[J]. 中國慣性技術學報, 2009, 17(1)∶8-14.

[13] 袁保倫, 饒谷音, 廖丹. 旋轉式慣導系統的標度因數誤差效應分析[J]. 中國慣性技術學報, 2010,18(2)∶ 160-164.