短波信道下基于PSWF的非正弦時域正交信號調制解調實現

孫小東，潘耀宗，2，康家方，李 丹

（1．海軍航空工程學院電子信息工程系，山東 煙臺 264001；2．92407 部隊，河北 秦皇島 066200； 3．中國聯合網絡通信有限公司煙臺市分公司，山東 煙臺 264000）

短波通信是歷史悠久、應用廣泛的通信方式之一。盡管當前許多新興的通信技術不斷吸引著人們的眼球，但是短波通信憑借著設備輕便、易于架設、使用維護簡單、通信距離遠、傳輸無須中介、頑存性強等優點，始終在國家戰略通信網中占有一席之地。隨著微電子、數字信號處理、自適應等現代信息技術的發展及其在短波通信中的應用，短波通信性能得到了極大改善。在通信技術發展的道路上，短波通信正在向以網絡化、數字化為主要技術特征的第三代短波通信邁進[1]。

短波通信雖優勢獨特，但受到可用頻帶窄、多徑時延、頻移等短波信道固有特性的影響[2]。基于橢圓球面波函數(Prelate Spherical Wave Function，PSWF)的非正弦時域正交調制技術，采用多路并行傳輸，延長了碼元的持續時間，增強了對短波信道多徑效應的抵抗能力。PSWF 的高能量聚集性，又可以極大地降低對其他頻段通信的干擾。并且，頻帶利用率較OFDM 技術可以更快的接近理論極限值[3]。所以，研究其在短波通信中的應用，對提高短波通信的性能有重要意義。

目前，在短波頻段內基于PSWF 的非正弦時域正交調制解調動態仿真實現、仿真中小相對帶寬PSWF 脈沖生成，為原理樣機的實現提供先驗支撐等方面，還未見文獻進行相關報道。本文利用Simulink 軟件對基于PSWF 非正弦時域正交信號的調制解調進行了實現，并在短波頻段內進行了性能仿真，對得到的仿真結果進行了分析。這對研究非正弦時域正交調制信號在短波信道內的特性和原理樣機的實現有重要意義。

1 短波信道仿真模型分析

1.1 短波信道仿真模型的主要類型

短波信道仿真模型主要有2 大類：基于統計的仿真模型和基于探測信號記錄的重放仿真模型。

1)基于統計的仿真模型可以進行若干固定條件(多徑、多普勒條件等)下的仿真。可以分為窄帶信道仿真模型和寬帶信道仿真模型。適用帶寬小于12 kHz 的模型稱為窄帶信道仿真模型，適用帶寬大于12 kHz 的模型則是寬帶信道仿真模型。Watterson模型是傳統窄帶信道模型中的標準模型，自1969年被Watterson 等人提出后，該模型得到廣泛接受，并被CCIR 推薦。寬帶信道模型中最具代表性的是上世紀90年代提出的ITS 模型。它主要是針對Waterrson 模型不能準確反映高緯度地區和近赤道地區電離層特性的局限性而提出的。盡管ITS 模型是作為寬帶模型被提出的，但它適用于窄帶和寬帶2 種情況。

2)基于探測信號記錄的重放仿真模型是利用具有代表性的探測記錄完成對短波信道仿真。信道仿真過程見圖1。第一步是通過發送短波頻段內的探測信號完成信號探測記錄，并記錄信道噪聲。(圖中虛線外的部分)；第二步是通過探測信號記錄，提取信道的沖激響應，經過濾波進一步減小其噪聲，最后和仿真信號進行卷積，并且疊加記錄的噪聲，得到經過短波仿真信道的信號(圖中虛線內的部分)[1]。進行仿真的時候要選用具有代表性的探測結果。

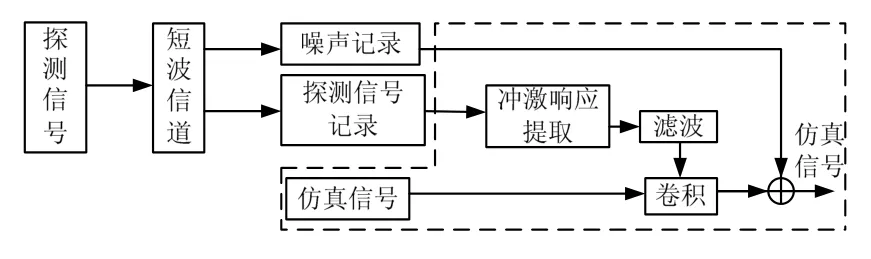
圖1 重放仿真模型

由于實驗條件的限制，本文采用的是基于統計的短波信道仿真模型。由于研究的對象是3 kHz 帶寬的短波信號，所以采用的是窄帶信道仿真模型。考慮到ITS 模型的復雜度較高，本文最終選用窄帶短波信道仿真模型中的代表：Watterson 短波信道仿真模型。

1.2 Watterson 短波信道模型原理

Watterson 模型將短波信道看作由帶抽頭的理想延遲線構成，每個抽頭系數對信號進行調制，從而使信號發生多普勒頻移、衰減等，最后各抽頭上的信號疊加，并混入高斯白噪聲。具體流程如圖2所示。

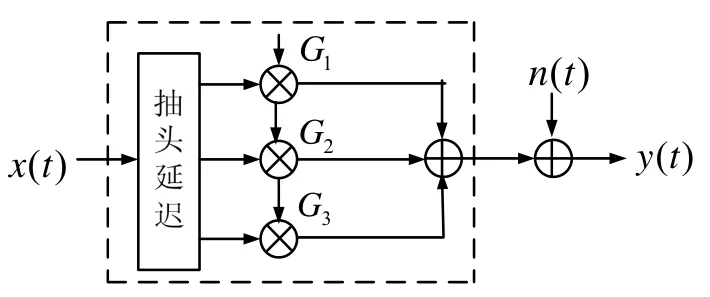
圖2 Watterson 短波信道模型原理圖

輸入信號x(t) 在各個路徑上經過不同的時延，在抽頭系數的作用下發生了多普勒頻移、衰減等各路疊加后被加入高斯白噪聲n(t) ，最后形成經過仿真信道的信號y(t) 。圖2 中虛線內的部分，可用信道沖擊響應h(t) 表示。

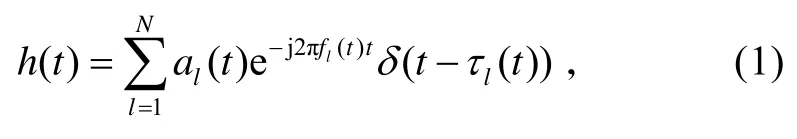
式中：N表示一共有N條傳輸路徑，τl(t)表示第l條路徑上t時刻的相對時延，al(t)表示第l條路徑上t時刻相對于主徑的幅值，fl(t)表示第l條路徑上t時刻的頻移。雖然，短波信道是時變的，但是在有限的時間和帶寬下，信道特性可以保持平穩[4]。為方便分析，假設頻移、相對時延和各路的相對幅值，都是靜態的。h(t) 被簡化為

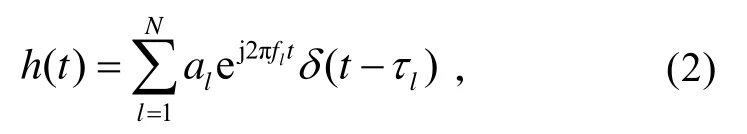
式中：N取值2～4 的約占85%[5]；lτ取值0.5～5 ms的約占99%[6]；lf取值大約在1～2 Hz[1]。此為仿真分析的取值范圍。

信號x(t) 經過短波信道模型后的y(t) 的表達式為

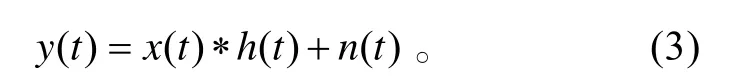
2 基于PSWF 的短波非正弦時域正交信號生成調制解調原理

2.1 短波頻段內PSWF 的生成

目前對PSWF 數值求解有很多算法，可歸納為3 種：第一是利用PSWF 的微分方程定義式，采用Legendre 多項式逼近，通過迭代得到近似解[7-8]。此方法以迭代的計算量換取求解的精度。盡管數值解精度高，但運算量大、效率低。第二是利用采樣定理建立PSWF 積分方程定義式與矩陣的對應關系，通過求矩陣的特征向量，求得PSWF 近似數值解[9-10]。此方法可以產生任意波段的橢圓球面波，但是在構建矩陣時，同樣存在著計算量大的問題。第三種是基于信號通過帶通濾波器的思想，由PSWF的頻域積分方程求得其時域積分表達式，離散化后構造Toeplitz 矩陣，最后通過計算其特征向量得到PSWF 的近似解[11]。此方法計算速度快、物理意義明確，但是僅能利用求解信號的離散采樣值。

在仿真過程中，考慮到前2 種方法求解效率低，本文采用了第3 種方法，但是，短波頻帶上產生3 kHz 帶寬的PSWF 時，遇到了小相對帶寬信號采樣率太高，致使仿真軟件中Toeplitz 矩陣不能正常運算的問題。故本文采用文獻[12]提出的一種PSWF的重構算法。

該算法的基本思想是：首先，依據采樣定理得到能夠準確恢復該PSWF 信號的最低采樣頻率；其次，構造并解得Toeplitz 矩陣的特征向量；最后，通過重構表達式得到預求的PSWF 數值解。該方法求解過程中不涉及迭代和積分運算，計算量小、求解效率高，不受采樣率限制，易于工程實現。盡管重構過程中，對PSWF 的能量集中度有一定影響，但程度很小，仍可滿足工程應用的要求。

求解具體步驟如下：

1)根據待求PSWF 的帶寬B0、脈沖持續時間t0、中心頻率f0和時間帶寬積C確定求解參數。由f0和B0確定B≥B0，使其滿足

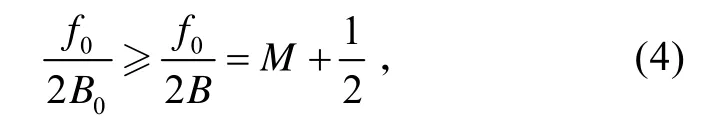
式中，M為正整數。

由帶通采樣定理確定采樣頻率fs≥fN=4B，再由sf及t0確定最低采樣點數：

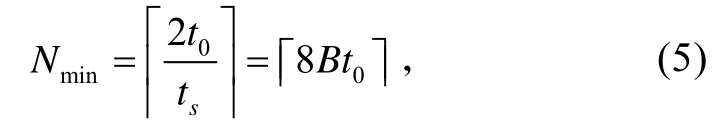
式中，┍┑表示向上取整。由f0和B求得重構函數k(t)的表達式：

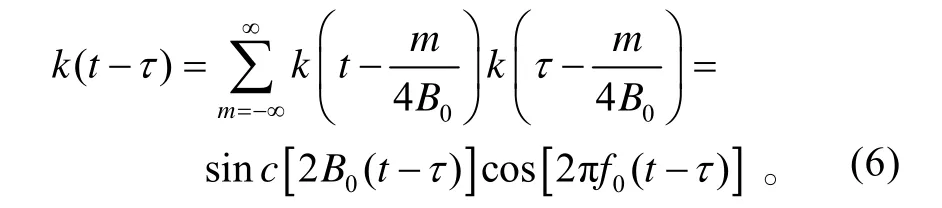
2)根據最低采樣點數Nmin，計算得到PSWF 的采樣值。即：

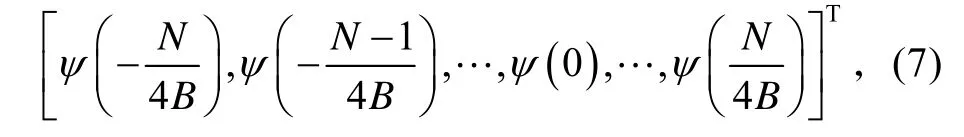
其中，連續的ψ中得到其不同時刻的離散值。

3)將k(t) 和所得PSWF 的采樣值代入式(8)便可以得到PSWF 的重構解。

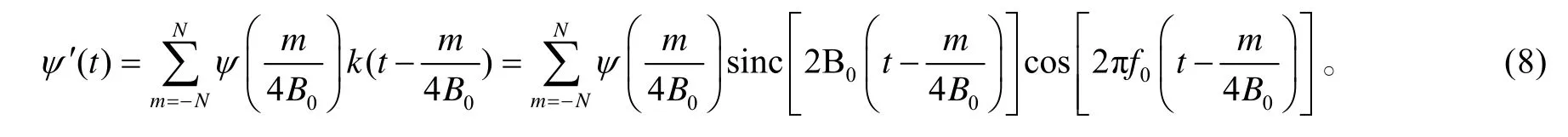
2.2 非正弦時域正交信號調制解調原理

非正弦時域正交信號調制解調的基本思想是，數據流經過串并變換后，各路分別選取PSWF 脈沖集中的一個脈沖進行調制，產生的各路調制信號相加，得到待發射的調制信號。經信道后，在解調端利用PSWF 脈沖的正交性，采用相關解調方式得到各路數據，經并串變換后得到數據流。基本流程如圖3 所示。

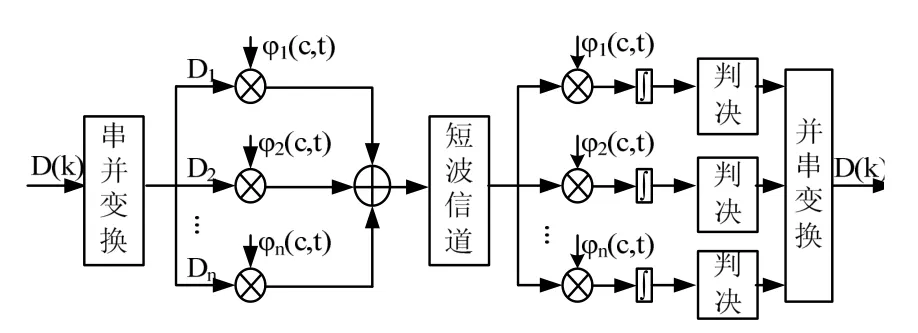
圖3 時域正交信號調制解調流程圖

數據流D(t) 串并變換后，分別與進行調制并合成一路經短波信道后，接收信號分別與?i(c,t)進行相關運算，通過判決得到每路的傳輸數據。最后，進行并串變換得到預傳輸的數據流D(t) 。

3 基于Simulink 的仿真模型建立

在利用Simulink 對短波信道條件下非正弦時域正交信號調制解調進行實現時，共分為：信源和PSWF 脈沖生成、時域正交調制、仿真短波信道、解調、誤碼率計算等模塊。

調制路數為4 時，仿真模型如圖4 所示。

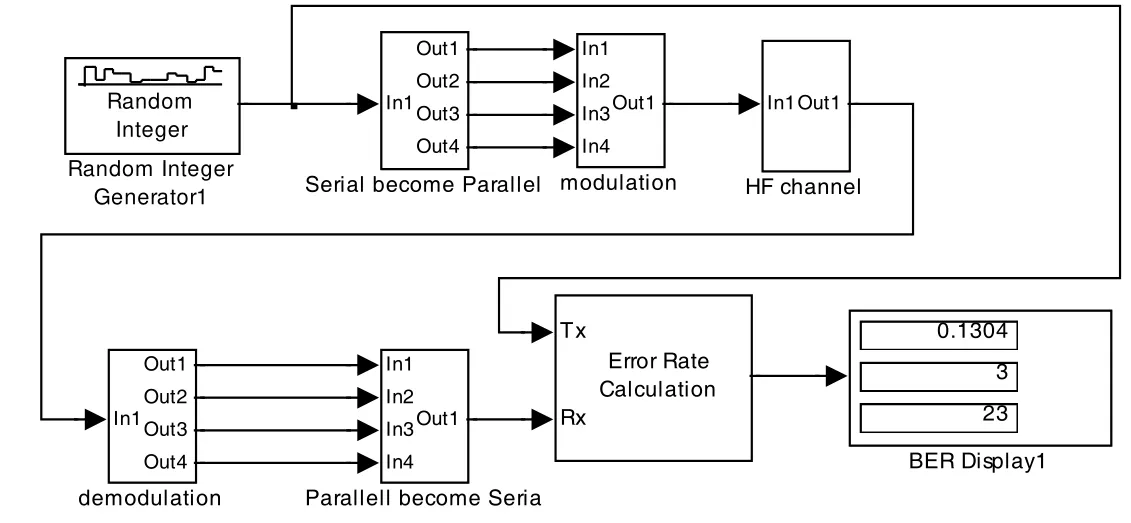
圖4 仿真系統模型

由隨機數生成模塊作為信源產生傳輸數據，串并變換模塊后傳輸數據由一路變為多路，在調制模塊用PSWF 脈沖進行調制后疊加，然后經過短波信道仿真模塊進行信道仿真，而后在解調模塊進行相關解調，經并串變換模塊得到接收數據，最后通過誤碼計算器來計算誤碼率。

1)信源和PSWF 脈沖生成。利用隨機數生成模塊，隨機等概生成1 和0，作為仿真模型的信源。本文采用2.1 節說明的方法進產生，短波頻段內的PSWF 脈沖。

2)串并變換模塊。模塊結構如圖5 所示。由0和1 組成的數據流從端口“In1”進入，經過“Swich”模塊后變為對應的由?1 和1 組成的數據流。經過“Buffer”和“MultiportSelector”后，最終數據流由 1路變為了4 路，此時的碼元持續時間為串行碼元持續時間的4 倍。

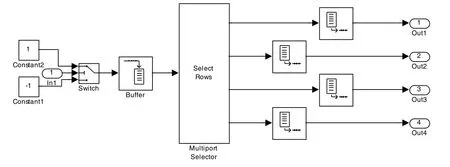
圖5 串并變換模塊

3)調制模塊。調制模塊的結構如圖6 所示。4路并行傳輸的數據分別經“In1”到“In4”進入調制模塊，通過相乘器對存儲在“direct sine table”模塊中的PSWF 脈沖，進行調制。其中第一路中“direct sine table”模塊存儲的是第一階PSWF 脈沖，以此類推，調制的路數決定了一共選擇脈沖的個數。各路信息調制到PSWF 脈沖上后，經過相加器得到合成的信號，從端口“out1”發出。圖7 從上至下依次是第1路調制信號、第3 路調制信號、合成后信號的時域波形。圖8 為合成信號的頻譜圖，主瓣從3 MHz 到3.003 MHz。

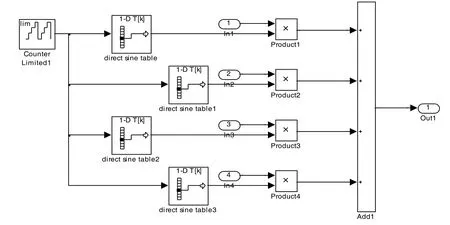
圖6 調制模塊

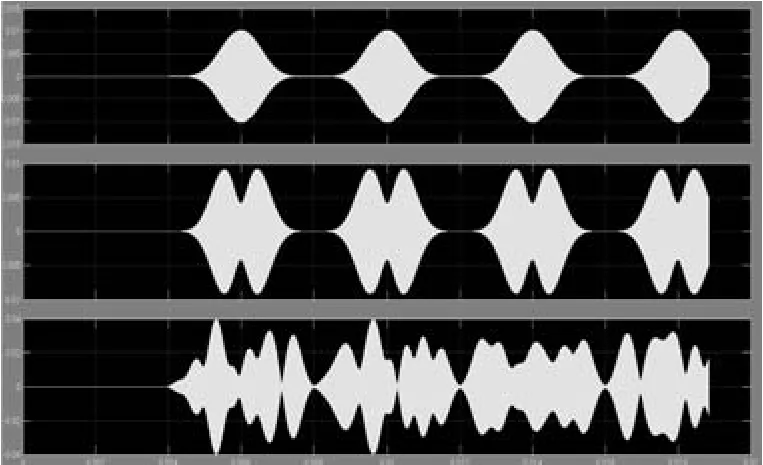
圖7 第1 路、第3 路和合路的調制波形

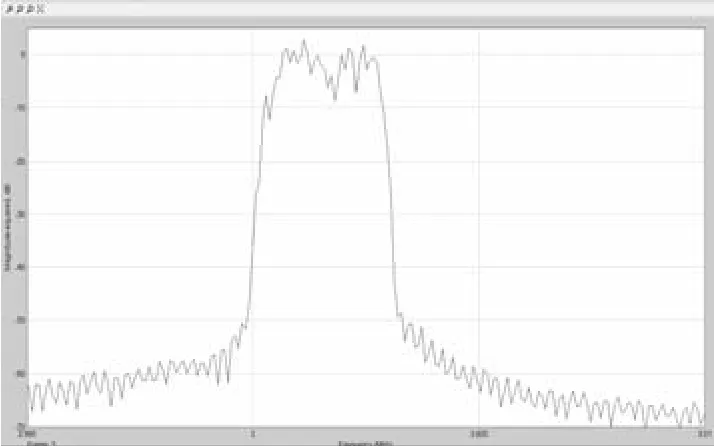
圖8 合成信號的頻譜圖

4)短波信道模塊。模塊結構如圖9 所示。調制模塊輸出的信號，從端口“In1”進入信道模塊。在信道模塊中首先經過“Analytic Signal”模塊，使其經過Hilbert 變換后，與原實信號合成復信號。然后將基于采樣的格式轉換為基于幀的格式，之后信號進入“Multipath Fading”模塊和“AWGN”模塊，這2 個模塊構成了對短波信道特性的仿真。最后信號格式反變換為基于采樣的格式，并取出其實部。圖10 為經過信道后的時域波形圖。

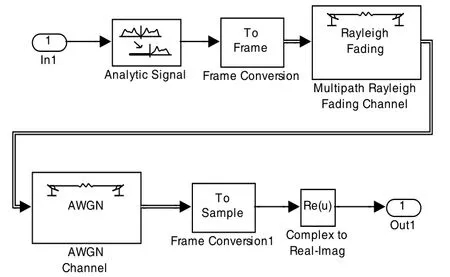
圖9 短波信道模型

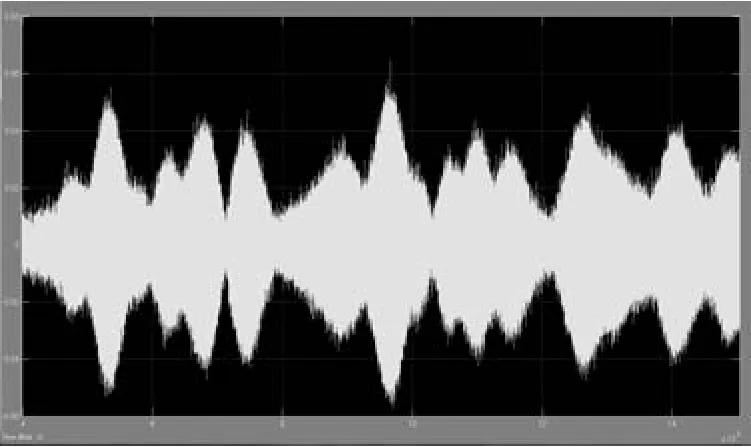
圖10 經過信道后的時域波形

5)解調模塊。模塊結構如圖11 所示。來自信道的信號通過端口“In1”進入到解調模塊。通過“Buffer”將一個碼元時間內的采樣值一起輸出，并且通過相乘器和存儲在“direct sine table”模塊中的PSWF 脈沖進行相關解調，得到各路數據，然后經過“Switch”模塊將由1 和?1 組成的數據，對應為由1 和0 組成的數據。最后經端口“Out1”到“Out4”輸出各路解調數據。

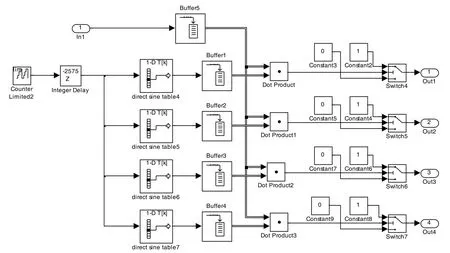
圖11 解調模塊

6)并串變換模塊。模塊結構如圖12 所示。從解調模塊輸出的4 路信號分別由端口“In1”到“In4”輸入，經過“Multiport Switch”模塊，使并行的數據變為串行的數據流，由“Out1”輸出。

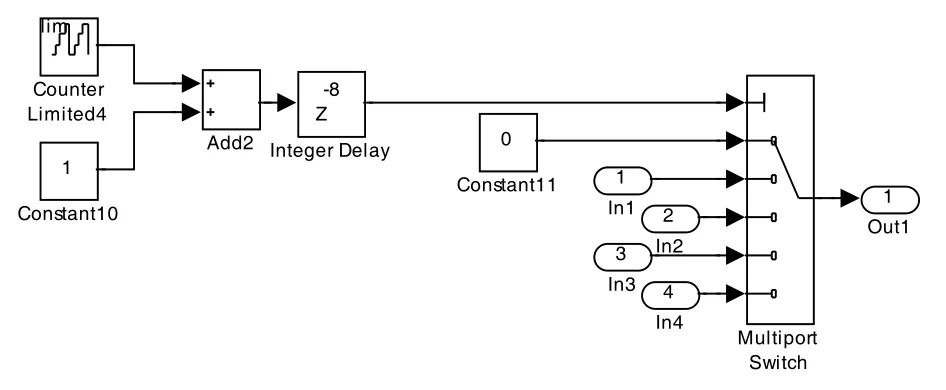
圖12 并串變換模塊

4 仿真結果分析

假設短波信道的中心頻率為3.001 5 MHz，信道帶寬為3 kHz，碼元持續時間為4 ms，時間帶寬積為12π，采樣頻率為20 M，調制路數分別為6 路和12 路，傳輸路徑為3 個，見表1，其中第1 徑為主徑。得到誤碼率和調制路數的關系如圖13 所示，可以看出，不同的信噪比條件，6 路調制時的誤碼率要明顯好于12 路調制時的誤碼率。這是因為調制路數增多時，PSWF 脈沖之間的正交性更易被破壞。短波信道的多徑時延、多普勒頻移、衰落以及噪聲等因素對傳輸信號正交性的影響加劇。PSWF 脈沖之間的正交性變差，解調端正是利用PSWF 脈沖正交性進行相關解調，所以系統的可靠性出現下降。

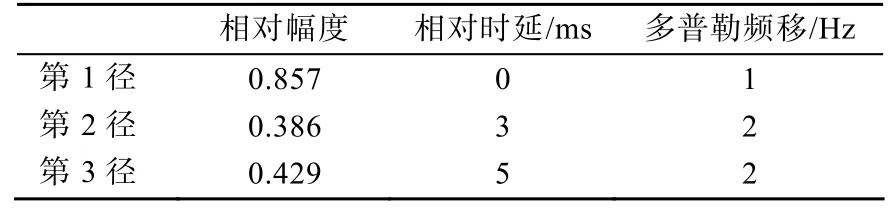
表1 信道參數

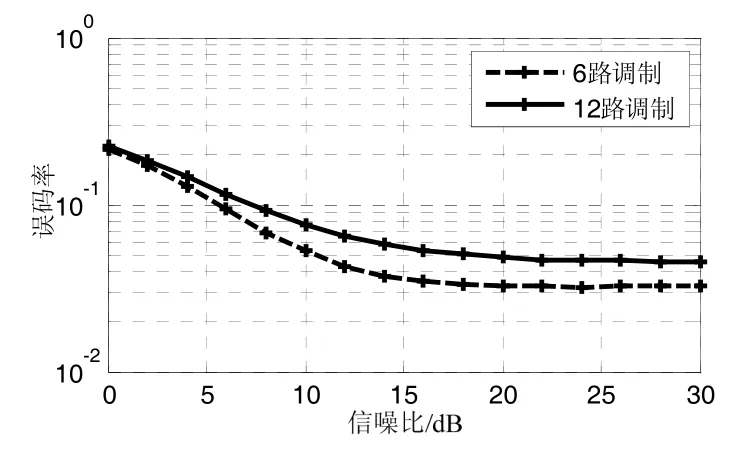
圖13 不同調制路數情況下誤碼率曲線

5 結論

利用Simulink 軟件對基于PSWF 的非正弦短波通信原理樣機實現之前的先驗性仿真，較真實地反映了基于PSWF 的非正弦通信技術在短波頻段內的特性。基于數據流的仿真，更加貼近原理樣機的實現，預先反映出了樣機實現中的問題。文中的重構方法可以完善地解決小相對帶寬PSWF 脈沖的實現問題。為下步原理樣機的實現提供了有力的支撐。

[1] 胡中豫. 現代短波通信[M]. 北京∶ 國防工業出版社, 2005∶1-7.

[2] 涂旭東. 寬帶短波信道特性和建模研究[D]. 成都∶ 電子科技大學, 2004∶2-3.

[3] 舒根春. 基于橢圓球面波的非正弦通信研究[D]. 煙臺∶ 海軍航空工程學院, 2011∶1-3.

[4] 張傳浩, 程健慶, 陳利風. 短波信道模型仿真實現及改進算法研究[J]. 指揮控制與仿真, 2009,31(6)∶76-78.

[5] 高瓏. 短波寬帶并行傳輸體制的研究[D]. 西安∶ 西安電子科技大學, 2009.

[6] 吳施其, 朱立東. 通信系統概論[M]. 北京∶ 清華大學出版社, 2005∶43-45.

[7] XIAO H, ROKHLIN V, YARVIN N. Prolate spheroidal wave functions, quadrature and interpolation[J]. Inverse Problems, 2001,17(4)∶805-838.

[8] REZA S DILMAGHANI, MOHAMMAD GHAVAMI, BEN ALLEN, et al. Novel UWB pulse shaping using prolate spheroidal wave functions[C]//14th IEEE International Symposium on Personal, Indoor & Mobile Radio Communication Proceedings. 2003∶602-606.

[9] KEDAR KHARE, NICHOLAS GEORGE. Sampling theory approach to prolate spheroidal wave functions[J]. Journal of Physics A∶ Mathematical and General, 2003(36)∶10011-10021.

[10] KEDAR KHARE. Bandpass sampling and bandpass analogues of prolate spheroidal functions[J]. Signal Processing, 2006(86)∶1550-1558.

[11] PARR B, CHO B, WALLACE K. A novel ultra- wideband pulse design algorithm[J]. IEEE Communica- tion Letters, 2003,7(5)∶219-221.

[12] 劉錫國, 王紅星, 劉傳輝, 等. 基于重構濾波的非正弦時域正交調制方法實現[J]. 吉林大學學報, 2012, 42(2)∶506-507.