用細分螺線插值容許G2Hermite數據
鄧重陽
(杭州電子科技大學理學院,浙江 杭州 310018)
用細分螺線插值容許G2Hermite數據
鄧重陽
(杭州電子科技大學理學院,浙江 杭州 310018)
為使幾何細分方法生成的平面螺線段插值平面容許G2Hermite數據,基于平面雙圓弧插值理論提出了該方法首末端點處新的細分規則。理論分析表明,修改后的細分方法所得極限曲線是曲率單調、不變號的螺線段,且插值首末端點處的點、切向、曲率。數值算例表明,修改后的細分方法收斂速度較快,極限曲線具有較好的形狀。
平面螺線;容許G2Hermite數據;Hermite插值
螺線段是曲率單調上升或下降且不變號的曲線。因為不含曲率極值點和尖點,螺線段被認為是光順曲線[1]。螺線設計在數學上的重要性體現于它在工程設計領域[2]及美學領域[3]中的重要應用上。
為了使兩段螺線段在連接點處達到G2連續,設計螺線時要求螺線段能插值兩端點及兩端點處的切向、曲率,即要插值兩點G2Hermite數據。螺線段只能插值特定的兩點G2Hermite數據,稱為容許G2Hermite數據。Meek和Walton用回旋螺線和一段圓弧[4]、一段指定的螺線和一段圓弧[5]插值容許 G2Hermite數據。Ait Haddou和Biard[6]用一對畢達哥拉斯曲線(Pythagorean Hodograph 曲線,簡稱PH曲線)的漸開線所形成的螺線來插值容許G2Hermite數據。Kuroda和Mukai[7]則用圓弧段的漸開線所形成的螺線來插值 G2Hermite數據。近年來,用(有理)Bezier曲線[8-9]和 PH 曲線[10-13]構造螺線來插值容許G2Hermite數據成為一個研究熱點。但據我們所知,還沒有文獻涉及用細分方法所得螺線段插值容許G2Hermite數據的問題。
用插值型細分方法構造插值曲線曲面是計算機輔助幾何設計中一種重要的造型方法。它具有算法簡單、適用于多分辨率造型等諸多優點。但與參數曲線曲面插值方法、隱式曲線曲面插值方法等造型方法相比,插值型細分方法所得插值曲線曲面的質量難以保證,且形狀難以控制。例如,以四點插值細分法[14]為代表的線性細分方法受人為痕跡、多余拐點等不良現象所困擾,而以基于幾何特征為代表的非線性插值型細分方法[15-16]則連續階不高,且其收斂性的證明較為復雜。最近,我們提出了生成螺線段的幾何細分方法[17],但該方法只能匹配G1Hermite數據。本文在該方法的基礎上,基于雙圓弧插值的理論修改其端點處的細分規則,使該方法生成的螺線能插值給定容許G2Hermite數據。
1 記號及背景知識
1.1 記號及初始假設
本文中,逆時針方向旋轉的角為正角,順時針方向旋轉的角為負角。點 pk與 pk之間的距離ii+1記為或
因為本文所得插值曲線為曲率不變號的螺線,不失一般性,我們假定所有初始給定的角都是正角。
1.2 容許G2Hermite 數據
G2Hermite數據記為(A, T ,κ ;B,T ,κ ),也
AA BB可記為(A, TA,OA;B, TB,OB),其中TA,TB為 A,B兩點處的單位切向量, κA,κB分別為 A,B兩點處的曲率, OA,OB分別為 A,B兩點處曲率圓的圓心。若記 rA= 1/κA,rB= 1/κBA,B兩點處曲率圓的半徑,則不失一般性,我們可以假定 κA> κB≥ 0。
給定G2Hermite數據{A, TA,κA;B,TB,κB},記αA,αB分別為從 TA到AB 和從AB到 TB的角。若κA> κB≥ 0,則{A ,TA,κA;B,TB,κB}為容許G2Hermite數據,即存在螺線插值它的充要條件[12](如圖1所示)。
1) αA> αB>0
2) 圓 OA(以 OA為圓心,為半徑)內含于圓 OB(以 OB為圓心,為半徑)。
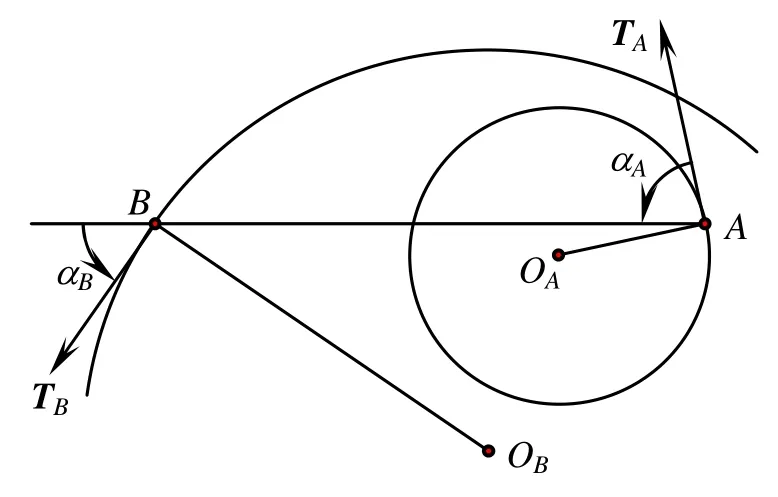
圖1 容許G2Hermite數據
1.3 雙圓弧
設A,B為相異兩點,TA,TB為A,B 兩點處的單位切向。記從TA到AB的角為 αA,從AB到TB的角為 αB。令O為插值 A,B兩點且對弦AB的張角為 π? (αA+ αB)/2的圓弧段,如圖2中的虛線所示圓弧段,則雙圓弧的連接點在且只在圓弧段O上[18]。令J為雙圓弧的連接點,T為J點處兩圓的公共切向量,θ為從TA到T 的角,為了控制雙圓弧的形狀,一般取θ為控制雙圓弧曲線的自由參數。
如果 αA,αB同號,則插值A,B兩點,TA,TB兩切向的雙圓弧為C形,否則為S形。由于本文考慮螺線插值,所以只討論C形雙圓弧。對于自由參數θ,在大部分情況下,θ = α是一個比較合適的選擇[19],如圖2所示。

圖2 平面C形雙圓弧

由以上兩式易知, rL,rR都是關于θ的減函數[18]。所以我們有
引理 1 對于G1Hermite數據{A, TA;B,TB},TA到AB的角記為α,AB到 TB的角記為β,且α > β,插值{A, TA;B,TB}的雙圓弧連接點所在圓弧段為O。 P1,P2為圓弧段O上的兩點。若∠ AOP1<∠ AOP2,則rR(P1) <rR(P2),rL(P1) < rL(P2)。
引理 2 容許G2Hermite 數據
(A, TA,κA;B,TB,κB)中,若 κA> κB≥ 0,則在插值(A, TA;B,TB)的雙圓弧中,存在以P為連接點的雙圓 弧 使 得 rB> rL(P )> rR(P )>rA。 這 里rA= 1/κA,rB=1/κB。
證 明 令圓 OA,圓 OB(圓心分別為 OA,OB)是 A,B兩點處的曲率圓。
容許G2Hemite 數據(A, TA,κA;B,TB,κB),由κA> κB≥0得0 < αB< αA。
記O為插值A,B兩點且對線段AB的夾角為 π? (αA+ αB)/2的圓弧(圖3中虛線所示圓弧段)。記O在點A處的切向量為 TCA,則從 TCA到AB的角為(αA+ αB)/2。所以圓O與圓 OA有兩個交點。顯然A為圓C與圓 OA的一個交點。記圓O與 OA的另外一個交點為 A',由(αA+αB)/2<αA可知, A'在 A, TA,AB所確定區域內。同理,圓O與 OB除了交點B之外,還有一個交點 B',且 B'在B, ?TB,BA所確定的區域內,如圖3所示。
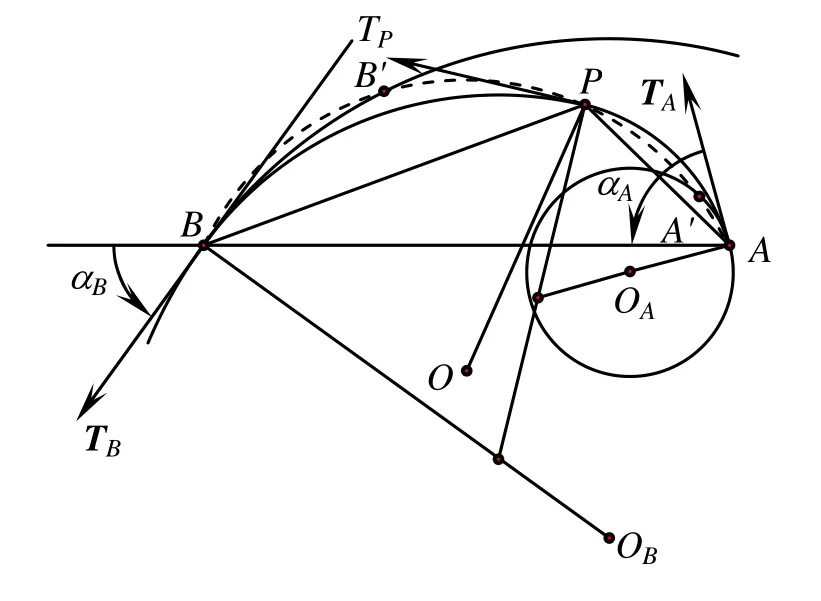
圖3 滿足半徑單調條件的雙圓弧
由κA> κB≥ 0知 OB內含于 OA,所以 B' 介于 A',B之間。設P為圓弧段O上介于 A'B'的一點,以P為連接點且插值(A, TA;B,TB)的雙圓弧的半徑分別為 rR(P),rL(P ),由引理 1可得rB> rL(P ) > rR(P )>rA。證畢。
2 細分方法
給定初始的容許G2Hermite數據 {p00,T00,O00; p0,T0,O0},在第 k個細分步驟中,我們保持老11 1頂點不變,但老頂點重新標記為 pk+1= pk,在每兩個老頂點 pik,pik+1之間根據兩點 pik,pik+1及其切向(在端點處還要用到曲率信息)插入一個新點,并對新點列的每一個點定義一個切向使細分進行下去。下面我們分別闡述加入新點的規則及確定切向的規則。
2.1 加入新點的規則
我們把加入新點的規則按相鄰兩點是否為端點分為3類:相鄰兩點都是端點;相鄰兩點都不是端點;相鄰兩點有一個是端點。下面分別介紹這3類確定新點的規則。
2.1.1 相鄰兩點都是端點
實際上,這種情況只在第1步細分的時候出現。此時,對于初始的容許 G2Hermite數據確定點 p1的方法是:1
設插值 p00,p10兩點且對線段 p00p10張角為π? (α + β)/2的圓弧段為O,其圓心記為O(圖4中虛線所示圓弧段),圓 O00(圓心為 O00,半徑為與圓弧段O的交點為 A'; 圓 O0(圓心為1 O10,半徑為與圓O的交點為 B'。∠ A'OB'的平分線與圓弧段O的交點即為 p11。
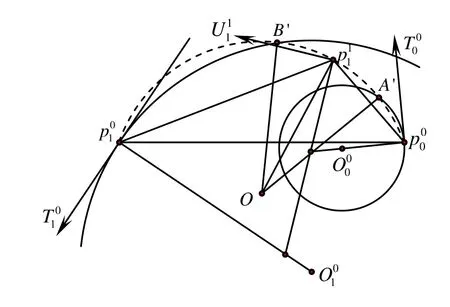
圖4 相鄰兩點都是端點時的加入新點規則
2.1.2 相鄰兩點都不是端點
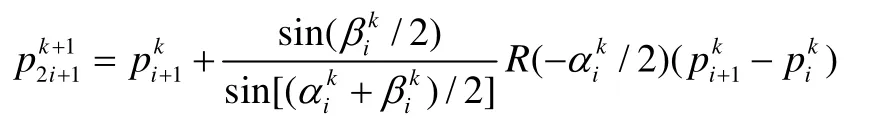
2.1.3 相鄰兩點有一個是端點
這種情形實際上還可以分成兩種情況:pk,pk為 pk,pk或 pk,pk。這兩種情況下的規ii+1012k?12k則是完全類似的。
1) pik,pik+1為 p0k,p1k
否則,令 p1k+1為插值的雙圓弧的連接圓弧上滿足以下條件的點
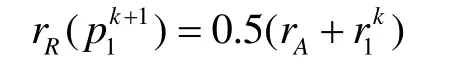
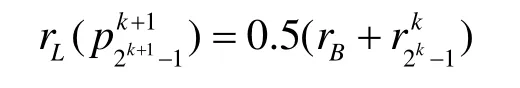
2.2 確定切向的規則
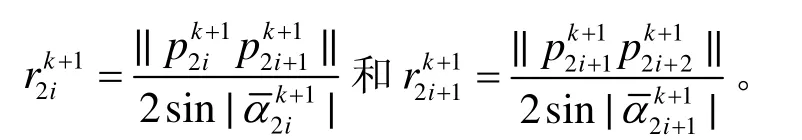
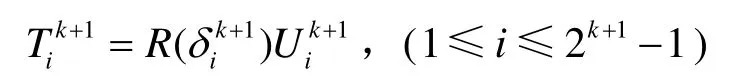
其中

3 光滑性分析
文獻[17]已經證明了生成平面螺線的幾何細分方法的收斂性和光滑性。由于本文算法僅對端點處的規則做了修改,所以只要對端點說明其收斂性和光滑性即可。
定 理 第1節所定義的細分方法細分容許G2Hermite數據所得極限曲線是插值的平面螺線。
證 明 與文獻[17]相同的方法可以證明極限曲線的收斂性、G1、G2連續性以及極限曲線是螺線。在這里我們僅證明極限曲線插值容許G2Hermite數據的兩個端曲率即可。
由第3.1節的加入新點規則可知,
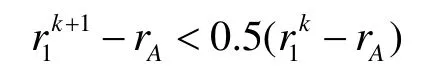
所以極限曲線插值兩個端曲率,證畢。
4 數值算例
我們已在很多實例中檢驗了本文算法,本節給出 4個有代表性的數值算例。所有實例中,對于每一個實例,我們畫出了7個細分步驟后的離散點列,如圖5中各圖的藍色實線及其離散曲率,如圖5中各圖的紅色實線,每個離散點列有257個點。為了更好地了解極限曲線的性質,我們在圖中畫出每個點的離散曲率,如圖5中紅線,其長度為實際曲率的0.2倍,即此點及附近三點所確定的圓在此點處的曲率。令點 pk處的離散曲率為 κk,記ii我們在表1中給出了每個細分步驟后的 Dk及從表1可知,基本上處于0.5至0.8之間,所以相鄰兩點間的離散曲率之差以較快的速度趨向于0。

表1 每個細分步驟后 Dk, Dk /Dk?1的變化情況
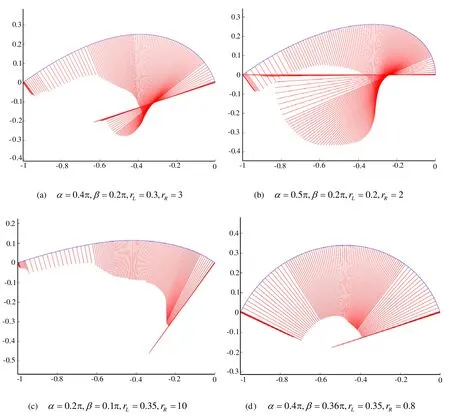
圖5 細分實例
5 結 論
本文介紹了一種用幾何細分方法生成的螺線插值容許 G2Hemite數據的方法。其方法僅在第一步細分規則及兩端點處的細分規則做了修改,其余點處的細分規則與生成螺線段細分方法完全相同。理論分析表明,本文所述細分方法所得點列收斂于一條螺線段,且插值兩端點處的G2Hermite數據; 數值算例表明,其算法運算穩定,收斂速度較快。
[1] Farin G. Curves and surfaces for computer aided geometric design [M]. A Practical Guide, fourth ed., Academic Press, San Diego, 1997: 364.
[2] Gibreel G M, Easa S M, Hassan Y, et al. State of the art of highway geometric design consistency [J]. Journal of Transportation Engineering, 1999, 125(4): 305-313.
[3] Burchard H G, Ayers J A, Frey W H, et al. Approximation with aesthetic constraints [M]. Designing Fair Curves and Surfaces, SIAM, 1994: 3-28.
[4] Meek D S, Walton D J. Clothoid spline transition spirals [J]. Mathematics of Computation, 1992, 59: 117-133.
[5] Meek D S, Walton D J. Planar spirals that match G2hermite data [J]. Computer Aided Geometric Design, 1998, 15: 103-126.
[6] Ait H R, Biard L. G2approximation of an offset curve by Tschirnhausen quartics [C]//Dahlen M, Lyche T, Schumaker LL (Eds), Mathematical Methods for Curves and Surfaces. Vanderbilt University Press, 1995: 1-10.
[7] Kuroda M, Mukai S. Interpolating involute curves[C]// Cohen A, Rabut C, Schumaker LL. Curve and Surface Fitting, Saint Malo, 1999. Vanderbilt University Press, Nashville, 1999: 1-8.
[8] Frey W H, Field D A. Designing Bezier conics segments with monotone curvature [J]. Computer Aided Geometric Design, 2000, 17(6): 457-483.
[9] Dietz D A, Piper B. Interpolation with cubic spirals [J]. Computer Aided Geometric Design, 2004, 21(2): 165-180.
[10] Habib Z, Sakai M. On PH quintic spirals joining two circles with one circle inside the other [J]. Computer Aided Design, 2007, 39(2): 125-132.
[11] Habib Z, Sakai M. G2Pythagorean hodograph quintic transition between two circles with shape control [J]. Computer Aided Geometric Design, 2007, 24(5): 252-266.
[12] Walton D J, Meek D S. G2curve design with a pair of pythagorean hodograph quintic spiral segments [J]. Computer Aided Geometric Design, 2007, 24(5): 267-285.
[13] Goodman T N T, Meek D S, Walton D J. An involute spiral that matches G2Hermite data in the plane [J]. Computer Aided Geometric Design, 2009, 26(9): 733-756.
[14] Dyn N, Levin D, Gregory J A. A 4-point interpolatory subdivision scheme for curve design [J]. Computer Aided Geometric Design, 1987, 4(4): 257-268.
[15] Yang Xunnian. Normal based subdivision scheme for curve design [J]. Computer Aided Geometric Design, 2006, 23(3): 243-260.
[16] 鄧重陽, 汪國昭. 曲線插值的一種保凸細分方法[J].計算機輔助設計與圖形學學報, 2009, 21(8): 1042-1046.
[17] Deng Chongyang, Wang Guozhao. Generating planar spiral by geometric subdivision scheme [J]. Science of China, Series F, Information Science. 2009, 52(10): 1821-1829.
[18] 蘇步青, 劉鼎元. 計算幾何[M]. 上海科學技術出版社, 1985: 195-204.
Spiral-preserving geo2metric subdivision scheme for admissible G Hermite interpolation
Deng Chongyang
( College of Science, Hangzhou Dianzi University, Hangzhou Zhejiang 310018, China )
To interpolate admissible G2Hermite data, this paper proposes a modified geometric subdivision scheme with new subdivision rules near the end points of the curve. The method is based on the theory of planar biarc curve interpolation. Theoretical analysis shows that the limit curves of the modified subdivision scheme are planar spirals, which are curves of one-signed, monotone increasing or decreasing curvature. Numerical examples show that the modified subdivision scheme converge rapidly, and the limit curves are with nice shape.
planar spiral; admissible G2Hermite data; Hermite interpolation
TP 391
A
2095-302X (2012)02-0039-06
2011-09-29
國家自然科學基金數學天元青年基金資助項目(10926058,11026107);國家自然科學基金青年基金資助項目(61003194)
鄧重陽(1976-),男,湖南隆回人,副教授,博士,主要研究方向為計算機輔助幾何設計與圖形學。

