基于模糊層次分析法的可中斷負荷信用風險評估

王蓉蓉，趙 飛

（1.華北電網有限公司 培訓中心，北京 102445；2.懷柔供電公司，北京 懷柔 101400）

可中斷負荷管理（interruptible load management,ILM）的實施以用戶自愿為基礎，雙方簽訂合同，各自履行其權利和義務，如表1所示。如果用戶因故（生產計劃調整或缺電成本過高等）無法履行義務而選擇違約，須提前向電力公司提出申請，以便重新安排調度和發電計劃。電力公司在與用戶簽訂可中斷合同之前，要對用戶的信用風險進行評估，以篩選出更理想的用戶。

表1 可中斷合同雙方的權利和義務

由于用戶信用風險評估中包含有很大的不確定性和模糊性，本文中采用廣義模糊層次分析法計算權重。FAHP是層次分析法（analytic hierarchy process,AHP）的提高，彌補了AHP在專家使用1—9標度比較重要性方面的不確定性，應用模糊數學中的三角模糊數（triangular fuzzy number,TFN）得到成對比較矩陣，并運用模糊綜合評價法來計算最終權重。此外，傳統評估方法是建立在精確歷史數據的基礎上，而ILM中的信用風險評估是針對未來事件，具有許多可能價值，因此系統使用的方法需要包括這些可能性。本文利用概率論解決這一問題，為管理者提供更為現實的選擇。

1 模糊層次分析法

1.1 層次分析法

層次分析法主要應用在社會、經濟以及科學管理領域問題的系統分析中，是面臨一個由相互關聯、相互制約的眾多因素構成的復雜而缺少定量數據的系統時，可以提供的一種簡潔而實用的建模方法，可按下面4個步驟進行。

（1）建立遞階層次結構模型

分析決策問題時，需要構造出一個有層次的結構模型，將有關因素按照不同屬性自上而下地分解成若干層次，整體上分為目標層、準則層和方案層。

（2）構造各層次中的判斷矩陣

AHP的特點在于當影響某因素的因子較多時，使用兩兩重要性程度之比的形式表示出2個因子的重要性程度等級，使用“同等重要”、“稍微重要”、“明顯重要”、“十分重要”、“極其重要”等定性語言，并引入函數f(x,y)表示對總體的重要性標度，如表2所示。

表2 比較重要性的離散1—9標度

設x={x1,x2,…,xn}是全部因素的集，按表2對全部因素作兩兩對比，構建比較矩陣A=(aij)n×n，其中aij=f(xi,xj)。

（3）層次單排序及一致性檢驗

判斷矩陣A對應于最大特征值λmax的特征向量W，經歸一化后即為同一層次相應因素對于上一層次某因素相對重要性的排序權值，這一過程稱為層次單排序。為保證比較結果前后完全一致，矩陣A的元素還應滿足

式中：i，j，k=1，2，…，n。需要檢驗構造出來的（正互反）判斷矩陣A是否嚴重地非一致，以便確定是否接受A。

對判斷矩陣的一致性檢驗的步驟如下：

步驟一：計算一致性指標CI。

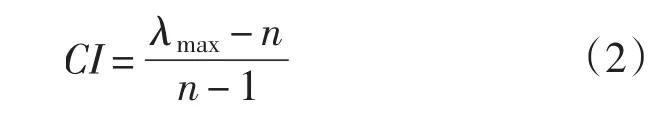
步驟二：查找相應的平均隨機一致性指標RI。RI的值可通過隨機方法構造500個樣本矩陣：隨機地從1—9及其倒數中抽取數字構造正互反矩陣，求得最大特征根的平均值λ'max，并定義

當CR＜0.10時，認為判斷矩陣的一致性是可以接受的，否則應對判斷矩陣作適當修正。

（4）層次總排序及一致性檢驗

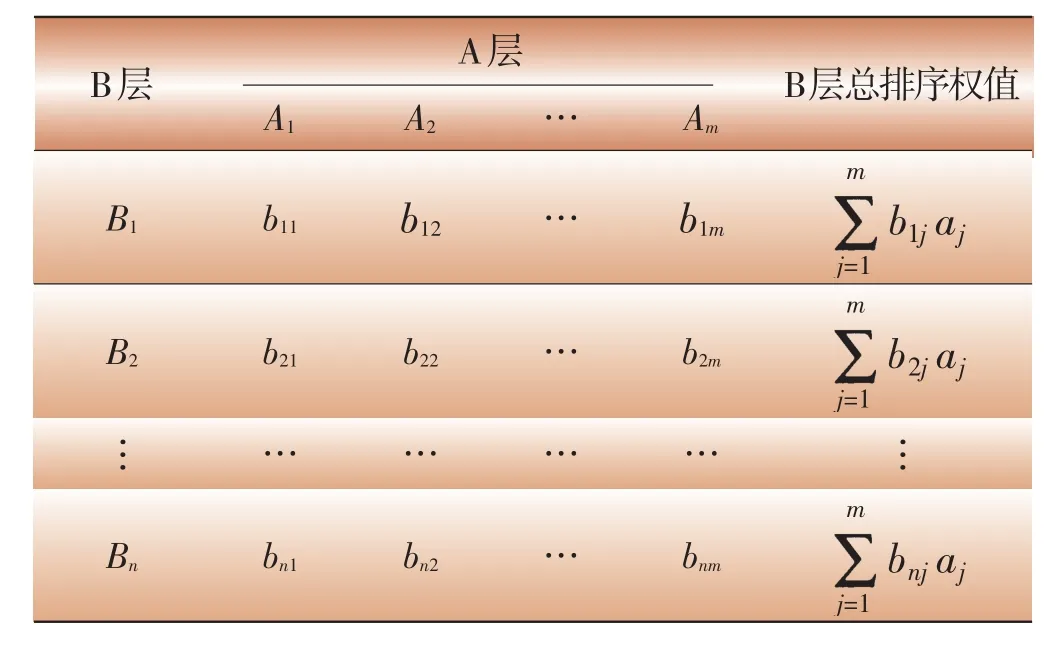
表3 B層各因素的層次總排序權重

1.2 模糊層次分析法的改進

AHP所使用的離散1—9標度沒有考慮到人判斷的主觀模糊性，不能處理在決定不同指標屬性上的不確定性和模糊性，很可能受到打分者主觀判斷的影響，與實際情況偏差較大。

考慮到ILM受氣候、經濟、社會等不確定因素的影響較大，不同評估指標之間的相關性判斷包含了很大的主觀判斷和個人喜好，傳統AHP的離散1—9標度不能充分的處理ILM指標在數字的映射上的不確定性。此時，區間判斷比固定價值判斷更具信服力。因此，采用FAHP中的TFN來決定指標變量的比較重要性，并以此為基礎來確定決策變量較其他變量的優先權，這種綜合評價方法即為模糊層次分析法。

1.2.1 模糊數的概念

設N為實數論域R上的一個模糊集，若λ∈［0,1］，Nλ是R中有限閉區間，則稱N為R上的一個模糊數。

1.2.2 三角模糊數的概念及計算

一個典型的三角模糊數如圖1所示。其中n1、n2、n3分別表示最小可能值、峰值和最大可能值。若N的隸屬函數為uN，滿足

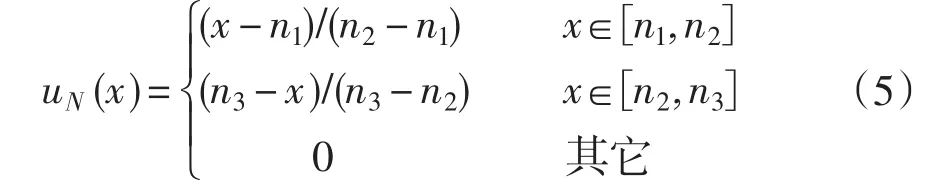
式中：n1≤n2≤n3，則稱N為三角模糊數，記作(n1，n2，n3)。

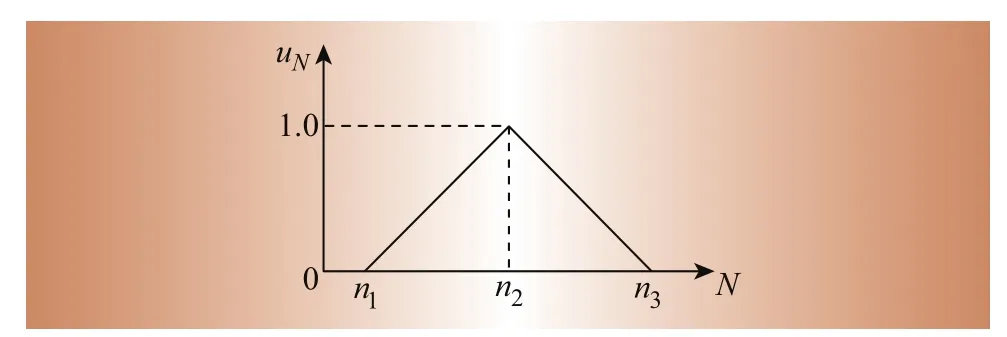
圖1 三角模糊數

1.2.3 三角模糊比較矩陣

由TFN取代AHP中的離散1—9標度來比較2個指標之間的相關重要性，所建立的模糊比較矩陣如表4所示。

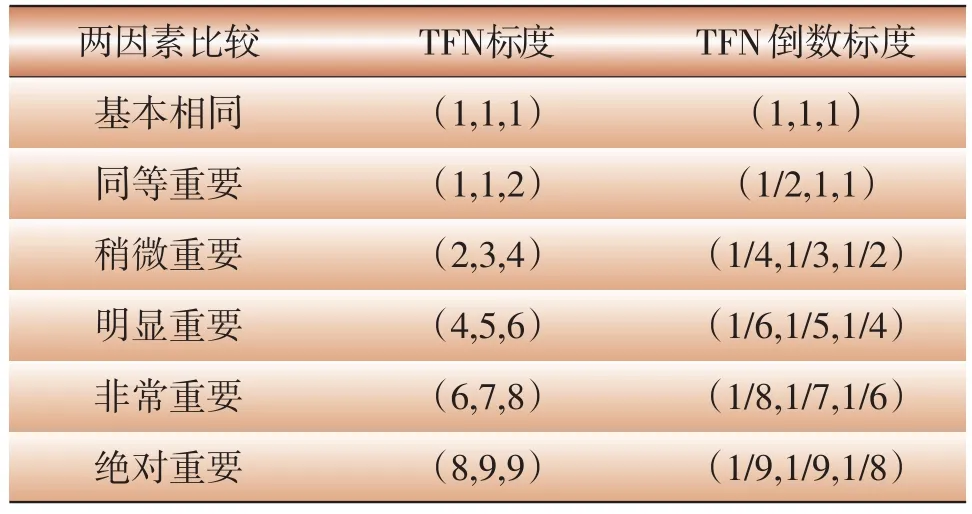
表4 三角模糊比較矩陣

2 ILM信用風險評估指標體系

通常來講，在電力公司與用戶簽訂了ILM合同后，在某一時刻用戶認為可中斷成本過高而無法承受時，將會訴諸于違約。因此可知，ILM用戶的信用風險與其機會成本呈正相關關系，機會成本越大，用戶的信用風險越大。按照AHP的步驟，將指標體系建立如圖2所示。

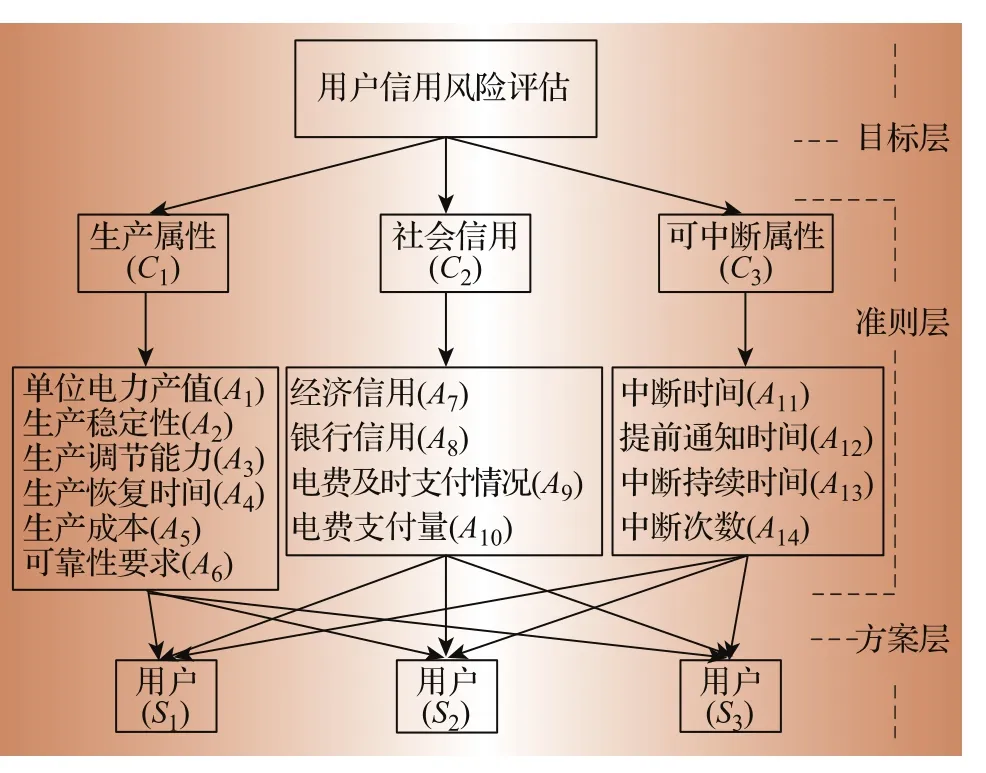
圖2 ILM信用風險評估指標體系

在確定指標體系各層次之后，應根據上述三角模糊數的判斷方法分別對各層次的指標進行兩兩比較，得到ILM模糊判斷矩陣，并計算各指標的權重。

3 信用風險綜合評價

3.1 單層次指標權重計算

對準則層的各層次指標進行權重計算，得到單層次的各指標權重。根據三角模糊數和模糊判斷矩陣的定義，令x（x1，x2，…，xn）為一個評估指標，則xi（i=1，2，…，n）與其他指標相比的相關重要性能通過專家的判斷獲得，并由TFN表示如式（6）所示

基于FAHP的指標權重計算步驟如下：

（1）針對每個用戶，對第i個指標進行單因素分析，可得用戶的第i個指標相對其他指標的綜合TFN

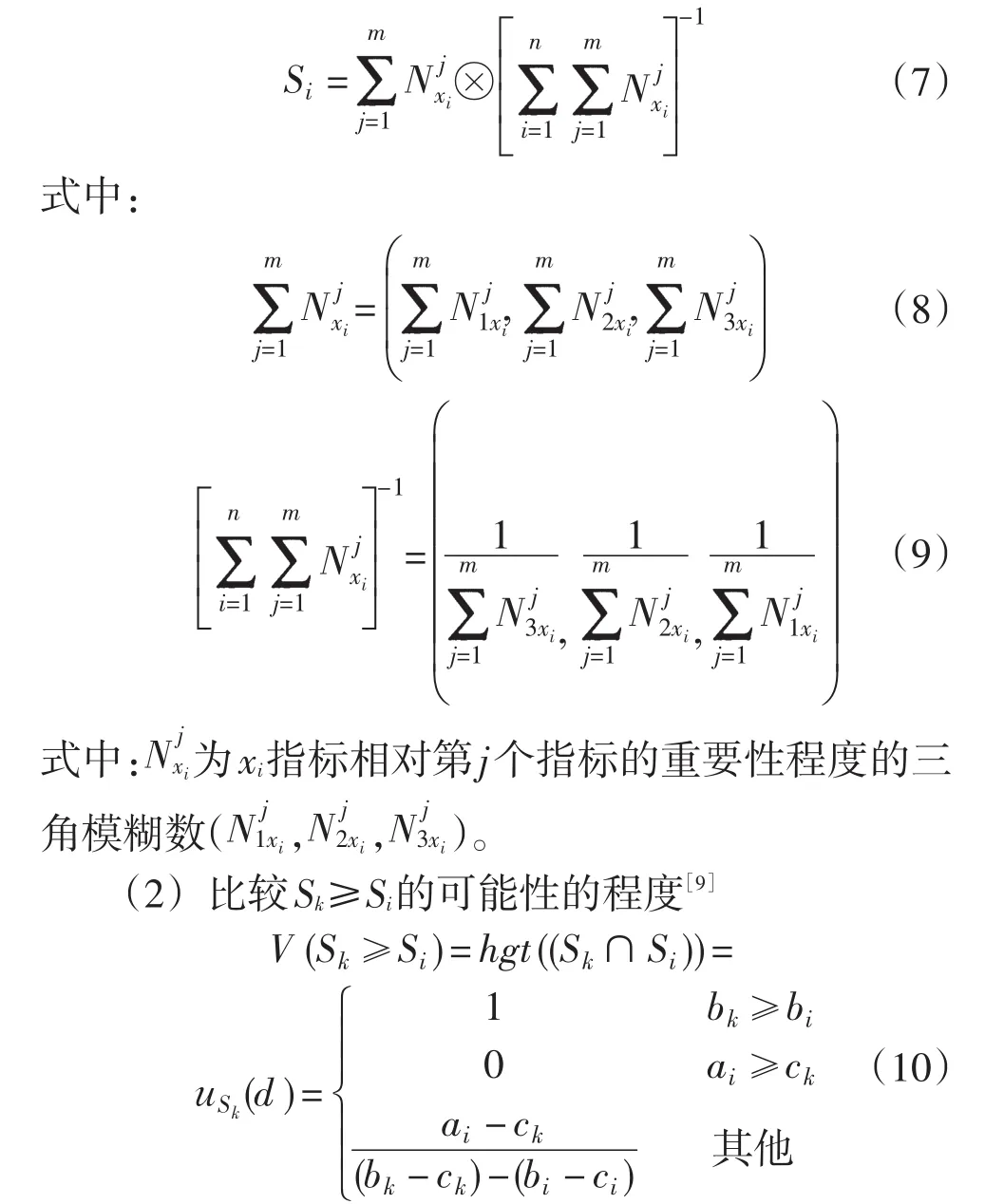
式中：a、b、c分別是TFN Sk和Si的3個參數；d為uSk和uSi的交點處的橫坐標，如圖3所示。

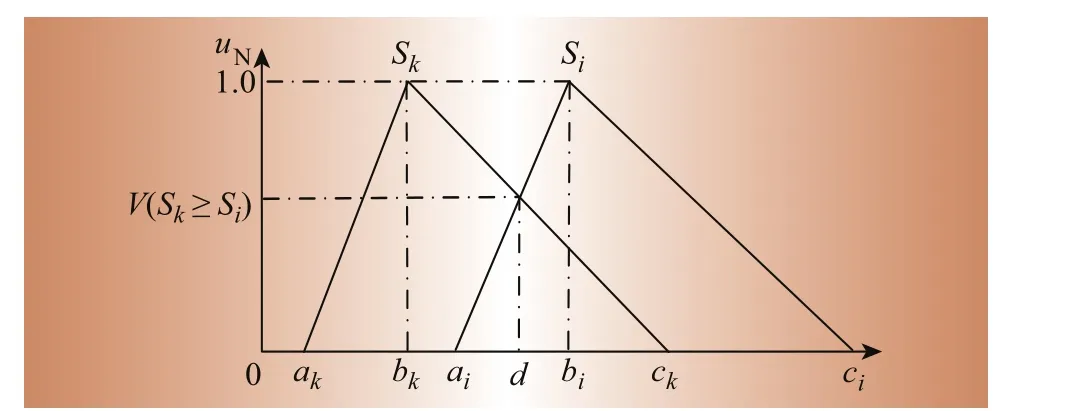
圖3 Sk和Si比較

（3）模糊數Si大于其他所有模糊數Sk的可能性的程度

V（Si≥S1，S2，…，Si-1，Si+1，…，Sn）=min V（Si≥Sk）（11）式中：i、k=1，2，…，n，且i≠k。

（4）計算第i個指標在準則層C中的指標權重

通過FAHP計算得到的ILM信用風險評估體系的單層次指標權重

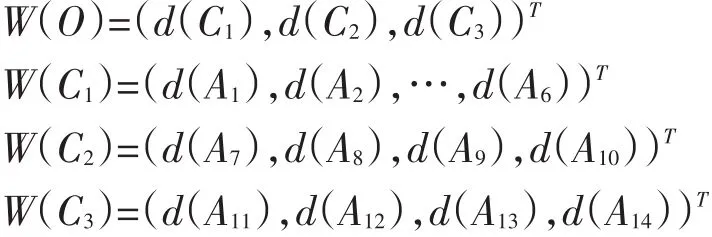
3.2 多層次模糊綜合評價法

考慮到同一個因素對不同用戶的信用風險貢獻程度不同，建立了模糊評價矩陣，最后通過模糊傳輸得到了目標層對于所有用戶的綜合評價。

（1）根據指標體系的構建層次，對因素集合進行劃分，將其分成如式（15）所示的4個子集，每個子集表示了對象所具有的屬性。

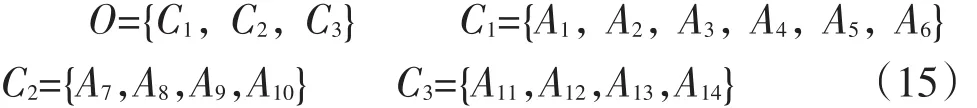
（2） 就每個子集 C1、C2、C3中的 Ai因素，作單因素評價。因為同一個因素對不同用戶的信用風險貢獻程度不同，首先要構建單因素評價矩陣。

對于每個因素Ai，都會有一個模糊評價Ri={ri1，ri2，…，rij}，rij為參與ILM信用風險評估的第i個用戶相對于第j個用戶的三角模糊數，因此可構建出單因素評價矩陣

若已知模糊評價矩陣R和因素的權重分配W，則可由R和W求得模糊綜合評價B，即得到了用戶相對于該層次指標的綜合評價。這一運算可寫成

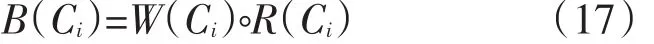
式中：“?”代表合成運算。

在廣義模糊運算下B的各元素

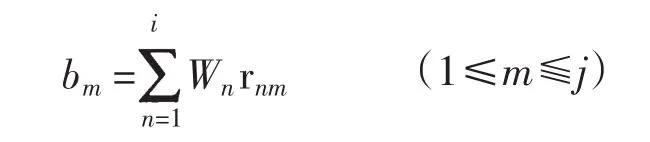
（3）把每個Ci作為一個因素，B（Ci）作為Ci的單因素評價。O={C1，C2，C3}，按步驟（2）中的方法進行綜合評價，得

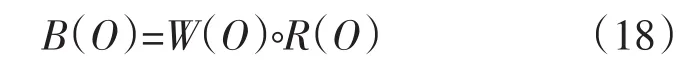
由此得到用戶相對于目標層的綜合評價結果。

4 算例分析

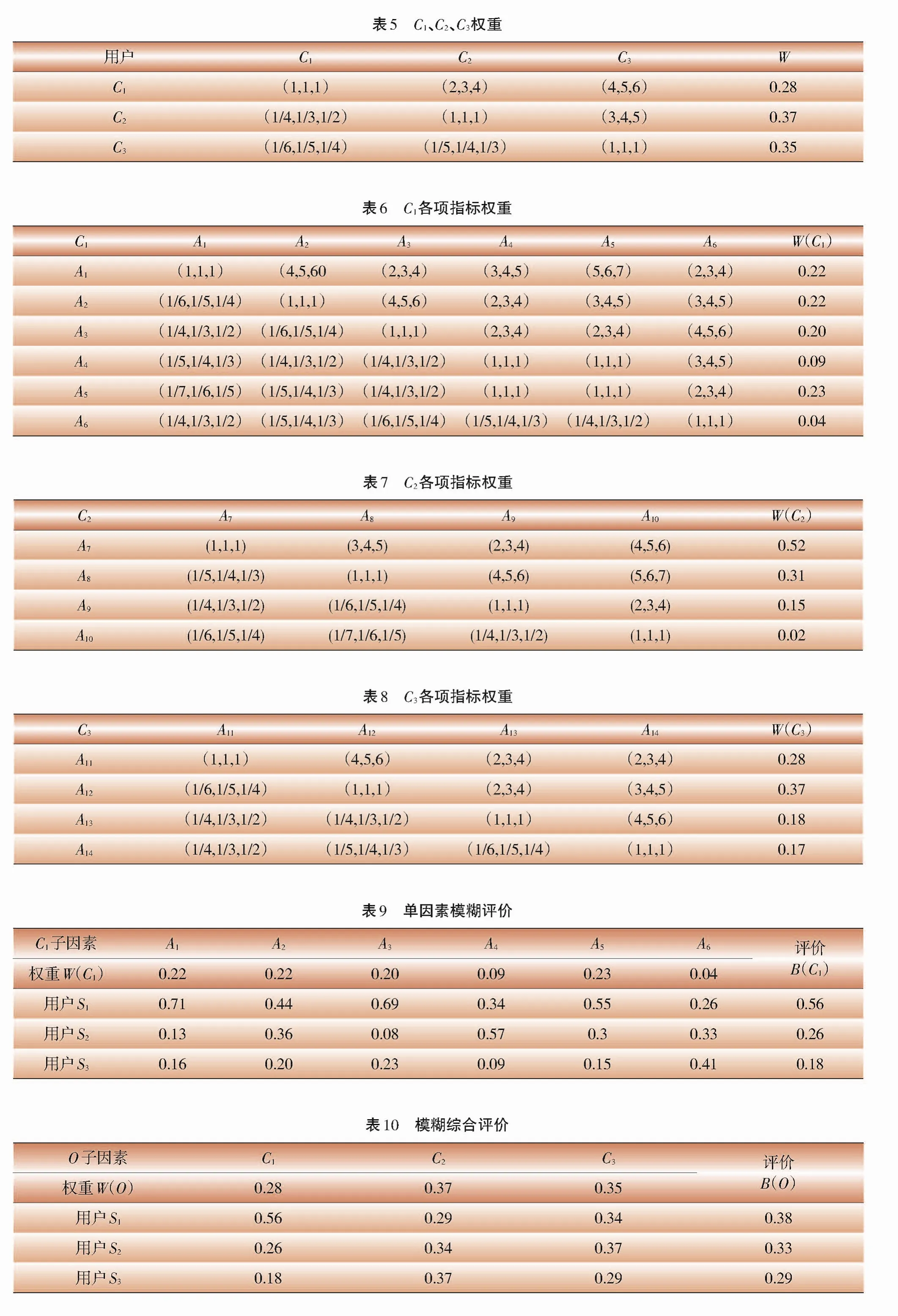
假設某地區有3個用戶符合參與ILM的基本條件，S1用戶為外資電子加工基地，S2用戶為國營紡織廠，S3用戶為民營礦業集團，現需要對其信用風險進行評估排序。依據圖2中給出的指標體系，專家給出各指標重要性程度比較數據，原始參數見表5—表8中三角模糊數，通過計算得出各層指標權重。

對每個子集因素做單因素評價，以C1為例，建立如下模糊評價矩陣R（C1），如表9所示。權重W（C1）已由表6得出，根據公式（17），得到C1子集因素的評價值B（C1）。

同理可得到C2、C3的單因素評價B（C2）=（0.29,0.34,0.37），B（C3）=（0.34,0.37,0.29）。

將單因素評價所得作為一個單因素進行分析，得到目標層O對3個用戶的綜合評價，見表10。

通過模糊綜合評價，最后可得3個用戶的信用風險權重B（O）=（0.38，0.33，0.29），風險從大到小排序為（S1，S2，S3）。

5 結束語

本文首先建立了可中斷用戶信用風險指標體系，接著應用模糊層次分析法得到基于三角模糊數的專家判斷矩陣，解決了專家在判斷兩兩指標相關重要性方面的不確定性。然后對用戶進行信用風險的綜合評價，包括單層次指標權重計算和多層次模糊綜合評價，從而對所有用戶進行權重排序，篩選出風險較小的用戶參與到可中斷負荷管理當中。最后的算例通過對3個擬參與可中斷負荷管理的用戶進行風險評估，驗證了該機制的有效性。

［1］ 王蓉蓉.可中斷負荷管理的激勵機制研究[D].北京：北京交通大學,2008．

［2］ 王建學,王錫凡,王秀麗.電力市場可中斷負荷合同模型研究[J].中國電機工程學報,2005,25(9)：11-16．

［3］ 王建學,王錫凡,王秀麗.電力市場和過渡期電力系統可中斷負荷管理(一)：可中斷負荷成本效益分析[J].電力自動化設備,2004,24(5)：15-20．

［4］ 方勇,李渝曾.電力市場中激勵性可中斷負荷合同的建模與實施研究[J].電網技術,2004,28(17)：16-22．

［5］ 周渝慧,王建功.企業工程經濟學[M].北京：中國科學技術出版社,1993．

［6］ 趙學順,余志偉,鐘志勇,等.基于高峰負荷定價理論的運行備用獲取和定價[J].電力系統自動化，2003，27(2)：24-28．

［7］ 王治華,李博,李揚.電力市場下的可中斷負荷管理及其方法[J].中國電力,2003,36(6)：21-27．

［8］ 王蓉蓉,周渝慧,師睿.可中斷負荷管理激勵機制的設計[J].電力需求側管理,2008(1)：12-15．

［9］ Zadeh L A.Fuzzy sets[J].Information and control,1965,8（3）：338-353．