基于稀疏表示及光譜信息的高光譜遙感圖像分類

宋相法 焦李成(西安電子科技大學智能感知與圖像理解教育部重點實驗室 西安 710071)

②(河南大學計算機與信息工程學院 開封 475004)

1 引言

高光譜遙感圖像是由幾十乃至數百個連續波段圖像組成的3維數據立方體，具有“圖譜合一”的特點，提高了對地物的分類和監測能力，已經被廣泛應用于資源勘探、環境監測、精細農業、災害評估、目標識別等領域[1-5]。像元分類是高光譜遙感圖像研究的最重要內容之一。由于硬件等因素的制約，高光譜遙感圖像的光譜空間分辨率高而空間分辨率往往相對較低，如果僅利用光譜信息進行分類，其分類精度必然受到一定的制約。為了提高像元分類精度，必須進一步提取圖像的其他信息，例如形狀、紋理、空間關系和擴展形態剖面(extended morphological profile)特征[1]。另外，由于高光譜數據維數高、數據量大、訓練樣本數目有限，傳統的分類方法運算速度慢，分類精度低，還會出現嚴重的huges現象[6]。在高光譜遙感分類中隨機森林分類器[7]具有明顯的優越性，因此隨機森林分類器應用被歸納為高光譜遙感分類最重要的進展之一[4,5]。

由于光譜成像儀的空間分辨率限制以及自然界地物的復雜多樣性，通常情況下，高光譜圖像中每個像元往往包含幾種地物，可以認為是圖像中幾個端元的線性組合。最近發展起來的稀疏表示[8]就是把圖像表示為字典中基原子的稀疏線性組合。當把圖像投影到這些原子組成的特征子空間時，只有少部分同時處于活躍狀態，產生對該圖像的稀疏表示。該方法可以描述上述高光譜圖像像元的特性，并成功應用于高光譜混合像元分解[9]。

為了提高像元分類精度，本文提出了基于稀疏表示[8]的高光譜遙感圖像特征提取算法，結合稀疏表示特征及光譜信息，使用隨機森林方法[7]作為分類器，提出了一種新的高光譜遙感圖像分類算法。實驗結果表明：相對于光譜信息方法和稀疏表示特征方法，本文算法能夠提高高光譜遙感圖像分類的各項評價指標。

2 本文算法

由于稀疏表示模型符合生物視覺系統特性，且能夠提取圖像的高級特征[8]，成為了圖像處理和模式識別等領域的研究熱點[8-18]。本文利用稀疏表示提取高光譜圖像稀疏表示特征，基于稀疏表示特征及光譜信息利用隨機森林作為分類器提出了一種新的高光譜遙感圖像分類算法。

2.1 高光譜遙感圖像字典學習

如何獲得高光譜圖像中的端元構造字典是利用稀疏表示方法提取稀疏表示特征的關鍵問題。常用的端元提取方法主要有純像元指數，N-FINDR，定點成分分析和主分量分析，這些方法假設高光譜數據位于一個凸面體內[19]。而稀疏表示模型不需要假設數據位于凸面體內，利用學習的方法構造的字典原子更能有效地捕獲高光譜圖像像元的譜特征，該字典可以有效地表示像元。

令高光譜遙感圖像數據集X={xi|xi∈?m,1 ≤i≤n}，字典D∈?m×p(每一列Dj∈?m為一個原子)，該字典D能夠捕獲像元的譜特征，且每個像元xi可以被字典D中的原子稀疏線性表示。根據文獻[18]，可以把字典學習的問題轉化為求解如下形式的優化問題：

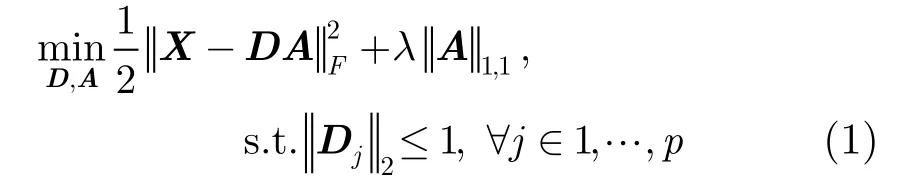
其中A∈?p×n為系數矩陣(每一列Ai∈?p為一個系數向量)，λ＞0。式(1)中第1項為重構誤差，第2項為稀疏懲罰函數，參數λ表示數據重構和稀疏性之間的折中關系。字典D中的元素Dj和系數矩陣A中的元素Ai是被優化的變量。

在字典學習階段，當字典D和系數矩陣A不固定時，上述問題不是凸優化問題。通常情況下，采用迭代的方法可以求解式(1)。首先固定字典D，則式(1)轉化為一個關于A的基于?1-范數的最小平方凸優化問題；然后固定系數矩陣A，則式(1)轉化為一個關于D的帶二次約束的最小平方凸優化問題。通過多次迭代求解可以得到字典D。

2.2 高光譜遙感圖像稀疏特征提取

利用2.1節學習得到的字典D，根據稀疏表示理論，可以把像元x∈X表示為字典D中原子的稀疏線性組合，即求解下列優化問題：

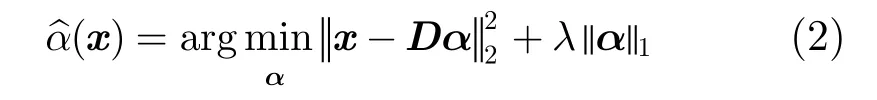
式(2)是一個凸?1-正則化最小平方問題，得到的解是一個稀疏向量，即只有少數元素不為零。

由于同類像元的光譜曲線結構非常相似，因此根據字典D求得的系數也比較相似。根據文獻[14]，可以把作為像元x的一種新的表示形式，即像元x在字典D上的稀疏表示特征。

2.3 隨機森林

利用高光譜圖像稀疏表示特征及光譜信息表示像元x∈X時，由于它們處于兩個不同的表示空間，為了提高分類精度，本文提出利用分類器集成方法。隨機森林是近年來比較流行的一種基于決策樹(decision tree)的分類器集成算法。該算法是一種對參數選擇不敏感，不存在過適應，分類結果穩定，學習訓練速度較快的分類器集成算法，在解決多類問題上具有許多獨特的優勢。隨機森林方法定義如下[7]：

隨機森林分類器由多個決策樹(h(x,θk),k=1,2,…,l)組成，其中θk是相互獨立且同分布的隨機向量，每個決策樹對于輸入給出獨立的分類結果，最終根據所有決策樹的分類結果通過多數投票決定輸出結果。

隨機森林算法包括兩部分，即構建l棵決策樹和投票決定分類結果。在構造決策樹時，采用bagging方法[20]，即從全體訓練樣本集中隨機地有放回地選取一個子集，作為單棵決策樹的訓練樣本集，上述過程重復l次就分別得到l棵決策樹的訓練樣本集。同樣，在每棵決策樹的生成過程中也引入了隨機性，若訓練數據為q維特征向量，在決策樹的每個節點處，并不對所有特征進行比較，而是隨機選擇t(t?q)個特征進行比較，選擇其中分類結果較好的特征來切分樹節點。引入隨機性使得每兩棵樹之間的差異度增加，從而使得森林的泛化誤差提高。構造的決策樹不進行剪枝。利用隨機森林方法進行分類的最終分類結果由所有決策樹通過多數投票決定。

由于隨機森林采用隨機子空間特征選擇方法減少了輸入空間的維數且能夠快速構造決策樹，同時根據多個決策樹的結果采用投票策略決定分類結果，因此能夠克服傳統高光譜數據分類方法中所面臨的數據維數高，訓練樣本數目少，運算速度慢等問題，有效地對高光譜數據進行分類。

2.4 算法步驟

本文提出結合稀疏表示特征及光譜信息，充分利用不同表示空間的特征信息，使用隨機森林方法對高光譜遙感圖像進行分類。算法步驟如下：

(1)字典學習。利用SPAMS工具箱[18]求解式(1)，得到學習字典D。

(2)特征提取。利用SPAMS工具箱[18]求解式(2)，得到像元x∈X的稀疏表示特征。

(3)構造隨機森林。利用像元x的稀疏表示特征和光譜信息分別構造隨機森林，即決策樹集合的構造。

3 實驗結果與分析

為了對本文算法的分類效果進行評估，對兩組高光譜遙感圖像數據集進行了實驗，為了對本文算法的分類效果進行評估，對兩組高光譜遙感圖像數據集進行了實驗；同時對于單一的光譜信息特征和單一的稀疏表示特征也采用隨進森林分類器進行分類，并將他們的分類結果與本文算法的分類結果進行了比較。實驗中采用常用的分類比較評價指標，即總精度(Overall Accuracy, OA)和Kappa系數。為了使得算法具有可比性，實驗中將各類樣本按數量隨機等分成兩部分作為訓練、測試樣本集，所有算法和實驗都按照這種方式運行 10次對結果求平均值，最優結果用粗體表示。

3.1 實驗1

實驗1使用1992年6月AVIRIS 傳感器采集的美國印第安納州 Indian Pine實驗區高光譜遙感圖像，該圖像來自Purdue 大學遙感圖像處理實驗室。去除水汽吸收和低信噪比波段后，從原始的220 個波段中選取了200個波段作為研究對象。實驗數據集使用常用的9 類典型地物作為測試樣本，共包含9345 個樣本點，如表1 所示。

3種不同方法的分類結果如表 2所示，原始Indian Pine實驗區高光譜遙感圖像及其分類結果對比如圖1所示。從表2中可以看出：(1)總精度分別由基于光譜信息方法的 87.3%，基于稀疏表示特征方法的84.8%提高到了本文方法的89.0%；(2)Kappa系數分別由基于光譜信息方法的0.851，基于稀疏表示特征方法的0.811提高到了本文方法的0.870。

表1 Indian Pine實驗區典型地物樣本信息統計表

表2 3種分類方法的實驗結果對比

3.2 實驗 2

實驗 2使用美國國家航空航天局(NASA)的機載可見/紅外成像光譜儀(AVIRIS)于1996年3月23日獲取的美國佛羅里達州 Kennedy Space Center(KSC)實驗區高光譜遙感圖像[5]。光譜范圍為 400～2500 nm，波段個數為224，去掉大氣水份吸收和低信噪比波段后，剩余176個波段作為研究對象。根據肯尼迪空間中心地面覆蓋圖和Landsat專題制圖儀(TM)影像，共得到13類典型地物樣本點5211個，如表3所示。

3種不同方法的分類結果如表4所示，原始KSC實驗區高光譜遙感圖像及其分類結果對比如圖2所示。從表4中可以看出：(1)總精度分別由基于光譜信息方法的92.0%，基于稀疏表示特征方法的91.1%提高到了本文方法的93.3%; (2)Kappa系數分別由基于光譜信息方法的0.865，基于稀疏表示特征方法的0.852提高到了本文方法的0.880。

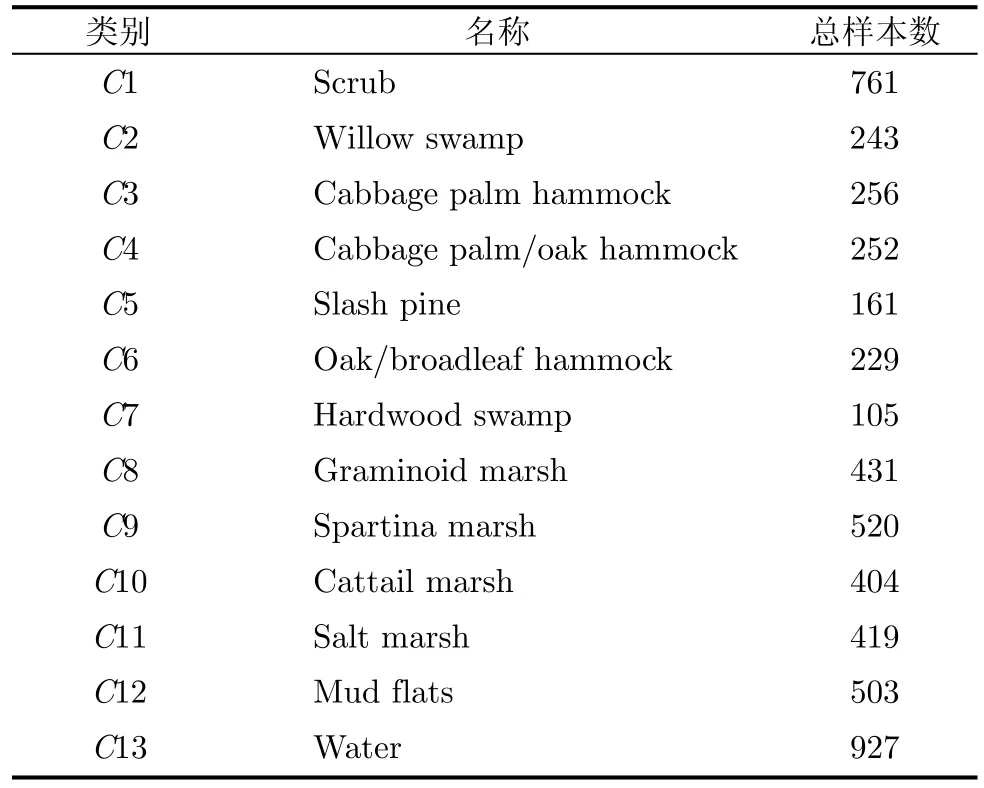
表3 KSC實驗區典型地物樣本信息統計表

圖1 Indian Pine實驗區高光譜遙感圖像分類結果對比

圖2 KSC實驗區高光譜遙感圖像分類結果對比

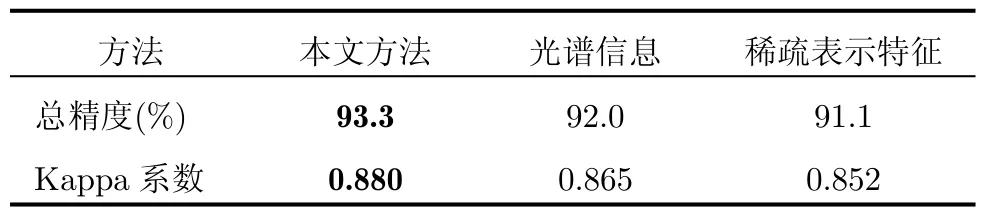
表4 3種分類方法的實驗結果對比

由于本文算法分別利用稀疏表示特征和光譜信息構造隨機森林，根據不同特征空間的分類結果進行集成得到最終結果，從上述兩個高光譜遙感圖像數據集上的實驗結果對比可以看出，本文算法在分類精度上和視覺效果上都要優于光譜信息方法和稀疏表示特征方法。另外，實驗1中光譜信息的分類結果精度高于稀疏表示特征的方法，即這兩種方法的差異性大；而實驗2中光譜信息的分類結果精度略高于稀疏表示特征的方法，即這兩種方法的差異性小，因此本文算法在實驗1上的改善程度略高于實驗 2，這與集成學習中差異性對集成結果的影響是一致的。

為了直觀比較各種分類方法花費的代價，使用運算時間作為計算復雜度的度量。實驗中使用的機器配置為雙核2.93 GHz Intel Core i3 處理器，8GB內存，在Matlab7.10環境下進行實驗。表5給出了3種方法的運行時間。由表中可以看出，本文方法的運算時間高于光譜信息方法，且略高于稀疏表示特征方法。由于本文方法的分類效果優于上述兩種方法，所以增加的計算開銷是可以接受的。

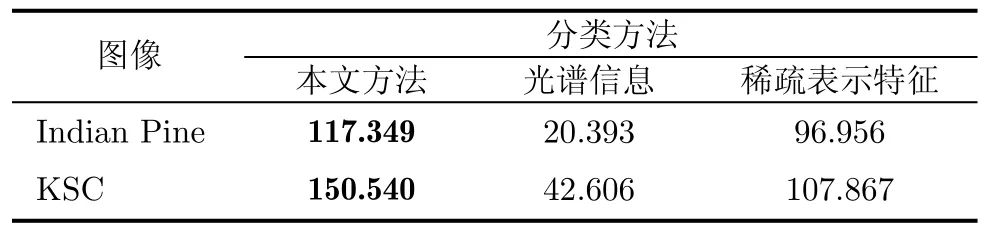
表5 3種分類方法的運行時間(s)

4 結束語

針對僅利用光譜信息導致高光譜遙感圖像分類精度較低的問題，本文提出基于稀疏表示理論提取高光譜圖像的稀疏表示特征，根據稀疏表示特征和光譜信息這兩種不同的表示形式，提出利用隨機森林方法實現圖像分類。對兩個高光譜圖像數據集分類的實驗結果表明，本文所提出的基于稀疏表示及光譜信息的高光譜圖像遙感分類算法的性能總體優于光譜信息方法和稀疏表示特征方法，在總精度和Kappa系數上相對于光譜信息方法和稀疏表示特征方法都有大幅度的提高。本文的研究工作還有許多有待改進的地方，例如，如何更加有效地融合稀疏表示特征和光譜信息，采用其它組合分類器算法獲得更佳的分類效果，進一步研究快速算法從而降低計算開銷等問題。

[1]Plaza A, Benediktsson J A, Boardman J,et al.. Recent advances in techniques for hyperspectral image processing [J].Remote Sensing of Environment, 2009, 113(9): 110-122.

[2]邸韡, 潘泉, 趙永強, 等. 高光譜圖像波段子集模糊積分融合異常檢測[J]. 電子與信息學報, 2008, 30(2): 267-271.Di Wei, Pan Quan, Zhao Yong-qiang,et al.. Anomaly target detection in hyperspectral imagery based on band subset fusion by fuzzy integral[J].Journal of Electronics&Information Technology, 2008, 30(2): 267-271.

[3]宋娟, 吳成柯, 張靜, 等. 基于分類和陪集碼的高光譜圖像無損壓縮[J]. 電子與信息學報, 2011, 33(1): 231-234.Song Juan, Wu Cheng-ke, Zhang Jing,et al.. Lossless compression of hyperspectral images based on classification and coset coding [J].Journal of Electronics&Information Technology, 2011, 33(1): 231-234.

[4]Chan J C W and Paelinckx D. Evaluation of random forest and adaboost tree-based ensemble classification and spectral band selection for ecotope mapping using airborne hyperspectral imagery[J].Remote Sensing of Environment,2008, 112(6): 2999-3011.

[5]Ham J, Chen Y, Crawford M,et al.. Investigation of the random forest framework for classification of hyperspectral data [J].IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(3): 492-501.

[6]Shahshahani B M and Landgrebe D A. The effect of unlabeled samples in reducing the small sample size problem and mitigating the hughes phenomenon[J].IEEE Transactions on Geoscience and Remote Sensing, 1994, 32(5):1087-1095.

[7]Breiman L. Random forests [J].Machine Learning, 2001,45(1): 5-32.

[8]Olshausen B A and Field D J. Emergence of simple-cell receptive field properties by learning a sparse code for natural images [J].Nature, 1996, 381(6583): 607-609.

[9]Iordache M D, Dias J M B, and Plaza A. Sparse unmixing of hyperspectral data. [J].IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(6): 2014-2039.

[10]Wright J, Ma Y, Mairal J,et al.. Sparse representations for computer vision and pattern recognition [J].Proceedings of the IEEE, 2010, 98(6): 1031-1044.

[11]余慧敏, 方廣有. 壓縮感知理論在探地雷達三維成像中的應用[J]. 電子與信息學報, 2010, 32(1): 12-16.Yu Hui-min and Fang Guang-you. Research on compressive sensing based 3D imaging method applied to ground penetrating radar [J].Journal of Electronics&Information Technology, 2010, 32(1): 12-16.

[12]屈樂樂, 方廣有, 楊天虹. 壓縮感知理論在頻率步進探地雷達偏移成像中的應用[J]. 電子與信息學報, 2011, 33(1): 21-26.Qu Le-le, Fang Guang-you, and Yang Tian-hong. The application of compressed sensing to stepped-frequency ground penetrating radar migration imaging [J].Journal of Electronics&Information Technology, 2011, 33(1): 21-26.

[13]孫玉寶, 韋志輝, 吳敏, 等. 稀疏性正則化的圖像泊松去噪算法[J]. 電子學報, 2011, 39(2): 285-290.Sun Yu-bao, Wei Zhi-hui, Wu Min,et al.. Image poisson denoising using sparse representations [J].Acta Elcetronica Sinica, 2011, 39(2): 285-290.

[14]Raina R, Battle A, Lee H,et al.. Self-taught learning: transfer learning from unlabeled data[C]. International Conference on Machine Learning, Corvallis, 2007: 759-766.

[15]Qiao Li-shan, Chen Song-can, and Tan Xiao-yang. Sparsity preserving projection with applications to face recognition [J].Pattern Recognition, 2010, 43(1): 331-341.

[16]Han Ya-hong, Wu Fei, Zhuang Yue-ting,et al.. Multi-label transfer learning with sparse representation[J].IEEE Transactions on Circuits and Systems for Video Technology,2010, 20(8): 1110-1121.

[17]Aharon M, Elad M, and Bruckstein A. K-SVD: an algorithm for designing over-complete dictionaries for sparse representation [J].IEEE Transactions on Signal Processing,2006, 54(11): 4311-4322.

[18]Mairal J, Bach F, Ponce J,et al.. Online learning for matrix factorization and sparse coding [J].Journal of Machine Learning Research, 2010, 11(1): 19-60.

[19]童慶禧, 張兵, 鄭蘭芬. 高光譜遙感: 原理、技術與應用[M].北京: 高等教育出版社, 2006: 262-272.Tong Qing-xi, Zhang Bing, and Zheng Lan-fen. Hyperspectral Remote Sensing —— Theory, Technology and Applications[M]. Beijing: Higer Education Press, 2006: 262-272.

[20]Breiman L. Bagging predictors [J].Machine Learning, 1996,24(2): 123-140.