橋補結合電路技術在力傳感器中的應用及分析

李育德，米哲敏

（1.太原理工大學 材料科學與工程學院，太原030024；2.同濟大學 電子與信息工程學院，上海201804）

在做力及重量測量時，習慣的做法是將受力傳感器的輸出信號（傳感器信號）直接傳送給測量系統的前級放大部分，傳感器與測量系統之間僅僅保持有簡單的信號傳遞關系，且傳感器只有力、電轉換作用。盡管當代儀表技術已經進入智能化時代，并且達到盡善盡美的水平，但要實現高精度測量的同時對傳感器也提出較為苛刻的要求；而要想使傳感器獲得設計水平，儀表必須提供出高質量、高穩定的使用參數與條件。之所以互相要求條件之高，其根本原因是由于傳感器與儀表二者之間不存在模擬量平衡關系。

1 橋補結合電路及構成

由電阻應變片所組成的直流惠斯頓電橋（以下簡稱電橋）就是要產生因力作用于受力模型彈性體變形而相應使橋路輸出信號，這樣就直接把測力的過程簡單地轉變為測電的過程了。被測對象的轉變必然帶來測量方法與方式的不同，其誤差表達形式及計算過程等諸多因素均會對測得結果產生影響，這是因為直接測量轉變成間接測量而造成的。橋路問題是個古老的話題，為完善這一技術手段，多年來推出了非常多的解決問題的方法、思路；得出了相應的應用條件、公式及定理，并獲得很好的效果。在當今儀器、儀表高度發達的同時有必要對橋路作更深一步的研究，以便充分地倍加掌握這一經典技術。

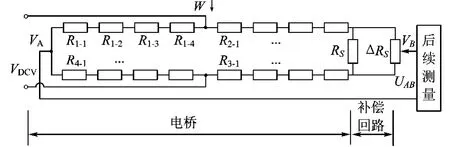
圖1 橋補結合電路

以四個傳感器組成一臺測力裝置系統為例說明。作橋補結合電路（以下簡稱橋補電路），如圖1所示。圖中：R1－1，…；R2－2，…；R3－3，…；R4－4，…代表各傳感器同一位置（名）上的應變計，RS為補償電壓的采樣電阻、RSδ為補償電阻。從圖中可以看出，橋補電路是由電橋與補償回路兩部分構成，并通過采樣電阻RS把這兩部分結合在一起的。當力W作用于傳感器后引起電橋輸出，使得后續測量電路得到一個輸入電壓信號UAB而引起數字補償系統工作，補償電阻RSδ是以數字形式對電橋輸出信號進行自動補償的（該補償是較為復雜的單元技術，為文字敘述方便，采用電位計的直觀圖形來代表該單元的轉換作用），直至達到電位VB＝VA時補償自動停止，顯示部分同步顯示出測量數值。

2 橋補電路性能分析

從圖1可以看出，構成橋補電路的前提條件就是將各傳感器的四個應變計按“同一位置”的原則串接（或并接）來組成一個橋臂，然后再把組成的四個橋臂搭成一個電橋。這樣我們可以得出圖1的簡化圖，如圖2所示的橋補電路。在這個橋補電路圖中，∑Ri｜i＝1，2，3，4表示同一位置的應變計阻值之和；∑ΔRi｜＝1，2，3，4表示同一位置的應變計阻值變量之和，用ΔRS取代補償回路RS∥RSδ，∑RL，∑RR分別表示左、右半橋應變計阻值之和；∑ΔRL，∑ΔRR分別表示左、右半橋應變計阻值變量之和。

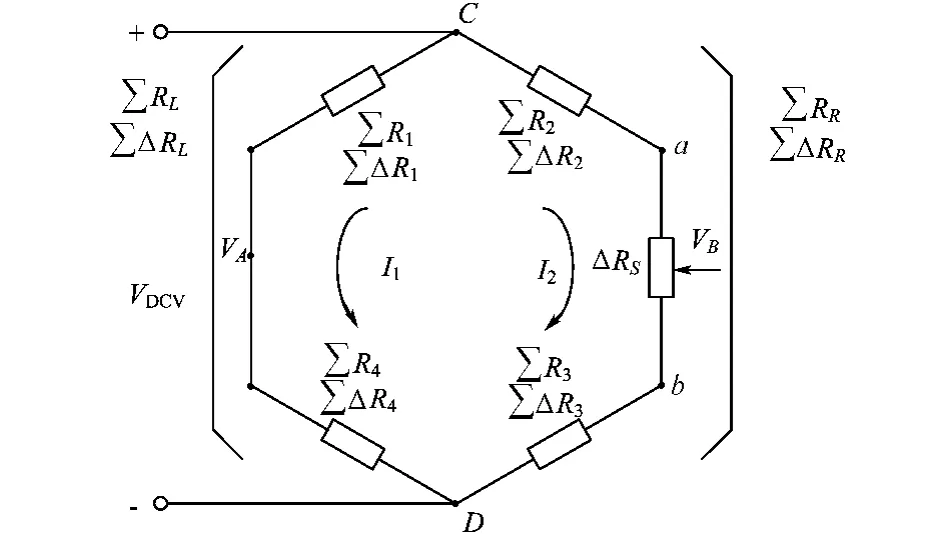
圖2 橋補電路

盡管力學模型元件可以做出許多樣式，但目前還是以通過測彎、剪、軸向以及它們的組合為主要的途徑來完成彈性元件的設計，并且本著使電橋輸出最大為目標來合理粘貼應變計的。討論電橋輸出電壓與橋路阻抗內在關系非常有必要，對了解橋補電路的實質內容很有幫助。

2.1 電橋四臂應變相等時的輸出

電橋四臂應變相等時，此時電橋習慣地稱為等臂全橋，常用的雙孔彎曲梁傳感器（S型傳感器）便是應用的實例。設有一組已按圖2所示接好的傳感器，同時做出該電路的等效電路，見圖3所示。從a，b點看，把該電路可以分成應變電路與補償電路兩部分，當電路工作時，從平衡角度理解可以產生如下等式。

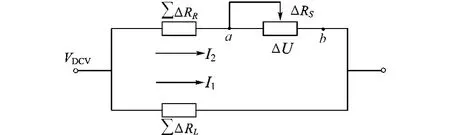
圖3 橋補等效電路

應變電壓：

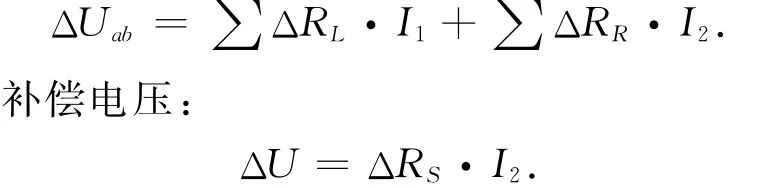
只有當ΔUab＝ΔU時可得出平衡方程，應變電壓平衡方程：

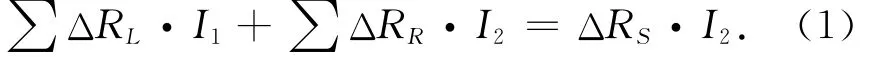
由于電橋存在著原始不平衡，使得電流表現出如下關系：

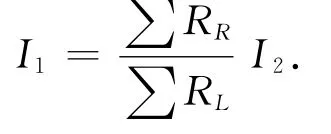
又因是等臂全橋，則有下述條件成立：

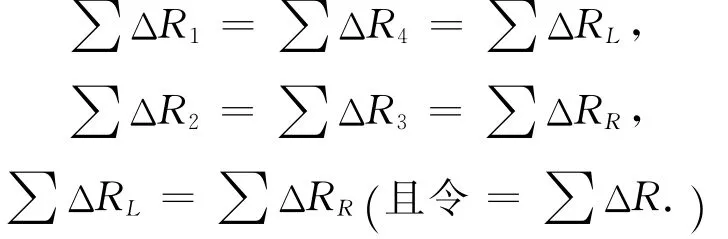
做一些代換可得以下方程。

應變電阻平衡方程：

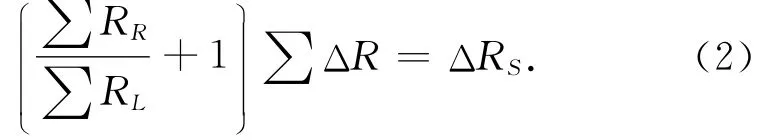
在傳感器僅重力作用時∑RR，∑RL值是不變的（應變電阻代數和為零），所以可得表達式：

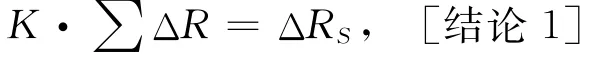
式中：常數因子

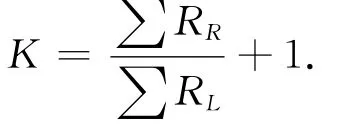
通過上述平衡方程式（1），（2）及［結論1］表達式演變可以看出，當有常數因子K存在時所做的測力或稱重的測量過程，在橋補電路里可表現為可以用ΔRS電阻的形式來補償∑ΔR的應變電阻量使得電橋恢復平衡的過程。在這種情況下，就可以把電橋的補償不再看成是電壓補償而變為電阻補償，通過電阻補償使電橋恢復平衡。通俗地講就是，因電橋阻值發生了∑ΔR量的變化使VA離開原平衡點，通過調節△RS而產生∑ΔRS的效應使VB重新與VA平衡。這樣，補償回路自然便成為電橋的一部分，這就是橋補電路不同于電橋之處，也是橋補結合電路的基本特點。

2.2 左、右半橋應變不相等時電橋的輸出

這種情況，常用的柱環式傳感器便是例子。這時，下述條件成立：

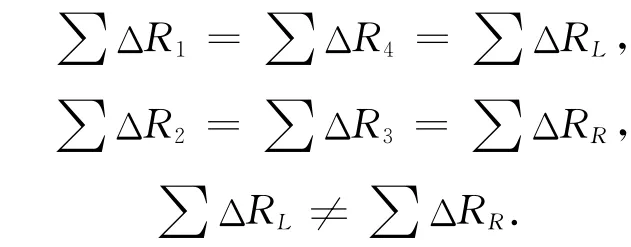
這類電橋稱為第一對稱全橋［3］。

此類型橋路的應變電阻平衡方程：

因為當有重力存在時∑RR，∑RL值不變，所以有恒等式：

但是，∑ΔRL，∑ΔRR的改變是呈線性狀態變化的，因而可以令：

式中：常數因子K＝C＋P.

比較兩個結論表達式完全相同。此時同樣可得出上述理論結果，它仍然是電阻的平衡過程。

3 同半橋中兩臂應變不相等時電橋的輸出

圓柱型、圓筒型傳感器就是屬于此類情況的典型例子。這類傳感器的應變計粘貼有豎向及橫向之別而組合成非對稱電橋。應用材料力學知識可知，在同一力的作用下豎向的應變量值將大于橫向值，也就是泊桑效應。對于制做傳感器的鋼質材料來說其相應的泊桑系數μ＝0.24～0.30范圍，在這一前提下，完全可以做到以下條件成立：

第一，橋臂應變值 ∑ΔR1，∑ΔR2，∑ΔR3，∑ΔR4都是線性變化的。

第二，同時保證實現相關關系成立，即

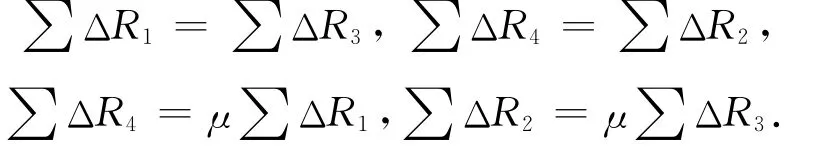
但是，正因為泊桑現象的存在，使得在傳感器受力后產生了臂阻抗變化不平衡現象。圖4是以D點為參考點比較受力前后A，B兩點阻抗變化矢量圖，從圖中看到，受力前A，B兩點同時處于某一定義平衡狀態，但在受力后則分別從原來的A，B點移至A′，B′兩點，產生了一些不平衡現象：

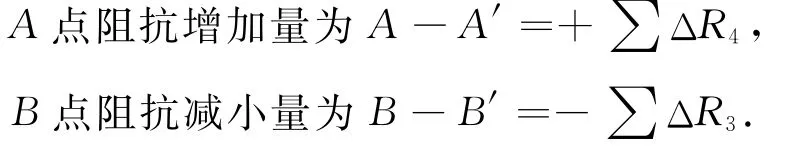
且存在著∑ΔR4＝μ｜∑ΔR3｜的關系，這樣最終導致｜B－B′｜＞｜A－A′｜的結果。

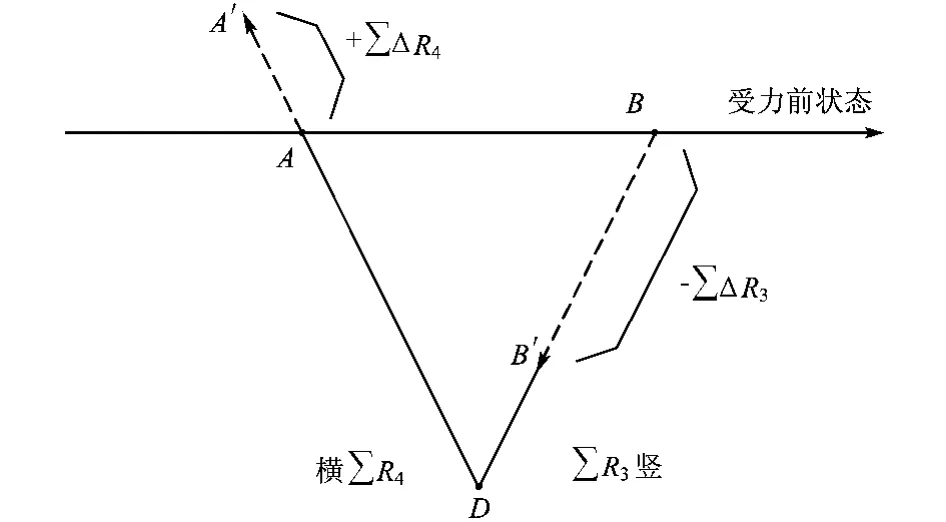
圖4 臂阻抗矢量變化

在上述2.1與2.2小節中談到僅當重力存在時∑RR，∑RL值不變，存在著一個比值常數。但在該例子中∑ΔRL，∑ΔRR值因受到∑ΔR4＝μ∑ΔR1，∑ΔR2＝μ∑ΔR3關系的影響而不在保持恒定，這樣是否導致∑RR／∑RL比值也會受到同樣的影響而不表現不變性。

設，在傳感器受力前比值為：

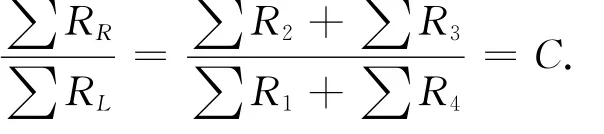
在傳感器受力后左、右半橋阻抗為：

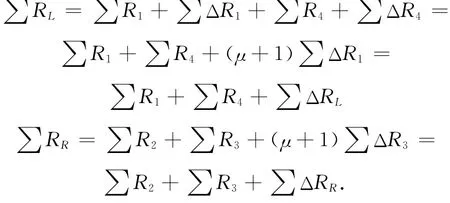
其比值為：

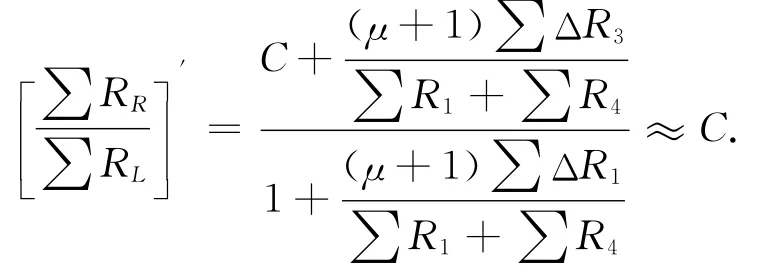
這樣可以認為 ∑RR／∑RL比值受重力的影響可忽略不計。

該類型橋路的應變電阻平衡方程：

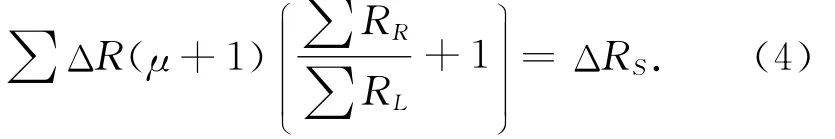
因對某一個傳感器來說μ值是恒定的，這樣可得表達式：

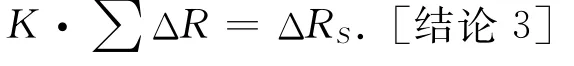
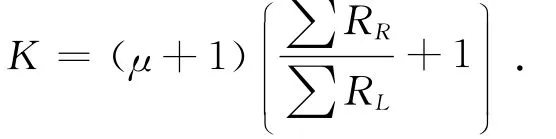
式中：常數因子同樣可得出上述的理論結果，稱重和測力過程仍然是電阻的線性補償和橋路電阻的線性平衡過程。

4 結論

電阻應變式測試技術中等臂全橋、對稱全橋以及非對稱全橋是常用的電橋電路，針對這三種電路使用的廣泛性及覆蓋性的特點，分別逐一地論證實現橋補結合電路的可能性（上述三個結論的導出充分表明了可能性）。這樣就可以實現在電阻應變式測試系統中，僅對電源提出能保證測量的靈敏度就行了的唯一要求。這也是橋補結合電路的特點之一。

橋補結合電路技術的的成功實現后，完全可以克服傳統的惠斯頓電橋所表現出難以彌補的一些不足之處，并對測試技術帶來了某些改進。

［1］ 秦曾煌.電工學［M］.北京：高等教育出版社，1999.

［2］ 康華光.電子技術基礎［M］.北京：人民教育出版社，1982.

［3］ 王化祥，張淑英.傳感器原理及應用［M］.天津：天津大學出版社，1990.

［4］ 袁希光.傳感器技術手冊［M］.北京：國防工業出版社，1986.

［5］ 機械工業部儀器儀表工業局.非電量電測變換技術［M］.北京：機械工業出版社，1988.