井用泵水力模型設計及試驗研究

趙秋霞

（太原理工大學 力學學院，太原030024）

離心泵是量大面廣的通用機械，在國民經濟各部門發揮著重要作用。為了設計高效節能的離心泵，國內外專家學者進行了大量探索研究，但至今仍沒有成熟的理論和設計方法，水泵的水力模型設計依然是采用相似設計原理并在大量統計資料基礎上建立的經驗公式和速度系數法，泵性能的好壞也無法通過理論計算得出，只能通過實驗驗證。井用泵屬離心泵范疇，但井用泵機組最大外徑受到井徑限制，所以水力模型設計不能完全套用離心泵設計方法，有其獨特性。因此我們針對井用泵特點采取了理論設計和實驗相結合的方法，進行了大量設計研究、實驗分析，提出了井用泵水力模型主要幾何參數的選取原則和選擇范圍。并完成了適用多種井徑、多種型號的井用泵水力模型設計和樣機試制工作。

1 葉輪進口參數選取與實驗分析

1.1 葉輪軸面投影圖

井用泵的核心工作部件是葉輪，葉輪的幾何形狀是由軸面投影圖和平面投影圖共同表示的。在初步確定葉輪幾何參數后，首先要繪制軸面投影圖，然后再用保角變換法或扭曲三角形法繪制平面投影圖。軸面投影圖繪制往往是依靠經驗繪制的，有很大的任意性，我們采取了與傳統離心泵不同的方法，將葉輪后蓋板設計成傾斜的，接近混流泵形狀，目的是加大葉輪做功能力并使之與導流殼合理匹配。如200QJ32泵葉輪軸面投影圖采用了兩種方案，一種后蓋板傾斜度較大，（取θ＝25°），另一種較小（取θ＝13°）。試驗表明第一種方案效果較好。圖1為兩種葉輪軸面投影圖比較。

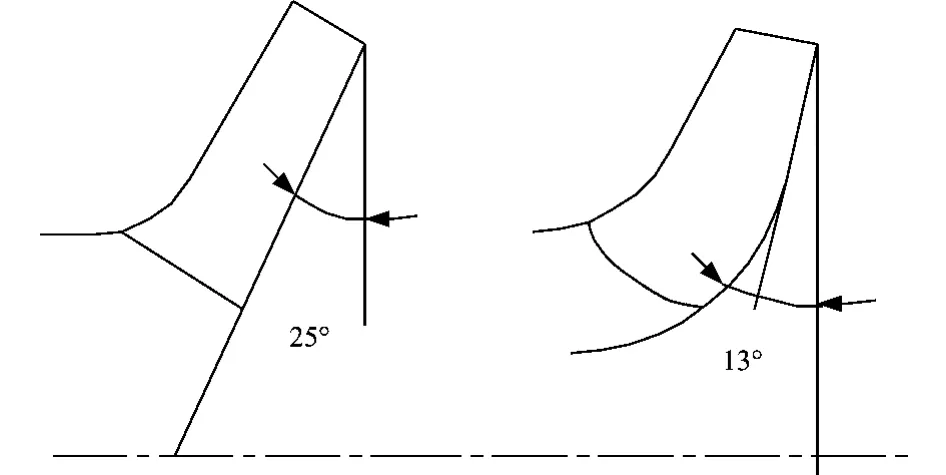
圖1 兩種葉輪軸面投影圖

1.2 葉輪進口直徑D0

井用泵因潛入水中工作，故沒有吸程，不受汽蝕性能影響，因此可適當縮小葉輪進口直徑，提高進口處液流速度，使密封環處泄漏量減小，容積效率提高。

以200QJ32葉輪為例，葉輪進口當量直徑

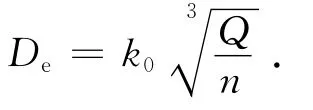
式中：k0為葉輪入口系數；Q為體積流量；n為泵轉速。實驗中采用了兩種方案。

第 一種方案：取K0＝4.015，Q＝32m3／h，n＝2 850r／min.經計算得De＝58.7mm，取輪轂直徑dh＝28mm，經計算得葉輪進口直徑＝65mm，經實驗，設計點水泵效率η＝71.6%，高效點位于Q＝42m3／h處。

第二種方案：取K0＝3.63，Q和h同上，經計算得De＝53mm.取輪轂直徑dh＝28mm，得D0＝60 mm，經實驗，設計點水泵效率η＝73.2%，高效點位于Q＝37m3／h處。

對兩種方案比較，選用第二種方案更為合理。

1.3 葉片進口邊位置

葉片進口邊位置適當向吸入口方向延伸，可以增加葉片表面積，減少單位面積負荷，使液體提早接受葉片作用。葉片進口邊是按無旋流動設計的，即絕對速度的圓周分速度vu1＝0，葉片進口邊向吸入口延伸時，圓周速度v01和相對速度vw1均減小，見圖2，這樣可以減小沖擊損失，改善泵進口流動狀態。延伸程度以不堵塞葉輪進口為宜。試驗中200QJ20泵采取了兩種方案，一組葉輪進口邊延伸，一組進口邊去掉4mm.實驗結果為，第二組設計點揚程下降了4m，效率下降2%。試驗曲線見圖3。

圖2 葉片進口邊延伸前后速度三角形

圖中v1為葉片進口絕對速度；vm1為葉片進口絕對速度的軸面分速度；v01為葉片進口圓周速度（延伸前）；vw1為葉片進口相對速度（延伸前）；v′01為葉片進口圓周速度（延伸后）；v′w1為葉片進口相對速度（延伸后）。

圖3 葉片延伸前后Q—η曲線

1.4 葉片進口安裝角

1.5 葉片進口邊形狀

葉片進口邊均采用扭曲葉片形狀。由于采用一維設計理論，假設軸面速度vm1是均勻分布的，但進口邊各點v01不同，β1不同。為符合這種流動狀況，需采用扭曲葉片，增加過流斷面面積。

2 葉片出口參數選取與實驗分析

2.1 葉片出口外徑D2和葉片出口邊寬度b2

對于一定性能的泵，主要是確定其出口參數（D2，b2，β2）和出口速度三角形。根據速度系數法，葉片出口直徑和出口寬度為：

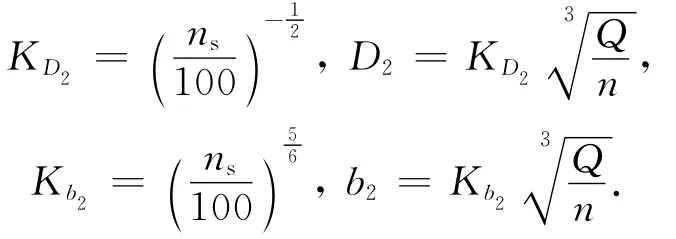
式中：ns為比轉數；KD2為出口外徑速度系數；Kb2為出口寬度速度系數［1－2］。

設計時依據上述經驗公式，初步確定中間流線葉片出口直徑和出口寬度，然后依據繪出的葉輪軸面投影圖以及葉輪和導流殼匹配情況確定前后蓋板流線葉片出口直徑，最后根據實驗結果最終確定各條流線出口直徑D2。

井用泵壓水室一般采用導流殼（空間導葉）結構，這樣在葉輪和導流殼之間形成一個環形空間，當液流流出葉輪后突然擴散，流動方向改變，在導流殼入口處產生旋渦和沖擊損失，使得泵揚程和效率下降，所以井泵效率低于蝸殼式和徑向導葉式離心泵效率。為解決這一問題，往往采用加大葉片出口寬度b2的方法，提高泵揚程并使高效點適當向大流量偏移。實驗結果表示，這一方法對于中低比轉數可行，當設計點比轉數ns＝100～200時，b2可增加5%～20%。如200QJ 20型泵，比轉數ns＝103，計算出的b2＝8.13mm，最初設計時取b2＝11.5mm，比計算值增加了41%，結果高效點偏移至35m3／h處，設計點效率僅為62%，修改設計后，取b2＝9 mm，比計算值增加10.7%.實驗結果為，設計點效率提高至67.7%，且高效點偏移不多，試驗曲線如圖4所示。

圖4 不同b2時的Q—η曲線

2.2 葉片出口安裝角β ［5－6］2a

由歐拉葉片式泵的基本方程，當葉輪進口無旋時（vu1＝0），無窮多葉片理論揚程為

式中：QT為理論流量；v02為葉片出口圓周速度；vu2∞為無窮多葉片出口絕對速度的圓周分速度；vm2∞為無窮多葉片出口絕對速度的軸面分速度，v02∞為無窮多葉片出口絕對速度；β2a為無窮多葉片出口安裝角。無窮多葉片出口速度三角形如圖5所示。

圖5 無窮多葉片出口速度三角形

由速度三角形可知，當轉速n和出口D2、b2一定時，vm2∞不變，當β2a增大時，可使vu2∞增大，HT∞增大，因此為了提高泵的揚程，希望β2a取得大些。但β2a越大，泵性能曲線 （Q－H 曲線）變平坦，甚至會產生駝峰，造成泵工作出現不穩定情況。另一方面，從能量角度分析，泵理論揚程可分為靜揚程HST∞和動揚程Hd∞兩部分，而靜揚程與理論揚程之比稱為反作用度τ［3］：

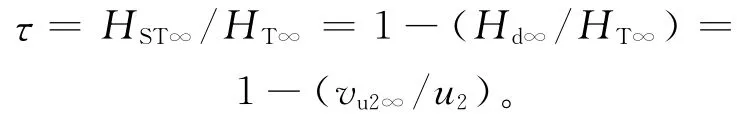
當β2a增大時，τ減小，Hd∞增加，葉輪出口處絕對速度大，使得導流殼中水力損失增加，所以希望β2a取得小些。綜上所述，應根據不同的比轉數，選取一個合理的β2a值。但實際上葉片都是有限的，葉片實際出口安裝角β2小于β2a，井泵中一般取β2為（22°～35°），小比轉數取大值。如200QJ20泵，從最初的β2＝28°，包角φ＝95°，修改為β2＝35°，φ＝90°。由于縮短了葉片長度，流道變得光滑流暢了，在其它參數不變的情況下，揚程和泵效率均有所提高。

3 導流殼參數選取與實驗分析

導流殼是壓水室的一種形式，又稱空間導葉，是一個重要的轉換能量裝置。有資料表明壓水室中的水力損失占泵內水力損失的40%～50%，因此設計一個好的葉輪很重要，但同時不容忽視導流殼設計。

3.1 葉輪和導流殼的合理匹配

為使葉輪和導流殼很好配合，應將二者作為一個整體來設計，即在確定葉輪軸面投影圖的同時確定導流殼軸面投影圖，導流殼葉片進口邊尺寸與葉輪葉片出口邊尺寸相匹配，導流殼葉片出口邊尺寸與葉輪葉片進口邊尺寸相匹配，并保證其軸面面積變化均勻，見圖6。由于葉輪后蓋板傾斜，前后蓋板流線相差較多，因此必須斜切葉輪出口外徑，否則會造成二次回流，增大水力損失。斜切角度會使泵特性曲線（Q-H曲線）產生變化，特別是對關死點揚程影響較大，斜切角度一般由試驗確定，并與導流殼相互配合。

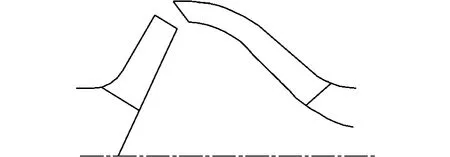
圖6 葉輪與導流殼相互配合

3.2 導流殼喉部面積

導流殼葉片進口處面積稱為喉部面積，是一個關鍵尺寸，對泵特性曲線形狀和高效點位置影響很大。通過實驗證明，當比轉數ns＝100～250時，喉部面積S3與葉輪出口面積S2之比取1～0.7為宜，喉部斷面形狀為正方形時，水力半徑最大，效果最好，但由于結構及空間尺寸限制，一般無法成正方形，所以要盡量接近矩形。如200QJ32型泵導流殼，最初設計時S3／S2＝1.10，結果高效點過多偏向大流量，后修改設計，使S3／S2＝0.90，結果設計點效率提高了2%，且高效點接近設計點。盡管目前人們為了提高產品通用化，希望采用一種導流殼配合多種葉輪，但從性能角度說，是不合理的。

3.3 導流殼葉片進出口安裝角

3.3.1 導流殼葉片進口安裝角α3

導流殼葉片進出口液流角為α′3＝vm3／vu3，再加上一個正沖角Δα3即為葉片進口安裝角α3。式中vm3為導流殼葉片進口邊計算點軸面速度，與流量有關，vu3為進口邊計算點圓周分速度，與葉輪葉片出口速度矩有關。當ns＝100～250，一般取α3＝15°～30°，ns大的水泵取大值。

3.3.2 導流殼葉片出口安裝角α4

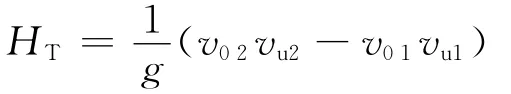
由歐拉葉片式泵基本方程可知，要想提高有限葉片的理論揚程HT，就應使vu1＝0，導流殼的一個重要作用就是消除預旋，所以取α4接近90°。式中HT為有限葉片理論揚程，vu2為有限葉片絕對速度的圓周分速度；vm2為有限葉片絕對速度的軸面分速度。

4 結論

本次設計的井用泵水力模型，是基于一維理論，根據相似理論總結出的速度系數法進行的，過流部件各參數均為比轉數ns的函數，且有較大的選擇范圍，但各參數之間又是相互依存、相互制約的，必須綜合考慮。依據上述原則設計的多種型號井用泵水力模型各項性能指標均達到和超過國家標準要求，科研成果完全轉化為社會生產力，產品批量投入市場。今后應不斷探索水泵設計的新理論、新方法，密切關注水泵研究新進展。

［1］ 關醒凡.泵的理論與設計［M］.北京：機械工業出版社，1987：185-240.

［2］ 辛東旭.泵設計生產新工藝新技術與質量驗收標準規范實務全書（第二卷）［M］.北京：北方工業出版社，2006：423-465.

［3］ 郭麗君，何川主編.泵與風機（第三版）［M］.北京：中國電力出版社，2004：20-28.

［4］ 陳允中，曹占友，鄧國強，黃紅梅等.泵手冊（第三版）［M］.北京：中國石化出版社，2002：268-330.

［5］ 關醒凡.現代泵技術手冊［M］.北京：宇航出版社，1995：80-90.

［6］ 張景松.流體力學與流體機械［M］.徐州：中國礦業大學出版社，2009：10-46.