黃河大堤邊坡穩定的強度折減法分析
姜 波
(新疆水利水電科學研究院,新疆烏魯木齊 830049)
0 引言
黃河下游共有各類堤防約2290 km,是防御洪水的主要屏障。2004年國家投入巨額資金開始在黃河兩岸修筑標準化堤防,目前下游南岸堤防已投入使用。標準化堤防是集“防洪保障線、搶險交通線和生態景觀線”于一體的國家重點工程項目,承擔著保證黃河安瀾、保護沿黃河兩岸人民生命財產安全的重要作用。因此,黃河大堤的安全、邊坡的穩定具有重要意義。隨著近些年來計算機科學的大力發展,有限元方法在計算邊坡穩定的問題中得到了越來越多的應用。
與傳統的方法相比較而言,這種方法可以考慮較復雜的模型邊界條件和材料的不均勻性,在計算邊坡穩定問題時,可以模擬滑坡土體可能的運動方向,不需要假定滑裂面的位置,而且該方法考慮了土體的本構關系。
有限元強度折減法與Bishop邊坡穩定計算方法中安全系數的定義[1]相結合,將土體的強度參數除以一定的系數后進行計算,等到所除的系數正好使土體達到臨界破壞時,此時的系數即為安全系數[2]。本文將以這種方法為依據進行分析。
1 強度折減法的基本原理
強度折減法的基本原理是將土體的強度參數除以一個系數后進行有限元計算,其表達式為:

式中:c0,φ0,Ψ0——土體的強度參數;
c',φ',Ψ'——折減后的強度參數;
Fs——計算所求的安全系數,它擁有與極限平衡方法相同概念的強度儲備含義[3]。
在計算中,使用場的作用帶動土體強度參數的折減,即令粘聚力等于場θ的函數c(θ),令摩擦角等于φ(θ)。在計算過程中,強度參數由1倍的值開始折減,最終折減至0.1倍的值,因為折減至0會導致數值奇異。
因此得到以下關系式:
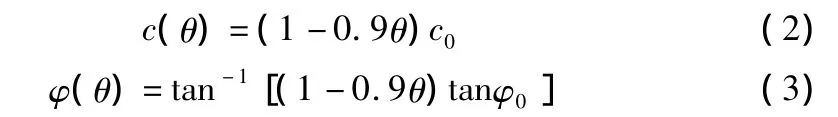
由以上各式得出安全系數的表達式為:

2 極限狀態的判別
本文采用Mohr-Coulomb屈服準則。至于土體極限狀態的判別,學術界有計算終止[2]、位移突變[4]、塑性區貫通[5]三種主要方法。本文計算中采用文獻[4]的方法,用邊坡某點位移的突變作為判別依據。
3 計算分析
3.1 臨河堤坡未迎水時的穩定分析
黃河大堤標準化堤防的典型斷面如圖1所示[6]。大堤高8 m;堤頂寬10 m;上下游堤坡均為1∶3;淤背區高4 m,寬100 m。計算斷面的截取范圍是:河床20 m;淤背區20 m;堤基8 m,計算網格如圖2所示。堤坡未迎水時的強度參數是:彈性模量100 MPa,泊松比 0.3,重度 20.4 kN/m3,粘聚力 10 kPa,摩擦角 20°。計算模型底部用固定約束,兩邊用水平方向的約束。施加荷載的時候,先加載重力,再進行參數的折減。
計算結束以后,取堤頂臨河有限元節點做的觀察點,畫出它的位移和場的關系圖,見圖3。
從圖3中的曲線中選取突變時的場值來計算安全系數,突變時 θ=0.545,代到式(4)中,則得到安全系數為 Fs=1.963。由于Fs=1.963>1,所以臨河堤坡未迎水時是安全穩定的。大堤失穩時的變形網格圖、位移矢量圖見圖4,圖5。
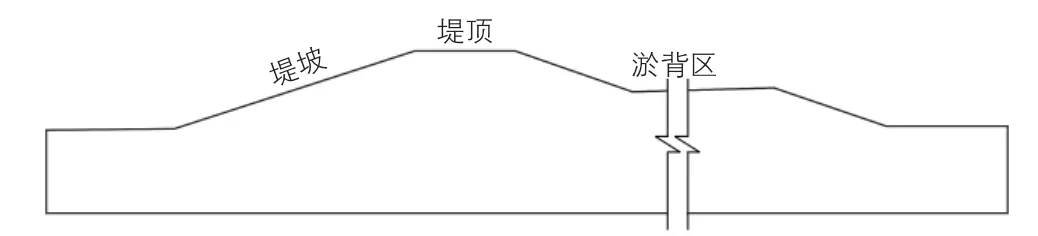
圖1 黃河大堤標準化堤防典型斷面

圖2 計算網格圖
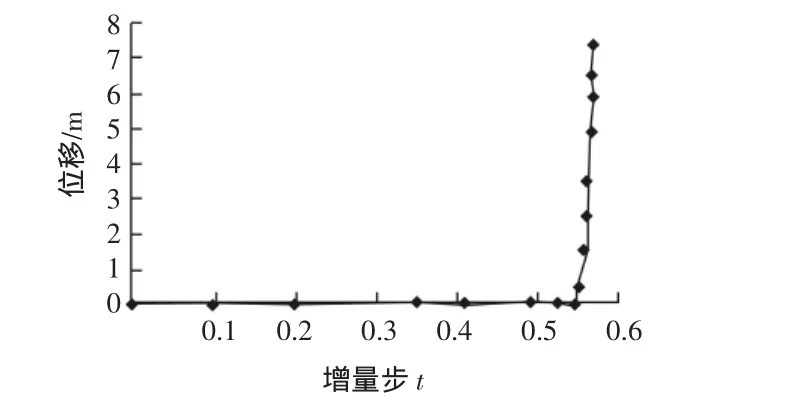
圖3 堤坡未迎水時觀察點位移與場的關系
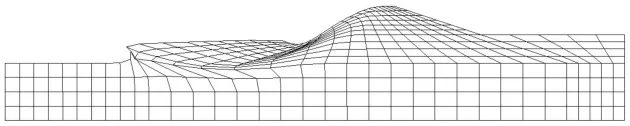
圖4 失穩時變形網格圖
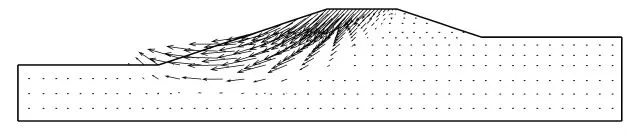
圖5 失穩時位移矢量圖
3.2 河床水位達到堤頂時的穩定分析
由于土體材料的強度參數粘聚力c和內摩擦角φ會隨著含水量的增加而逐漸減小[7],因此有必要對黃河大堤迎水時的堤坡穩定進行分析。
本文選取河床水位達到堤頂時的最不利工況進行計算分析。大堤土體受到水的浸潤作用后材料參數改變為:彈性模量100 MPa,泊松比 0.3,重度 12.24 kN/m3,粘聚力 6 kPa,摩擦角12°。邊界條件與荷載情況保持不變。
計算結束后,選擇同一個觀察點,位移與場的關系曲線如圖6所示。
圖6中的突變點為 θ=0.315,代入到式(4)中,則 Fs=1.395。由于河床水位達到堤頂時的安全系數Fs=1.395>1,所以堤坡仍然是安全穩定的。
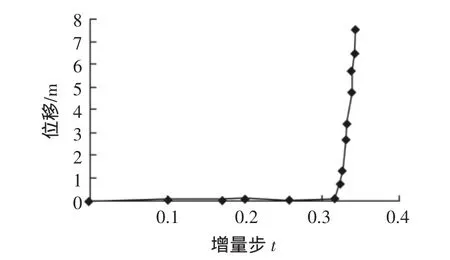
圖6 河床水位達到堤頂時固定測點位移與增量步的關系
4 結語
本文用有限元方法計算了黃河大堤的邊坡穩定問題,得出的結論主要有以下兩點:
1)黃河大堤在臨河堤坡未迎水的工況下,邊坡穩定安全系數為Fs=1.963>1,堤坡是安全穩定的。
2)河床水位達到堤頂時的最不利工況下,由于土體材料的強度隨著含水量的增加而減小,使得邊坡穩定安全系數減小為Fs=1.395>1,但堤坡仍然是安全穩定的。因此證明黃河大堤的邊坡是安全可靠的。本文也證明了用有限元強度折減法計算河道堤防邊坡穩定問題的可行性,為相關類似工程的分析提供了參考和借鑒。
[1]Bishop A W.The use of the slip circle in stability analysis of slope[J].Geotechnique,1955,5(1):7-17.
[2]鄭穎人,趙尚毅.巖土工程極限分析有限元法及其應用[J].土木工程學報,2005,38(1):91-98.
[3]曹先鋒,徐千軍.邊坡穩定分析的溫控參數折減有限元[J].巖土工程學報,2006,11(28):2039-2042.
[4]Griffiths D V,Lane,P.A.Slope stability analysis by finite elements[J].Geotechnique,1999,49(3):387-403.
[5]欒茂田,武亞軍,年廷凱.強度折減有限元法中邊坡失穩的塑性區判據及其應用[J].防災減災工程學報,2003,23(3):1-8.
[6]河南河務局.河南黃河志[M].鄭州:黃河水利出版社,2009.
[7]黨 靖,胡李俐,南 帥.含水量及天然密度對土體抗剪強度參數的影響研究[J].中國西部科技,2007(5):14-15.
[8]張肆紅,路曉光.強度折減法在邊坡穩定性分析中的運用[J].山西建筑,2010,36(6):92-93.

