MicroRNA-24 對心肌梗死后心肌細胞凋亡的調(diào)控作用*
王 玨, 黃偉聰, 鄭亮承, 孫成超, 鄭 哲
(1溫州醫(yī)學院附屬第一醫(yī)院心胸外科,浙江 溫州325000;2阜外心血管病醫(yī)院外科,北京100037)
心肌梗死是危害人類健康、造成心源性死亡的主要因素之一,心肌梗死過程中心肌細胞缺血缺氧會造成細胞不可逆轉(zhuǎn)的死亡或凋亡,進而引起心功能不全[1]。心肌細胞凋亡在心梗后心臟重塑及心力衰竭的病理生理過程中扮演了重要角色,減少心肌細胞凋亡能改善心梗后心功能,改善心臟重塑過程[2]。MicroRNA(miRNA)在機體內(nèi)主要通過抑制mRNA 轉(zhuǎn)錄或促mRNA 降解來行使負向調(diào)控基因表達的功能,參與機體各種疾病的發(fā)生發(fā)展過程[3]。研究發(fā)現(xiàn)在心臟中miRNA 能夠調(diào)控各種心臟疾病的病理生理過程[4]。MicroRNA-24(miR-24)是一種心臟富集的miRNA,有報道顯示抑制miR-24 能夠誘導視網(wǎng)膜細胞的凋亡水平[5],然而相關(guān)于miR-24 在心梗后的變化及其作用機制國內(nèi)外鮮有報道。本研究旨在觀察miR-24 對于缺血缺氧條件下心肌細胞凋亡水平的調(diào)節(jié),探討miR-24 對心肌梗死后心功能及心肌細胞凋亡水平的影響。
材 料 和 方 法
1 材料
1.1 動物 本實驗所使用的實驗動物為12 周齡,25 ~30 g 的C57BL/6 雄性小鼠用于心肌梗死模型的制作;出生后1 ~3 d SPF 級Sprague-Dawley(SD)大鼠乳鼠用于獲得原代心肌細胞。實驗動物均購自北京大學醫(yī)學部實驗動物中心。所有動物實驗均得到北京協(xié)和醫(yī)學院阜外心血管病醫(yī)院動物委員會的批準,所有操作均按照《北京實驗動物管理條理(1996)》的相關(guān)規(guī)定進行。
1.2 主要試劑和儀器 細胞轉(zhuǎn)染的miRNA 前體Pre-miRTMmiR-24 Precursor 或抑制劑Anti-miRTMmiR-24 Inhibitors,及轉(zhuǎn)染試劑脂質(zhì)體siPORT NeoFX Transfection Agent 均由ABI 合成;組織轉(zhuǎn)染miRNA慢病毒由上海吉凱生物有限公司合成;qRT-PCR 試劑Power SYBR green PCR master mix、TaqMan Universal PCR Mix、TaqMan microRNA Assay 均購自ABI;MMLV 逆轉(zhuǎn)錄酶、Caspase-Glo? 3/7 Assay 購自Promega,TUNEL 染色試劑盒(Roche),Genbox 厭氧產(chǎn)氣包(Biomerieux),DAPI 細胞核染液(碧云天生物技術(shù)研究所);小動物超聲心動圖儀(Visualsonics),12 MHz 頻率超聲探頭(Philips);小動物呼吸機(Harvard Apparatus);倒置相差/熒光顯微鏡(Olympus);ABI-7300 熒光實時定量PCR 儀(ABI);CO2恒溫細胞培養(yǎng)箱(Napco 5410-220)。
2 方法
2. 1 小鼠心肌梗死模型的制備及轉(zhuǎn)染 雄性C57BL/6 小鼠25 ~30 g 用2%水合氯醛(100 mg/kg)腹腔注射麻醉。直視下氣管切開,小動物呼吸機輔助呼吸,潮氣量7 ~8 mL,呼吸頻率每分鐘120 次,呼吸比1∶2。左第4 肋間入胸,識別前降支走行范圍,7/0 滑線結(jié)扎前降支,當左心室前壁部分顏色轉(zhuǎn)為蒼白且出現(xiàn)心電圖示波為心肌梗死表現(xiàn)時確認本模型制作成功。轉(zhuǎn)染用慢病毒由上海吉凱生物有限公司合成,慢病毒構(gòu)建方法參見參考文獻[6],小鼠心梗模型隨機分為假手術(shù)組、空載體組(攜帶GFP 的慢病毒空載體以4 ×107TU 的病毒數(shù)進行心肌組織局部注射轉(zhuǎn)染,n=53)、miR-24 轉(zhuǎn)染組(攜帶miR-24 的慢病毒,以4 ×107TU 的病毒數(shù)進行心肌組織局部注射,n=35)及單純心肌梗死組(n=21)。
2.2 小動物心臟超聲心動圖檢測 心梗后2 周,異氟醚吸入麻醉動物,取仰臥位。使用Vevo 770 High-Resolution Imaging System 超聲儀,探頭頻率為RMV 704(40 MHz )。取左室乳頭肌水平二維左室短軸切面,記錄左室收縮期末徑及左室舒張期末徑,由超聲心動圖電腦自動計算左室射血分數(shù)(left ventricular ejection fraction,LVEF)和左室短軸縮短率(left ventricular fractional shortening,LVFS),取連續(xù)3 個心動周期的平均值。
2.3 乳鼠心肌細胞的轉(zhuǎn)染及缺血缺氧模型 取新生1 ~3 d SD 大鼠乳鼠,無菌條件下剔出心臟,去除心房、大血管等結(jié)締組織,加入配置的胰酶心肌細胞消化液進行消化;收集組織消化懸液離心,棄上清,用含10%FBS 的DMEM 培養(yǎng)液重懸細胞,進行心肌細胞培養(yǎng),詳細方法參見參考文獻[7]。按5 ×104/cm2的密度接種至細胞培養(yǎng)瓶或培養(yǎng)板。用siPORT轉(zhuǎn)染miRNA 到心肌細胞,轉(zhuǎn)染后12 h 進行缺血缺氧處理[7],轉(zhuǎn)染方法按照ABI 公司實驗操作流程進行,轉(zhuǎn)染終濃度為30 μmol/L。心肌細胞缺血缺氧方法,將心肌細胞培養(yǎng)液置換為無血清DMEM 培養(yǎng)基,并將培養(yǎng)皿放于缺氧罐內(nèi),在缺氧罐中放置Genbox 厭氧產(chǎn)氣包,制造缺血缺氧模型,最后將缺氧罐放置于37 ℃5% CO2培養(yǎng)箱中進行培養(yǎng),缺血缺氧后48 h收集細胞進行下一步的實驗。miRNA 轉(zhuǎn)染心臟心肌細胞功能研究實驗分組:正常未處理組(培養(yǎng)條件同處理組)、miRNA 轉(zhuǎn)染對照組(30 μmol/L)和miR-24前體或抑制劑轉(zhuǎn)染組(30 μmol/L)。
3 實驗指標的檢測
3.1 心肌組織Masson 染色病理學檢測 石蠟切片常規(guī)脫蠟入水,雙蒸水洗。蒸餾水沖洗干凈入Ⅰ液染2 min;再次蒸餾水流水沖洗干凈,入II 液染15 min;液染5 min(苯胺藍2.5 g,冰乙酸2 mL,蒸餾水100 mL)。1%冰乙酸溶液浸洗5 min。梯度乙醇脫水,入二甲苯,中性樹脂封片。
3.2 心肌細胞caspase-3/7 活性測定 培養(yǎng)的心肌細胞約為4 ×107/L,96 孔板,待測各孔添加100 μL細胞懸液。將caspase-Glo 試劑按照1∶1 原則加入各孔中。300 ~500 r/min 的轉(zhuǎn)速輕柔混勻30 秒,室溫(18 ~22 ℃)孵育2 h。孵育后的樣品板放入VeritasTM發(fā)光檢測儀中,檢測每個樣品的熒光值,進行數(shù)據(jù)分析。
3.3 TUNEL 染色石蠟包埋組織切片檢測 常規(guī)脫蠟處理組織切片,梯度乙醇浸洗,滴加蛋白酶K 溶液,室溫孵育。滴加100 μL 1 ×TdT 平衡緩沖液,室溫孵育10 ~30 min。在每個樣本上滴加60 μL TdT標記反應(yīng)混合物。封口膜覆蓋樣本。于37 ℃孵育60 ~90 min。465 ~495 nm 波長綠色熒光激發(fā)并對被標記的凋亡細胞進行分析。
3.4 實時定量PCR miRNA 檢測 以心肌梗死邊帶為標志,區(qū)分心梗區(qū)、心梗周邊區(qū)及遠心梗區(qū)[8],抽提組織RNA 后,利用TaqMan MicroRNA Assay Kit 中的特異性莖環(huán)逆轉(zhuǎn)錄引物和TaqMan MicroRNA Reverse Transcript Kit 對單種類型的miRNA 進行特異性的逆轉(zhuǎn)錄反應(yīng),合成相應(yīng)的miRNA-莖環(huán)引物cDNA。利用TaqMan MicroRNA Assay Kit 中的TaqMan探針和miRNA 特異引物進行實時熒光定量PCR 反應(yīng)(TaqMan qPCR),檢測miRNA 表達水平。以U6 snRNA 為內(nèi)參,反應(yīng)體系為20 μL,2-ΔΔCt方法計算目標miRNA 的相對表達水平。定量反應(yīng)條件為95 ℃10 min,擴增1 個循環(huán),95 ℃15 s,擴增40 個循環(huán),62℃1 min 擴增40 個循環(huán),在每個循環(huán)的62 ℃時測定熒光。
3.5 表達譜芯片檢測 心肌細胞轉(zhuǎn)染miR-24 后表達譜芯片檢測由北京博奧生物有限公司完成,使用Affymetrix 生物芯片檢測技術(shù),分別對miR-24 過表達轉(zhuǎn)染組及對照組進行檢測,每組進行2 次實驗,具體方法按照CapitalBio 公司實驗操作流程進行。差異表達基因符合以下標準:(1)符合表達基因的判定標準;(2)兩組間基因點信號比值>1.5 或<0.5。獲得表達譜芯片結(jié)果后,刪除熒光信號弱的基因及沒有基因名稱的基因,以1.5 倍標準篩選基因,以TargetScan 6.2 網(wǎng)絡(luò)數(shù)據(jù)庫為參照進行生物信息學分析(http://www. targetscan. org/),獲得miR-24 的可能作用靶點。
4 統(tǒng)計學處理
用SPSS 13.0 統(tǒng)計軟件進行分析。數(shù)據(jù)以均數(shù)±標準差(mean ±SD)表示,多組間比較采用單因素方差分析(ANOVA),組間兩兩比較采用最小顯著差異法(LSD 法),以P <0.05 為差異有統(tǒng)計學意義。
結(jié) 果
1 心梗組織中miR-24 表達水平的變化
qRT-PCR 檢測發(fā)現(xiàn),相對于假手術(shù)組,心肌梗死區(qū)及心肌梗死周邊區(qū)的miR-24 表達量明顯下調(diào),這種下調(diào)在1 周左右達高峰(P <0.01),在2 周時與假手術(shù)組比較仍有顯著差異(P <0.01),在4 周左右恢復(fù)到假手術(shù)組水平,見圖1。
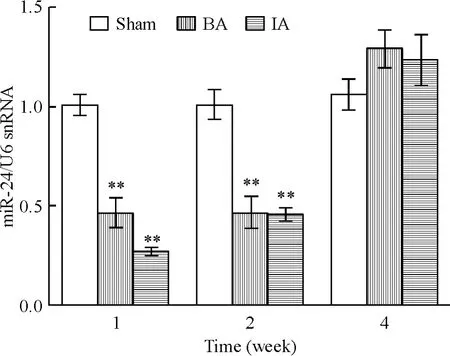
Figure 1. miR-24 was down-regulated in different areas of the hearts after MI. miRNAs were isolated in different areas of the infracted heart and sham-operated hearts 1,2,and 4 weeks after MI. qRT-PCR was performed to determine the level of miR-24. IA:infarct area;BA:border area. Mean ± SD. n =3. **P <0.01 vs sham group.圖1 小鼠心梗后局部組織miR-24 表達水平降低
2 miR-24 轉(zhuǎn)染改善心梗后心功能
構(gòu)建miR-24 慢病毒,心肌內(nèi)局部注射過表達miR-24,轉(zhuǎn)染慢病毒后3 d,用qRT-PCR 方法檢測轉(zhuǎn)染局部miR-24 表達水平,結(jié)果發(fā)現(xiàn)轉(zhuǎn)染miR-24 慢病毒后局部miR-24 表達水平較對照組升高(3. 98 ±0.50)倍(P <0.01),見圖2。超聲心動圖顯示,轉(zhuǎn)染miR-24 能顯著改善心梗后2 周小鼠心功能,心梗模型各組心功能較正常假手術(shù)組有明顯減低(P <0.01);miR-24 轉(zhuǎn)染組(LV-miR-24)與空白慢病毒轉(zhuǎn)染組(LV-GFP)比較,LVEF 和LVFS 明顯升高(P <0.05),miR-24 轉(zhuǎn)染組左室收縮末內(nèi)徑較空白慢病毒轉(zhuǎn)染組下降(P <0.05),而miR-24 轉(zhuǎn)染組左室舒張末內(nèi)徑與空白慢病毒轉(zhuǎn)染組間無明顯差異(P >0.05),見表1。
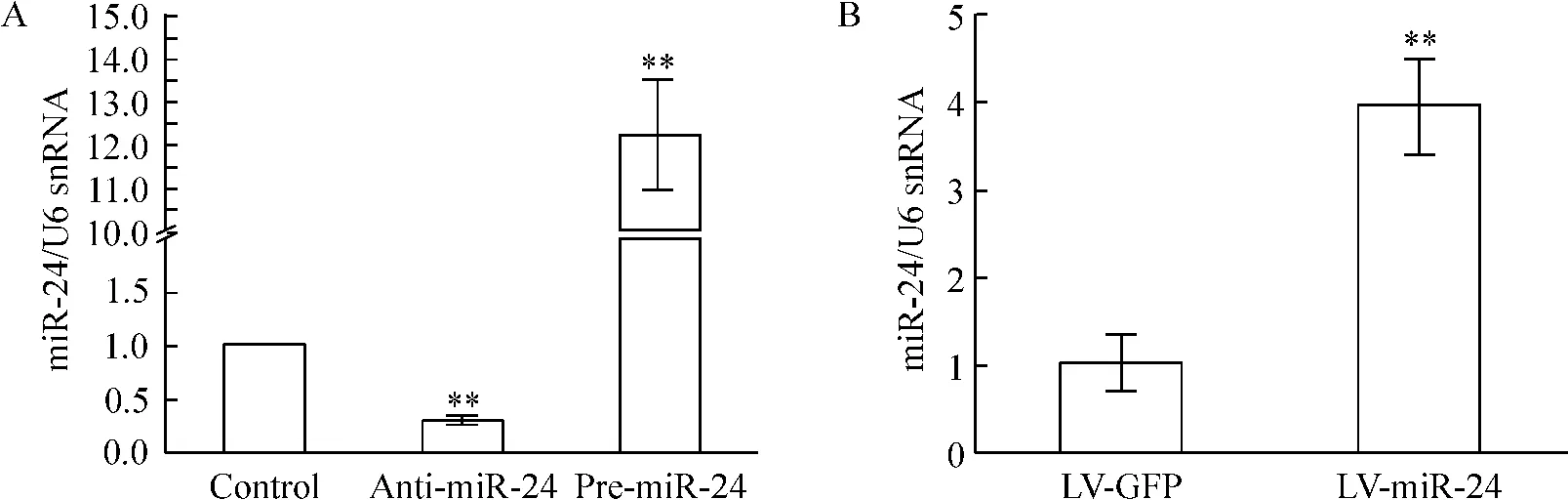
Figure 2. Expression of miR-24 in vivo and in vitro detected by qRT-PCR. A:cardiomyocytes (in vitro);B:border area (in vivo).Mean±SD. n=3. **P <0.01 vs control or LV-GFP.圖2 組織及細胞水平轉(zhuǎn)染miR-24 的表達情況

表1 miR-24 改善心梗后心功能Table 1. miR-24 improved heart functions after MI (mean±SD.n=9)
3 miR-24 轉(zhuǎn)染減少心梗面積
以上述攜帶miR-24 慢病毒轉(zhuǎn)染后的心梗模型,用Masson 染色方法檢測miR-24 轉(zhuǎn)染組及對照組心梗面積,結(jié)果發(fā)現(xiàn)miR-24 轉(zhuǎn)染能減少心梗2 周后心梗面積36.9%(P <0.01),并且轉(zhuǎn)染miR-24 后小鼠心梗區(qū)域的瘢痕組織明顯增厚,局部膨出減少,見圖3。
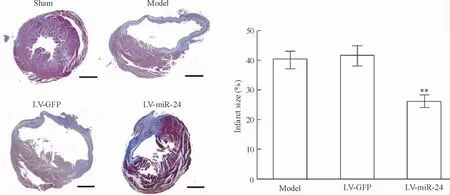
Figure 3. Lentiviral-mediated miR-24 transfection in vivo results in reduced scar formation after MI (Masson's trichrome staining,scale bar=1 mm). LV-GFP:lentiviral-GFP;LV-miR-24:lentiviral-miR-24.Mean±SD.n=6. **P <0.01 vs model.圖3 miR-24 轉(zhuǎn)染減少心梗后心梗面積
4 miR-24 轉(zhuǎn)染減少心梗區(qū)域細胞凋亡
心梗模型組織局部轉(zhuǎn)染miR-24,于心梗后1 周,使用TUNEL 組織染色檢測細胞凋亡情況,結(jié)果提示局部轉(zhuǎn)染miR-24 能明顯減少TUNEL 染色陽性細胞,抑制局部組織細胞凋亡,見圖4。
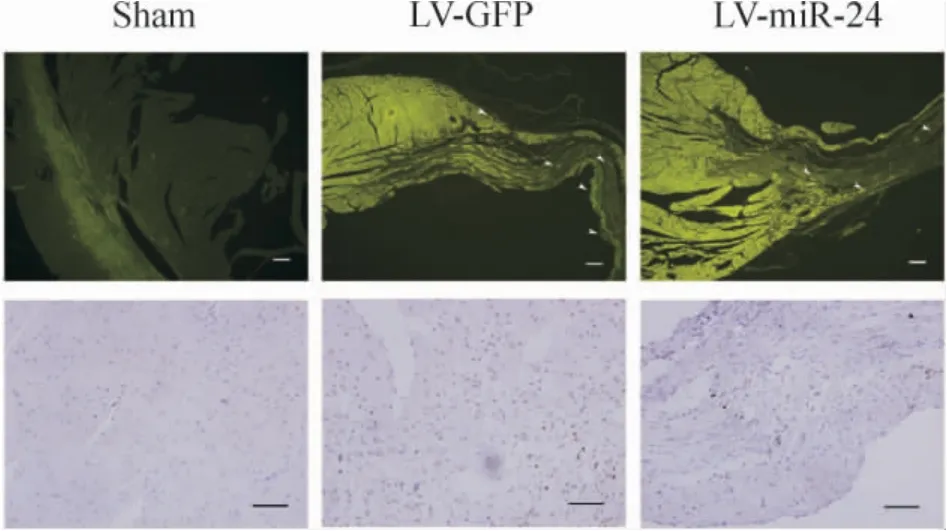
Figure 4. miR-24 decreased cell apoptosis in MI model (TUNEL staining). Upper figures:bar =100 μm;green indicates TUNEL positive cells,white arrows denote TUNEL positive areas. Lower figures:bar =50 μm;brown indicates TUNEL positive cells.圖4 miR-24 轉(zhuǎn)染減少心梗區(qū)域凋亡細胞數(shù)量
5 心肌細胞轉(zhuǎn)染miR-24 減少缺血缺氧造成的心肌細胞凋亡
對乳鼠心肌細胞應(yīng)用脂質(zhì)體轉(zhuǎn)染pre-miR-24 前體或anti-miR-24 抑制劑,qRT-PCR 檢測心肌細胞轉(zhuǎn)染效率,結(jié)果提示miR-24 前體能將心肌細胞miR-24表達水平升高到(12.2 ±1.3)倍(P <0.01),而miR-24 抑制劑則能將心肌細胞miR-24 表達水平降低到(29 ±4)%(P <0.01),見圖2。將轉(zhuǎn)染miR-24 后心肌細胞進行缺血缺氧處理,結(jié)果提示在心肌細胞過表達miR-24 能減少缺血缺氧誘導的心肌細胞凋亡,較對照組有顯著差異(P <0.01),而轉(zhuǎn)染miR-24 抑制劑則輕度增加心肌細胞在缺血缺氧條件下的凋亡(P <0.05),見圖5。
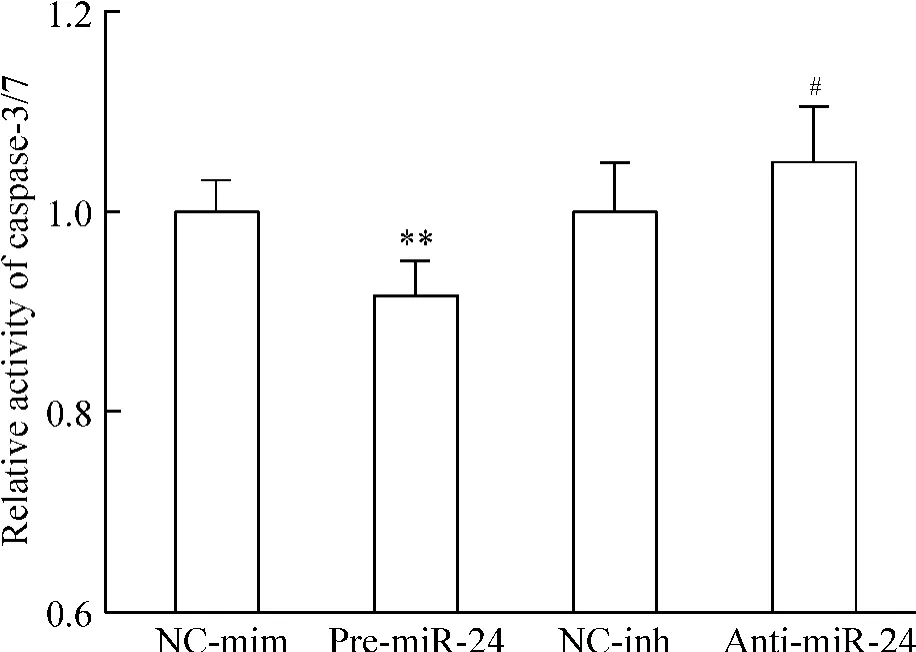
Figure 5. miR-24 inhibited cardiomyocyte apoptosis induced by hypoxia and serum deprivation. Cardiomyocytes transfected with pre-miR-24 mimic or anti-miR-24 inhibitor were treated with hypoxia and serum deprivation for 48 h. Caspase-3 and-7 activity was assayed by Caspase-Glo luminescence assay.NC-mim:negative mimic control;NC-inh:negative inhibitor control. Mean ±SD.n=9. **P <0.01 vs NC-min;#P <0.05 vs NC-inh.圖5 miR-24 抑制缺血缺氧造成的心肌細胞凋亡
6 表達譜芯片檢測miR-24 作用靶點
為明確miR-24 調(diào)控心肌細胞凋亡的具體作用靶位點,通過表達譜芯片檢測miR-24 轉(zhuǎn)染組及對照組心肌細胞mRNA 表達水平的差異。結(jié)果提示miR-24 轉(zhuǎn)染組相對對照組有49 個基因的表達水平達到1.5 倍以上升高,216 個基因表達水平0.5 倍以上降低。通過對miRNA 靶點數(shù)據(jù)庫TargetScan 的生物信息學分析,發(fā)現(xiàn)miR-24 的作用靶點中凋亡相關(guān)基因BCL2L11、ANK3 和SGPL1 的表達水平均下降,并且這3 個基因具有與miR-24 的保守結(jié)合位點,見圖6。
討 論
心肌細胞缺血缺氧造成的心肌細胞凋亡是心肌梗死后心功能不全,心衰的關(guān)鍵作用因素,如何減少心肌細胞在缺血缺氧條件下的凋亡成為現(xiàn)今心肌梗死研究的關(guān)鍵。本實驗以小鼠心肌梗死模型為體內(nèi)研究對象,以乳鼠心肌細胞缺血缺氧模型為體外研究對象,來研究miR-24 對心肌細胞缺血缺氧后凋亡水平的調(diào)控作用,并對其可能作用靶位點進行檢測和分析。現(xiàn)今多種細胞被使用來進行心肌細胞凋亡水平的研究,包括大鼠H9c2 細胞系、大鼠乳鼠原代細胞及小鼠心肌細胞,而大鼠乳鼠心肌細胞又以其收集培養(yǎng)技術(shù)的成熟穩(wěn)定被廣泛采用,而國內(nèi)外相關(guān)心肌組織及細胞實驗也大都采用小鼠心臟模型加大鼠乳鼠心肌細胞原代模型進行檢測[9]。
近年來的研究發(fā)現(xiàn),miRNAs 作為一種轉(zhuǎn)錄后調(diào)控因子,能夠同時靶向作用于多個不同通路中相關(guān)蛋白質(zhì)的信使RNA,從轉(zhuǎn)錄水平或轉(zhuǎn)錄后水平調(diào)節(jié)基因表達[10],進而從整體水平實現(xiàn)對細胞內(nèi)多種因子的表達乃至多條信號通路的“網(wǎng)狀”調(diào)控[11]。在心臟中miRNA 也被發(fā)現(xiàn)能調(diào)節(jié)心肌各種病理生理過程,包括心臟重塑、心臟發(fā)育、心肌纖維化、血管再生及心肌細胞凋亡[4,12]。現(xiàn)今已發(fā)現(xiàn)miR-499 能通過P53 通路作用于心肌細胞缺血再灌注損傷導致的凋亡,miR-21 通過抑制過氧化氫來調(diào)控心肌細胞死亡和凋亡[13]。本研究發(fā)現(xiàn)miR-24 能通過減少心肌細胞在缺血缺氧條件下的凋亡水平來改善心肌梗死后心臟重塑。miR-24 是一種在心肌組織中高表達的miRNA,在腫瘤細胞中,研究表明miR-24 能夠作用于DND1 蛋白,進而減少腫瘤細胞凋亡水平[14]。本實驗發(fā)現(xiàn)miR-24 在心肌梗死組織中表達量降低,心梗組織中轉(zhuǎn)染過表達miR-24 能夠減少心梗面積,改善心功能,并且在心肌細胞缺血缺氧模型中過表達miR-24 同樣能抑制心肌細胞凋亡水平。
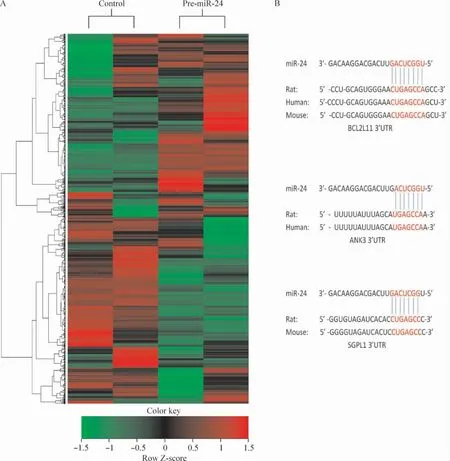
Figure 6. Possible targets of miR-24. A:hierarchical clustering of 265 mRNAs expressed in pre-miR-24 and control groups. The gene expression levels are represented by using a green-red color scheme,with the green corresponding to lower than median expression levels,the black corresponding to equal to median,and the red corresponding to higher than median expression levels. The scale indicates log10 ratio values. B:predicting putative miR-24 binding sites to apoptosis-regulating genes (potential complementary residues shown in red)by TargetScan.圖6 miR-24 作用于心肌細胞凋亡的可能靶位點
本實驗采用慢病毒心肌內(nèi)局部注射的方式進行轉(zhuǎn)染。許多方法都被使用轉(zhuǎn)染miRNA,比如微環(huán),腺病毒、寡核苷酸、antagomir 和慢病毒。脂質(zhì)體轉(zhuǎn)染起效快,但相對維持時間較短,而慢病毒能穩(wěn)定持續(xù)地表達miRNA,并能較長時間維持表型變化,近期文獻報道慢病毒心肌內(nèi)直接注射介導基因轉(zhuǎn)染,產(chǎn)生的炎癥和免疫反應(yīng)較低,具有很好的組織相容性,動物模型的死亡率沒有變化[15]。本實驗也發(fā)現(xiàn)慢病毒載體能有效轉(zhuǎn)染miRNA,并引起的毒副作用較小。
表達譜芯片由于其高靈敏度、高通量等優(yōu)點被廣泛使用檢測基因表達水平的變化,本研究通過對miR-24 作用靶點的表達譜芯片檢測及生物信息學分析,發(fā)現(xiàn)miR-24 可引起心肌細胞大量基因表達的變化,而相關(guān)凋亡調(diào)控,其可能作用于3 個凋亡相關(guān)基因BCL2L11、ANK3 和SGPL1。其中bcl-2 基因已被證明與細胞凋亡水平相關(guān)[16]。由于miRNA 作用靶點的多樣性,miR-24 可能通過一個或多個靶點基因作用于心肌細胞凋亡過程。
miRNA 不同于普通的蛋白受體阻滯劑,它能在整體上調(diào)控疾病進程,能成為良好的治療作用靶點,現(xiàn)已有部分臨床及臨床前實驗開展,取得了一定的成效。本研究發(fā)現(xiàn)miR-24 能作用于心肌細胞缺血缺氧條件下的凋亡過程,進而改善心梗后心功能,為臨床心梗治療提供了新的治療靶點,也為miRNA 的功能提供了新的作用機制。
[1] Qiu H,Liu JY,Wei D,et al. Cardiac-generated prostanoids mediate cardiac myocyte apoptosis after myocardial ischaemia[J]. Cardiovasc Res,2012,95(3):336-345.
[2] Abbate A,Narula J. Role of apoptosis in adverse ventricular remodeling[J]. Heart Fail Clin,2012,8(1):79-86.
[3] 莫 倩,李 丹,凌文華,等. miR-18a 對人主動脈內(nèi)皮細胞血管生成能力的影響[J]. 中國病理生理雜志,2012,28(7):1187-1191.
[4] Latronico MV,Condorelli G. MicroRNAs and cardiac pathology[J]. Nat Rev Cardiol,2009,6(6):419-429.
[5] Qin W,Shi Y,Zhao B,et al. miR-24 regulates apoptosis by targeting the open reading frame (ORF)region of FAF1 in cancer cells[J]. PLoS One,2010,5(2):e9429.
[6] 晏 浩,徐建軍,李文林,等.MicroRNA-30a 調(diào)控Beclin-1 對缺氧復(fù)氧乳鼠心肌細胞的保護效應(yīng)[J].中國病理生理雜志,2012,28(4):583-588.
[7] 夏文靜,黃藝儀,何建桂,等.急性心肌缺氧對乳鼠心肌細胞腦鈉尿肽表達的影響及其作用機制[J].中國病理生理雜志,2012,28(5):852-857.
[8] van Rooij E,Sutherland LB,Thatcher JE. Dysregulation of microRNAs after myocardial infarction reveals a role of miR-29 in cardiac fibrosis[J]. Proc Natl Acad Sci U S A,2008,105(35):13027-13032.
[9] Wang JX,Jiao JQ,Li Q,et al. miR-499 regulates mitochondrial dynamics by targeting calcineurin and dynaminrelated protein-1[J]. Nat Med,2011,17(1):71-78.
[10] 張 帥,李有杰,張 超,等. miRNA 在去甲斑蝥素致K562 細胞凋亡中的作用研究[J].中國病理生理雜志,2011,27(3):499-503.
[11] Gladka MM,da Costa Martins PA,De Windt LJ. Small changes can make a big difference-microRNA regulation of cardiac hypertrophy[J]. J Mol Cell Cardiol,2012,52(1):74-82.
[12]魏 聰,胡 兵,申 鍔,等.MicroRNAs 在心臟發(fā)育和疾病中的作用[J]. 中國病理生理雜志,2011,27(3):611-615.
[13] Zhu H,F(xiàn)an GC. Role of microRNAs in the reperfused myocardium towards post-infarct remodelling[J]. Cardiovasc Res,2012,94(2):284-292.
[14]Liu X,Wang A,Heidbreder CE,et al. MicroRNA-24 targeting RNA-binding protein DND1 in tongue squamous cell carcinoma[J]. FEBS Lett,2010,584(18):4115-4120.
[15]Yoshimitsu M,Higuchi K,Dawood F,et al. Correction of cardiac abnormalities in fabry mice by direct intraventricular injection of a recombinant lentiviral vector that engineers expression of α-galactosidase A[J]. Circ J,2006,70(11):1503-1508.
[16] Singh R,Saini N. Downregulation of BCL2 by miRNAs augments drug-induced apoptosis:a combined computational and experimental approach[J]. J Cell Sci,2012,125(Pt 6):1568-1578.

