基于三次相位建模的天波雷達污染校正

游 偉 何子述 陳緒元 胡進峰 何 茜

(1.電子科技大學電子工程學院，四川 成都 611731；2.南京電子技術研究所，江蘇 南京 210039)

引 言

天波超視距 (OTH) 雷達是一種具有超遠距離目標探測和信息獲取的雷達系統。天波OTH雷達不受地球曲率的影響，能實現數千公里的距離覆蓋，其對低空飛行器、海面艦船目標、隱身飛機、遠距離連續監測的能力，是其他雷達不可取代的[1]。國內外學者對天波超視距雷達展開了廣泛的研究，并取得很多實用的研究成果[1-8]。天波OTH雷達通常工作于高頻段(3～30 MHz)，與其他體制雷達不同，天波雷達信號傳播需要經過電離層的反射。由于電離層本身是一種運動的傳輸媒質，天波雷達的回波信號不可避免的受到電離層的影響，并將造成雷達回波信號頻譜的展寬。

海面的回波通常很強，這對海面的目標檢測構成威脅。尤其是對于慢速目標的檢測，由于其多普勒頻率靠近雜波譜，很容易被雜波掩蓋。由于天波雷達信號需要經過電離層的反射傳播，電離層自身的上下運動將對回波信號的頻譜產生頻移[7]。當雷達相干積累時間(CPI)較長或電離層上下運動加劇時，頻移將使得回波信號頻譜展寬，這稱為電離層污染。雖然有專門的頻率管理系統(FMS)支持[8-9]，使得雷達能夠自適應地選擇合適的工作頻率，在一定程度上緩解污染的問題，然而污染仍然不能完全避免。因此，研究天波污染的校正算法非常必要。

天波污染通常建模為一個乘性噪聲而不是加性噪聲。一般將天波超視距雷達的海雜波經過電離層傳播造成的污染建模為調頻信號的形式。因此，一般的天波污染校正的核心是要獲得雜波原始數據中的瞬時Bragg頻率分量的變化規律。獲得頻率變化規律后就可以通過與理論值的比較，對雜波原始數據做校正。在該領域已經提出許多算法，都取得了較好的效果。

BOURDLILLON[10]等提出使用最大熵譜法 (MESA)來對污染進行校正。這種算法將一個CPI內的雜波數據分成若干段，并且認為，在每個小段內的Bragg頻率是穩定的。在每個小段內使用高分辨譜估計算法分析得到其頻率。最后通過內插對CPI內的回波進行校正。這種算法在天波污染不大的情況下可以取得較好的效果，而當污染比較大的時候其效果則變差。

PARENT[11]等提出相位梯度法。這種算法很直觀，即直接對相位梯度進行能量平均。但是為了提高精度，需要多個發射波形進行平均，這對于傳統的雷達難以實現，將會增加雷達的復雜性。

HOWLAND[12]等提出使用Wigner-Ville分布 (WVD)算法獲得信號頻率并進行校正。該算法存在的問題是邊界上的點估計效果較差。

MARTIN[13]等提出使用Hankel降秩(HRR)算法來對雜波進行抑制。LU[14]等對此提出了改進。即先利用HRR方法求得雜波信號的瞬時頻率，利用所得到的瞬時頻率對污染后的雜波作校正。再對校正后的數據進行奇異值分解，以達到對雜波的抑制。這種級聯的處理使得雜波抑制效果有所提高。但是，使用HRR算法對雜波瞬時頻率的估計效果受到瞬時頻率的波動速度以及波動幅度的影響。當頻率波動不大并且速度較緩時，HRR算法能夠得到比較好的估計。而當變化稍大的時候其效果顯著下降，使得其補償效果變差。

PELEG等[15]提出使用離散多項式相位變換 (DPT)算法來獲得多項式信號的各階系數。劉顏回[16]、李雪[17]等將DPT算法應用于污染校正，并提出改進算法，都取得了很好的效果。但是這些改進措施增大了算法運算量，使得算法不能實時實現。

對被污染的回波，考慮其相位連續，可對信號分段。根據Weierstrass逼近定理，任意有限區間內的連續函數可由一個多項式無限逼近[18]。當分段較短，可以用一個三階多項式來逼近。因此，提出使用三次相位(CP)信號對天波雷達回波信號進行建模，并在此基礎上提出一種新的頻率估計算法對天波污染進行校正。該算法運行較快，能夠實時處理。同時，給出了算法的詳細處理流程和仿真結果，仿真結果表明：在天波污染比較嚴重，即頻率變化較大時，所提算法比HRR算法頻率估計更準確。因此，具有更好的污染校正效果，可以作為天波雷達污染校正的一種方案。

1 天波雷達回波信號模型

天波超視距雷達回波信號可以寫為如下形式

r(t)=c(t)+i(t)+s(t)+in(t)+n(t)

(1)

式中：c(t)為雜波(包括海雜波和地雜波)；i(t)為瞬態干擾；s(t)為感興趣的動目標回波；in(t)為各種非平穩干擾回波；n(t)為接收機內部熱噪聲。瞬態干擾以及非平穩干擾都將對動目標的檢測形成威脅，二者的抑制分別通過時域和空域的處理來實現，限于篇幅不做討論。

主要研究雜波的污染。已經證明，當海面被高頻信號照射時，回波信號將在固定的頻率處有很強的峰值，稱為Bragg峰。峰值的位置與雷達的工作頻率的關系為[6]

(2)

式中：g為重力加速度；fc為雷達工作頻率，Hz；c為光速，m/s.

根據Bragg模型，雜波分量的模型可以寫為

c(t)=ca(t)ej2πfbt+cr(t)e-j2πfbt

(3)

式中：ca(t)=Aa(t)ejφ(t)；cr(t)=Ar(t)ejφ(t)，Aa(t)和Ar(t)為信號幅度，φ(t)為考慮到電離層擾動引起的隨機相位。

電離層擾動引起的隨機相位，從頻域上看，是導致雷達回波信號的瞬時頻率隨機波動，從而造成頻譜展寬。對于艦船等低速目標而言，其頻譜通常很靠近Bragg譜，因此，雜波譜的展寬將使得艦船等目標的檢測變得非常困難。在進行艦船目標檢測時，需要對電離層的污染相位進行校正，而相位污染的校正可以等價的轉化為對信號瞬時頻率的估計。

2 三次相位信號的頻率估計

P.O’Shea[19]提出了三次相位信號的建模方法，并將其用于對天波雷達的回波信號進行建模，在此基礎上本文提出一種新的三次相位信號系數估計算法。三次相位信號可以寫為

s(t)=Aej(a0+a1t+a2t2+a3t3)

(4)

式中A為信號幅度。而信號的相位可以寫為

φ(t)=a0+a1t+a2t2+a3t3

(5)

式中，a0、a1、a2、a3為三次相位信號的系數，均為常數。

對信號相位求取延時有

φ(t+τ0)-φ(t-τ0)= 2a1τ0+4a2tτ0+

(6)

φ(t+τ0)+φ(t-τ0)= 2a0+2a1t+2a2t2+

(7)

定義算子

φ1(s,τ0)=s(t-τ0)s(t+τ0)s*(t)s*(t)

(8)

將相位關系代入，可以得到

(9)

(10)

得到了系數a3的估計值后，可以將該系數用于信號的補償，將三階相位項消除掉，則信號僅剩下二階相位項。對于一個二階相位信號，定義算子φ2(s,τ0)，有

φ2(s,τ0)=s*(t-τ0)s(t+τ0)

(11)

將信號的二階相位關系代入，有

φ2(s,τ0)=A2ej(2a1τ0+4a2τ0t)

(12)

DPT算法是對φ2(s,τ0)的FFT進行譜峰搜索，獲得系數a2.觀察式(12)可知，傳統的DPT算法采用一個延時來估計系數a2，這里將延時τ0作為變量，即τ0連續變化，而t固定，則對于式(12)給出的信號，瞬時頻率f可以寫為

2πf=2a1+4a2t

(13)

寫成離散形式，即2πf=2a1+4a2nT

(14)

式中T為采樣間隔。從式(14)可以看出，式(12)中信號的頻率與兩個系數呈線性關系，如果得到信號在兩個不同采樣點n1和n2的瞬時頻率f1和f2，則系數的估計值為

(15)

式中：

(16)

前面給出的是模擬信號下兩個算子的表達式，對于離散信號，設采樣下標為n，延遲系數為n0，則兩個算子可以表示為

φ1(s,τ0)=s(n-n0)s(n+n0)s*(n)s*(n)

φ2(s,τ0)=s*(n-n0)s(n+n0)

為了保證兩式中的下標n-n0和n+n0有意義，必須滿足1≤n+n0,n+n0≤N.

至此為止，就獲得了三次相位信號的各個系數的估計值，即可對該信號的頻率作估計，其瞬時頻率可以寫為

(17)

(18)

從式(18)可以看出，如果存在估計誤差，則補償后的信號也會引入相應的相位剩余。忽略三階項，按照前述算法，以延時τ0為變量，所得信號瞬時頻率f可以寫為

2πf=2a1+4a2t+6aΔ3t2

(19)

寫成離散的形式，則一階與二階系數可以估計為

(20)

從式(20)看出，當三階系數存在誤差時，該誤差傳遞給一階和二階系數，誤差的大小與三階系數估計的誤差近似成正比關系。

3 天波污染校正算法

天波污染校正的關鍵是要捕獲Bragg譜峰瞬時頻率的變化，即要獲得某一個Bragg譜線的瞬時頻率。獲得瞬時頻率后，將電離層引起的污染相位補償掉即可實現校正。一般的污染校正算法都基于這一思想。

一個被污染的Bragg信號分量可以表示為

(21)

式中m(t)為所需要求解的瞬時頻率擾動。在獲得瞬時頻率后即可減去理論的Bragg頻率而獲得該擾動值，并可通過式(22)作校正，得到校正后的信號成分xc(t)：

(22)

這里利用第2節的三次相位信號來對Bragg分量進行建模，并將其用于電離層污染的校正。由于實際的Bragg分量并不是理想的三次相位，因此，這里采用分段的思想，將回波數據分成若干段，對每段內用三次相位進行建模，并獲得其瞬時頻率。基于三次相位建模的校正算法流程如圖1所示，可以描述為：

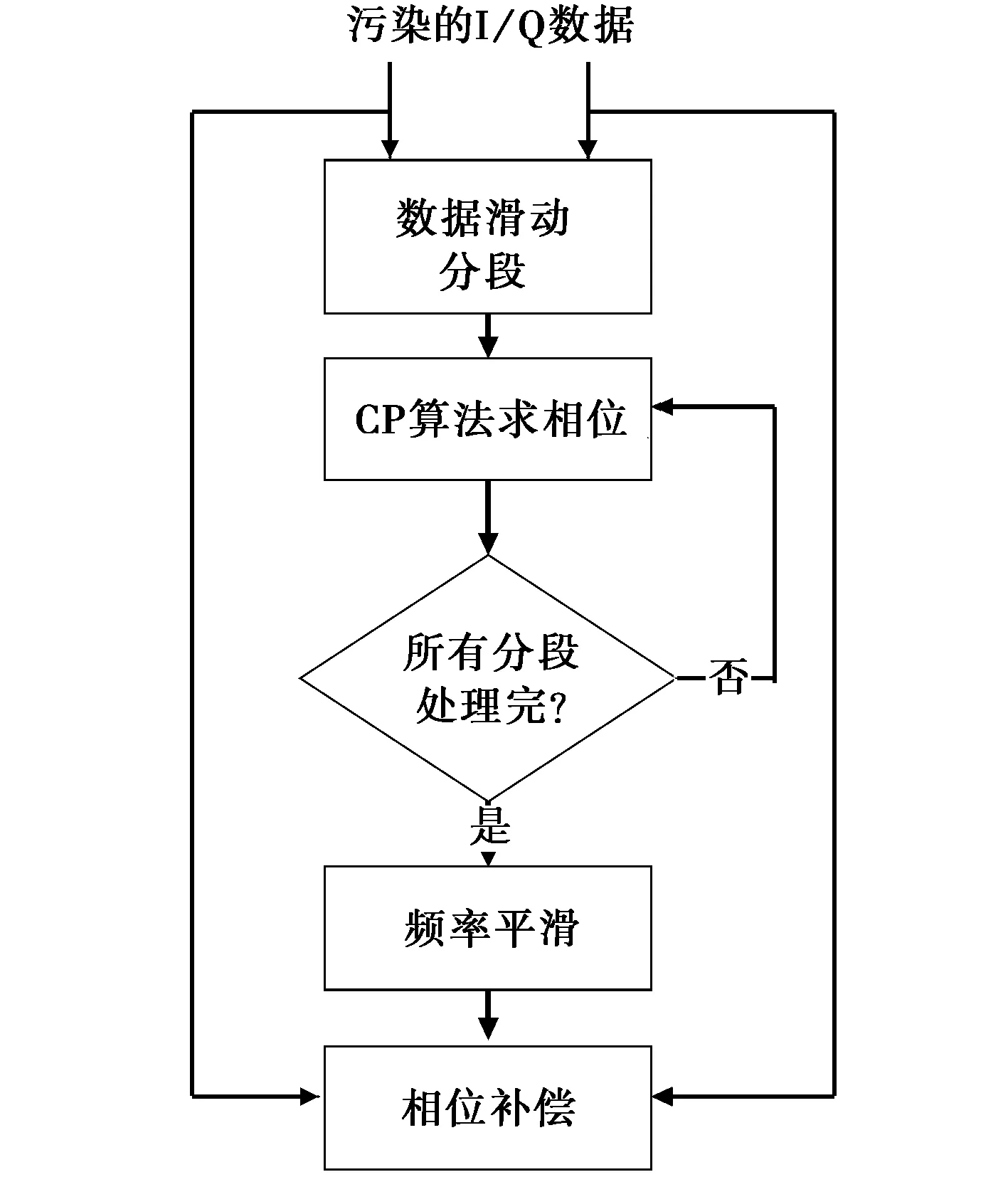
圖1 基于CP的電離層污染補償算法

1) 對某個距離單元一個CPI內的數據做FFT變換，將數據變換到頻域。

2) 在給定頻域區間進行譜峰搜索，濾出最強的譜峰，用于提取頻率信息。

3) 對提取出的譜峰做IFFT將數據變換到時域，然后將數據分段，對每段數據求取瞬時相位，每段數據還可以有交疊以便對估計結果進行平滑。

4) 對每段所得到的頻率數據進行平均，得到每個采樣點的瞬時頻率。

5) 利用瞬時頻率對回波作校正。

4 仿真結果

本節將給出基于三次相位建模的污染校正仿真結果。其中雷達工作頻率為15 MHz，雷達脈沖重復頻率為5 Hz，積累256個脈沖數，則其相干積累時間為51.2 s.兩個Bragg分量的幅度分別為5和15.雜噪比為25 dB，動目標多普勒頻率為0.59 Hz，信噪比為8 dB.天波雷達回波被信號γ(t)所污染(即調制)，

γ(t)=ejB1cos(2πfm1t+θ0)

(23)

式中：B1=0.5；fm1=0.25.

仿真結果如圖2～5所示。其中圖2給出了被污染的某距離單元的回波頻譜，可以看出，兩個Bragg譜峰都被展寬了，并且掩蓋了動目標的頻譜，使得目標無法檢測。將負的Bragg峰分離出來進行處理，用所提算法估計其瞬時頻率，圖3(見1061頁)給出了基于所提算法的瞬時頻率估計與理論值的比較。其中，每段數據的長度為16個數據點，每段數據有兩點的數據重疊，因此，總共處理的數據為121段。從圖3可以看出， 新算法能夠很好的跟蹤頻率的變化，具有很好的頻率估計性能。

圖2 被污染的天波雷達回波譜

圖4是利用圖3所得頻率估計值進行補償后的頻譜。可以看出，經過補償后，兩個Bragg譜峰都變窄了，臨近的目標很容易區分，證明算法具有較好的補償效果。圖5給出HRR算法補償后的頻譜。由于HRR算法在頻率擾動較大時不能實現頻率準確跟蹤，因此，在此情況下，HRR算法不能實行有效的補償。

圖4 新算法校正后的頻譜

圖5 HRR算法校正后的頻譜

5 結 論

將三次相位信號用于對天波雷達的回波信號進行建模，在此基礎上提出一種新的頻率估計算法，并將所提算法應用于天波污染的校正。該算法的參數估計通過FFT進行，運算速度較快，仿真表明：對于一個256點的數據，算法可以在0.25 s左右完成校正處理。因此，所提算法可以進行實時處理。

另外，還給出了算法的具體流程及仿真結果。仿真結果表明：當天波污染較大時，所提算法比HRR算法頻率估計要準確，因而具有更好的污染校正性能。

[1] 周文瑜, 焦培南. 超視距雷達技術[M]. 北京:電子工業出版社, 2008.

[2] 陳希信, 黃銀河. 高頻雷達回波信號去電離層污染[J]. 現代雷達, 2007, 29(2): 41-43.

CHEN Xixin, HUANG Yinhe. Ionosphere decontamination of high frequency radar echoes [J]. Modern Radar, 2007, 29(2): 41-43. (in Chinese)

[3] 蘇洪濤, 劉宏偉, 保 錚, 等. 天波超視距雷達機動目標檢測方法[J]. 系統工程與電子技術，2004, 26(3): 283-287.

SU Hongtao, LIU Hongwei, BAO Zheng, et al. Method for maneuvering target detection in HF over-the-horizon radar[J]. Systems Engineering and Electronics, 2004, 26(3): 283-287. (in Chinese)

[4] 周萬幸. 天波超視距雷達發展綜述[J]. 電子學報, 2011, 39(6): 1373-1378.

ZHOU Wanxing. An overview on development of skywave over-the-horizon radar[J]. Acta Electronica Sinica, 2011, 39(6): 1373-1378. (in Chinese)

[5] 姜 維, 鄧維波. 分段多項式建模校正電離層相位污染算法研究[J]. 電波科學學報, 2011, 26(5): 855-863.

JIANG Wei, DENG Weibo. Ionospheric phase contamination correction method based on piecewise polynomial phase modeling[J]. Chinese Journal of Radio Science, 2011, 26(5): 855-863. (in Chinese)

[6] KHAN R. Ocean-clutter model for high-frequency radar[J]. IEEE Journal of Oceanic Engineering, 1991, 16(2): 181-188.

[7] 焦培南, 凡俊梅, 吳海鵬, 等. 高頻天波返回散射回波譜實驗研究[J]. 電波科學學報, 2004, 19(6): 643-648.

JIAO Peinan, FAN Junmei, WU Haipeng, et al. The experimental research of the Doppler spectrum by HF skywave backscattering[J]. Chinese Journal of Radio Science, 2004, 19(6): 643-648. (in Chinese)

[8] BAZIN V, MOLINIE J P, MUNOZ J, et al. NOSTRADAMUS: An OTH radar[J]. IEEE Aerospace and Electronic Systems Magazine, 2006, 21(10): 3-11.

[9] EARL G F, WARD B D. Frequency management support for remote sea-state sensing using the Jindalee skywave radar[J]. IEEE Journal of Ocean Engineering, 1986, 11(2): 164-172.

[10] BOURDLILLON A, GAUTHIER G. Use of maximum entropy spectral analysis to improve ship detection over-the-horizon radar[J]. Radio Science, 1987, 22(2): 313-320.

[11] PARENT J, BOURDLILLON A. A method to correct HF skywave backscattered signals for ionospheric frequency modulation[J]. IEEE Transaction on Antennas Propagation, 1988, 36(1): 127-135.

[12] HOWLAND P E, COOPER D C. Use of the Wigner-Ville distribution to compensate for ionospheric layer movement in high-frequency sky-wave radar systems[J]. IEE PROCEEDINGS-F, 1993, 140(1): 29-36.

[13] MARTIN W Y, KHAN R, SON L N. A singular value decomposition (SVD) based method for suppressing ocean clutter in high frequency radar[J]. IEEE Transaction on Signal Processing, 1993, 41(3): 1421-1425.

[14] LU K, LIU X Z, LIU Y T. Ionospheric decontamination and sea clutter suppression for HF skywave radars[J]. IEEE Journal of Oceanic Engineering, 2005, 30(2): 455-462.

[15] PELEG S, FRIEDLANDE B. The discrete polynomial-phase transforms[J]. IEEE Transactions on Signal Processing, 1995, 43(8): 1901-1914.

[16] 劉顏回, 聶在平, 趙志欽. 改進的分段多項式建模的電離層相位去污染新方法[J]. 電波科學學報, 2008, 23(3): 476-483.

LIU Yanhui, NIE Zaiping, ZHAO Zhiqing. A new method based on improved piecewise polynomial phase model to correct ionospheric phase contamination[J]. Chinese Journal of Radio Science, 2008, 23(3): 476-483.(in Chinese)

[17] 李 雪, 鄧維波, 焦培南, 等. 多項式建模解電離層相位污染階數選擇新方法[J]. 電波科學學報, 2009, 24(6): 1094-1098.

LI Xue, DEND Weibo, JIAO Peinan, et al. Novel order-select method of polynomial modeling for ionosphere phase perturbation correction [J]. Chinese Journal of Radio Science, 2009, 24(6): 1094-1098. (in Chinese)

[18] 嘉德克 B K. 多項式一致逼近函數導論[M]. 沈燮昌, 譯. 北京: 北京大學出版社, 1989.

[19] O’SHEA P. A fast algorithm for estimating the parameters of a quadratic FM signals [J]. IEEE Transactions on Signal Processing, 2004, 52(2): 385-393.