“自動控制原理”課程的頻域部分教學探討

2012-06-21 09:57:56丁世宏楊年法趙德安

電氣電子教學學報 2012年3期

丁世宏，楊年法，趙德安，馬莉

(江蘇大學電氣信息工程學院，江蘇鎮江 212013)

“自動控制原理”課程數學性強，理論概念抽象，具有一定的深度和學習難度[1，2]。盡管關于“自動控制原理”課程教學方面已經有很多相關的文獻論及，但大部分論文都是針對整個課程的教學探討[3，4]，很少有專門針對某一章節而討論其具體存在的教學問題，以及相對應的解決策略。

在“自動控制原理”的教學中，頻域分析部分占有很大的比重，知識多，難度高。筆者針對“自動控制原理”頻域分析教學部分，總結出了目前關于這一部分教學中較為常見的幾個問題，并探討了一些相對應的解決策略。

1 頻域部分教學現狀

控制系統的頻域部分主要包括如下內容:①頻率特性的概念;②典型環節的頻率特性及頻率特性曲線的繪制(伯德圖和奈奎斯特曲線);③基于伯德圖和奈奎斯特曲線的穩定性判據;④利用頻域特性曲線分析系統的性能。

根據筆者調研，很多學生反映有些知識點在數學形式上比較復雜抽象，很難掌握。“自動控制原理”頻域部分可能引起學生理解困難的知識點，可以概括為以下四個方面。

1)對數頻率特性坐標系

傳統坐標系標度都是以十進制為單位，而這一部分所考慮的對數頻率特性坐標系標度以對數刻度來表示。十進制單位中的距離1，在對數頻率特性坐標系中以十倍頻程來表示。該知識點看似簡單，但是由于顛覆了傳統觀念中對距離的認識，因此在實際計算過程中很容易出錯。

2)幅角定理的理解

在講解奈奎斯特穩定判據的時候，首先要介紹幅角定理。由于幅角定理比較抽象，而奈奎斯特穩定判據正是建立在幅角定理的基礎之上，因而影響了學生對奈奎斯特穩定判據的理解和應用。

3)原點處有開環極點時的穩定判據

若系統的開環傳遞函數在原點處沒有極點，學生利用奈奎斯特穩定判據，一般都能夠準確的給出穩定與否的判別。但是，若系統的開環傳遞函數在原點處含有極點，從課后作業來看，錯誤率較高，特別是開環傳遞函數帶有兩個積分器的情形。

4)穩定裕度

學生對系統的穩定裕度具有思維定勢，仍然局限在時域內，即認定特征值離虛軸距離越遠，系統的穩定裕度越高。然而，若利用幅值裕度和相角裕度的概念來講解穩定裕度時，盡管有數學指標作為參考，但是對這兩個穩定裕度的理解仍然不夠深刻。

根據調查分析，產生上述問題的客觀原因主要有以下兩點:①系統的頻率響應主要分析輸入為正弦信號時，系統的輸出所具有的性質。因此，頻域響應的分析主要取決于系統的模型。由頻域部分的教學內容可知，研究對象是以傳遞函數為數學模型來描述的線性系統。教學方式主要是推導數學公式，得到數學上的結果。學生通常對繁瑣的數學公式推導難以理解，影響了課程的學習和知識點的理解;②課本中的例子很少涉及生活中的實際應用系統。使得學生誤認為頻域分析理論在實際過程之中沒有應用價值，對這一部分內容學習興趣下降。

2 頻域部分的教學探討

筆者針對上述教學中普遍存在的問題，建議采用如下有針對性的教學方法進行改進。

1)理論形象化，訓練反復化

由于基于數學模型和系統分析的理論內容占據課程內容的80%以上，首先要向學生強調理論內容的重要性。根據筆者的教學經驗，在每一節課前20分鐘的時間中學生的注意力最為集中。為了充分利用這段時間，應該將大部分較難理解的理論知識集中在這一時間段講解。在講解理論知識時，推導數學公式之余，應該要注重結合圖形表格來闡述，使得理論形象化。

在余下的時間，學生的注意力將有一定的分散。此時，不斷地采用例子對所講授的知識點進行反復訓練。甚至可以嘗試讓學生自己走上講臺練習。此外，還應當注重結合生活中的實際應用，利用前面的理論知識進行實例分析，從而提高學生的學習興趣，增強教學效果。

2)突出教學主線

教師在講解過程中，每一節課可能涉及到多個知識點。此時，學生的注意力可能會平均分散到多個知識點不易抓住重點。教師應該對這些知識點進行重組編排，保證在每一節課的講授過程中，始終以一個知識點為主線帶動其他知識點。這樣可以加深學生的記憶，有益于學生對知識點的理解。

3)將仿真和實際相結合

為了加強學生對知識點的理解能力，需要尋找一些易于建模的實際系統作為實例，并在這些實例上驗證所學的知識點。首先，對系統進行理論分析，并利用Matlab仿真軟件，給出實際系統的頻域分析結果。這一過程不僅可以加深學生對理論的理解，而且可以鍛煉學生的編程能力。其次，通過對該實際系統進行實驗研究，建立實驗平臺，驗證仿真分析的準確性，培養了學生的動手能力。此外，還可嘗試在科普期刊中尋找涉及到自動化控制方面的文章，向學生介紹文章中所應用到的“自動控制原理”中的理論知識。

3 教學實踐

現在，我們對頻域分析教學中存在的問題，歸納出相應的解決方法，大致分為以下三個步驟:①爭取在一堂課的前20分鐘以內講授完該節課有關知識點。在理論分析時，注意利用圖形或者表格，使得理論問題形象化和具體化;②構建基于實際模型的例子，利用所講授的知識點進行理論分析，并在Matlab上進行仿真驗證;③進行實驗教學，將理論知識實際化，使得學生懂得學以致用，最終理解所學習的知識點。下面以頻域分析中的“穩定裕度”為例，給出一個具體的教學案例。

1)闡述相角裕度和幅值裕度的基本概念

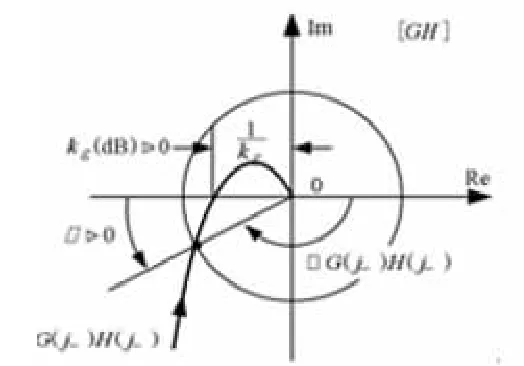
圖1 奈奎斯特圖

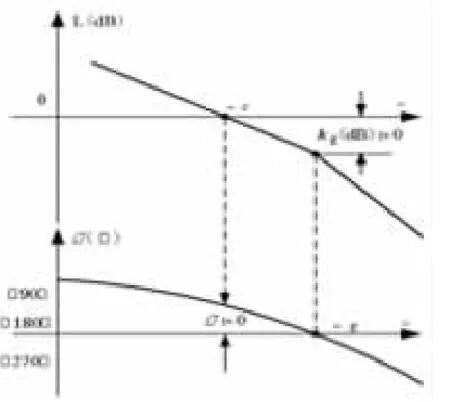
圖2 伯德圖

2)尋找一個滿足理論分析和實際實驗的例子

此處，我們給出如圖3所示的RLC電路系統的模型例子，給出其頻率特性的分析結果。

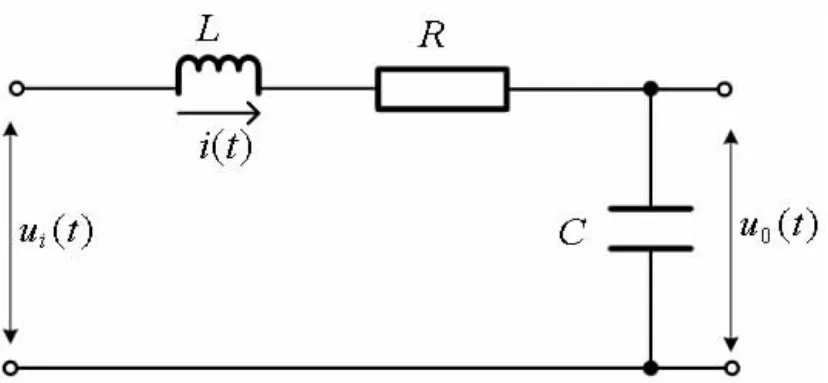
圖3 RLC串聯電路圖

在圖3中，輸入為ui(t)，輸出為u0(t)。分析可得開環傳遞函數為G(s)H(s)=1/(LCs2+RCs+1)，其頻域特性為

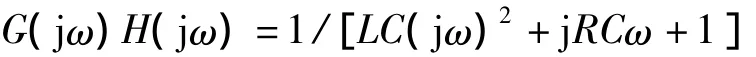
該系統是一個典型的二階系統，很容易利用勞斯判據判別系統穩定與否。為了驗證穩定裕度，首先利用勞斯判據，分別求出穩定裕度好、穩定裕度差、臨界穩定和不穩定幾種情況對應的參數L，C，R的具體值。然后驗證這些參數下的穩定裕度，并通過Matlab仿真，作出對比。

3)通過搭建電路來驗證上述的理論分析。

4 結語

筆者根據以往的教學經驗以及“自動控制原理”課程的特點，總結了該課程頻域部分教學中普遍存在的問題，并討論了這些問題存在的原因。與此同時，筆者還有針對性地介紹了一些解決這些問題的方法。我們通過一個教學案例，闡述了如何運用所介紹的教學方法解決已有的教學問題。

[1]胡壽松.自動控制原理(第5版)[M].北京:科學出版社，2007

[2]高國燊，余文烋.自動控制原理(第2版)[M].廣州:華南理工大學出版社，2005

[3]孟令雅.自動控制理論教學漫談[J].南京:電氣電子教學學報，2006，28(1)，48-50

[4]陳旭，林國余.“自動控制原理”課程教學研究與探索[J].南京:電氣電子教學學報，2009，31(5):26-27