信號與系統中抽樣定理的教學探討

楊巧寧，李學斌，王學偉

(北京化工大學信息科學與技術學院，北京 100029)

抽樣定理是“信號與系統”課程中重要的知識點，在連續時間信號的頻域分析中講解，國內外教材中均對其詳細論述[1-4]。但是對初學學生來說，這個知識點的理解不夠透徹，難以獲得正確應用。為了要讓學生深刻理解抽樣定理，本文以時域抽樣定理為例討論教學過程的設計。

1 抽樣和抽樣定理

“抽樣”就是利用周期抽樣脈沖p(t)從連續信號f(t)中抽取離散樣值的過程，得到的離散信號為抽樣信號，也稱為采樣信號，以fs(t)表示。抽樣過程的數學模型就是連續信號與抽樣脈沖序列相乘。圖1是連續信號時域抽樣和從抽樣信號恢復原連續信號的框圖。

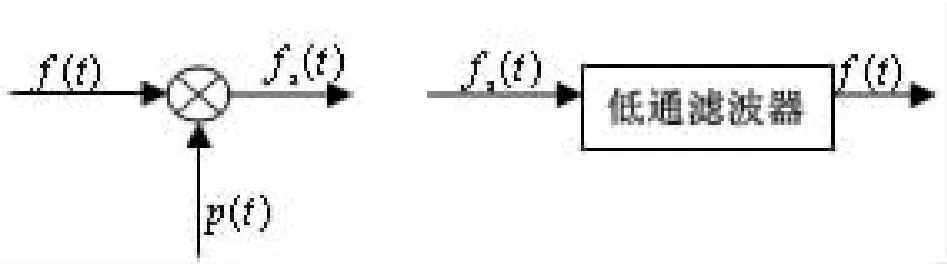
圖1 連續信號時域抽樣和連續信號恢復框圖

連續信號時域抽樣后，其頻譜Fs(ω)是連續信號頻譜F(ω)以抽樣頻率ωs為間隔周期重復的結果，幅度受到抽樣脈沖p(t)的傅里葉級數系數Pn的加權[5]。

抽樣定理的內容是:對于帶限信號，其頻譜占據－ωm～+ωm的范圍，若信號可用抽樣值來唯一地表示，則必須滿足ωs≥2ωm或者Ts≤1/2fm

如果抽樣頻率滿足抽樣定理，則抽樣信號通過截止頻率為ωc(ωm＜ωc＜ωs－ωm)的低通濾波器，可由抽樣信號fs(t)無失真復原信號f(t)。本文以理想低通濾波器恢復為例。

2 課堂教學方法

2.1 問題法

課堂教學中把內容問題化，以問題串起本節內容，可以幫助學生循序漸進理解知識點。整節內容提煉為五個問題，它們相互承接，概況了全部內容。

(1)為什么抽樣?

這個問題讓學生認識抽樣的重要性和必要性，認識抽樣的目的和意義。

數字信號處理技術的優勢和快速發展使得數字設備和數字媒體廣泛應用，如手機、MP3、CD和DVD等。抽樣是連續信號變成數字信號非常關鍵的一步。在講解抽樣的過程和抽樣的數學模型后，以第二個問題引出下一個重要知識點。

(2)抽樣信號時域發生什么變化(抽樣信號與連續信號的關系)?頻域發生什么變化(抽樣信號頻譜和連續信號頻譜的關系)?

這個問題可幫助學生理解抽樣帶來信號的實質變化。結合圖形演示法講解。詳細過程見文獻[5]。

抽樣過程:

其物理意義是沖激抽樣信號的傅立葉變換是連續信號頻譜嚴格的周期重復。重復周期為抽樣頻率ωs，幅度受到常數1/Ts的加權，頻譜形狀不變。

(3)抽樣信號是否保留連續信號的全部信息?

抽樣信號在時頻域變化講解后，以問題啟發學生進一步思考抽樣的實質，第二問題和第三問題聯系緊密，都為了說明抽樣定理實質。

根據學生實時課堂的回答繼續以問題啟發，比如，抽樣得到連續信號某些位置上的值，抽樣信號是否應該反映連續信號的全部特征?為什么?要保留連續信號的全部信息和哪個指標有關?緊接著引出第四個問題，即引出重要知識點—抽樣定理。

(4)抽樣頻率應該為多大?

這個問題幫助學生理解抽樣定理研究的對象和實質，以及抽樣定理的出發點。抽樣必須保留連續信號的全部信息，抽樣頻率如何影響信息的保留度?實際抽樣中，如何確定抽樣頻率?結合案例法和圖形演示法講解。在這里給出抽樣定理的內容。

抽樣定理理論給出后，可以再回到案例上進行重新分析，進一步加強對抽樣定理的理解，可以結合實踐法加深理解。

(5)如何從抽樣信號不失真的恢復連續信號?

若滿足抽樣定理，抽樣信號唯一的表示連續信號，則可由抽樣信號不失真的恢復連續信號，如何恢復?結合圖形演示法進行講解。

如果能得到連續信號的完整頻譜，則就得到了連續信號。滿足抽樣定理的條件下頻譜不交疊，則可利用理想低通濾波器得到連續信號的完整頻譜。理想低通濾波器的幅度和截止頻率如何確定?理想低通濾波器(ωc－ωm≥ωc≥ωm):

2.2 案例法

理論分析講解比較抽象，學生的理解不夠透徹。如果對實際案例的應用采用直觀形象的方法說明，初學學生對案例引入的知識點理解有幫助很大。

我們可以在提出第3、4和5個問題提出的時候，利用學生常見的實際信號:歌曲(語音信號)和照片(圖像信號)，給出這兩種實際信號不同抽樣率下的結果。

圖2所示是不同抽樣率下圖像的效果，包含圖像失真嚴重、不失真及處于兩者之間的圖像效果。這些圖像讓學生直觀看到抽樣率的大小對信號的影響，對信號的保留或失真程度。明白抽樣頻率不夠大時，重現信號會失真，如圖2(a)和圖2(b)所示。頻率越大信號更接近原始信號，當大到一定值時，重現信號的信息已保留很好，再大時信號差異不明顯，就會帶來冗余，如圖2(c)和圖2(d)。學生便會提出:抽樣頻率應滿足什么條件，應依據什么來選擇?

圖2 不同抽樣率的圖像

我們給出一段學生熟悉的音樂，采用不斷降低抽樣頻率來收聽音樂效果。讓學生從聽覺效果上分析抽樣率對信號的影響，如圖3所示。這里選擇抽樣頻率時應包含:圖3(a)為滿足采樣定理的語音;圖3(b)為不滿足采樣定理的頻譜交疊的語音;如圖3(c)為不滿足采樣定理的抽樣頻率，且過小原始語音丟掉很多的語音，基本上聽不出是什么旋律。

圖3 不同抽樣率對語音的影響

2.3 實踐法

我們利用Matlab實現抽樣定理的程序，對圖像和語音這非典型一維信號進行抽樣。課堂上現場演示，讓學生任意給定抽樣頻率。給出滿足、不滿足和臨界滿足采樣定理的情況，如圖4所示。

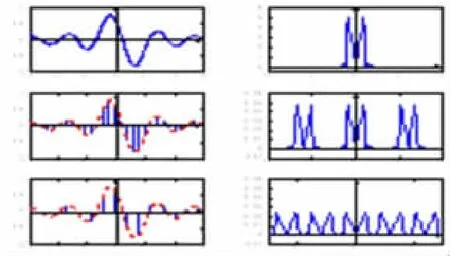
圖4 信號抽樣例子

上圖中給出了其中一個處理結果。左邊一列是不同抽樣率下的原始時域信號，右邊一列是對應的頻譜。這種方法給學生展示了實時可變的動態圖形。讓其了解抽樣信號的變化、頻譜的變化、抽樣率對信號的影響、不同抽樣率的信號恢復效果及與原信號之間的關系。

2.4 圖形演示法

在問題法(2)的理論講解完后，以圖形的形式演示抽樣過程，如圖5所示。學生可以直觀看到怎樣抽樣、抽樣信號和原信號的關系、抽樣后頻域的變化及抽樣信號頻譜與原信號頻譜的關系。

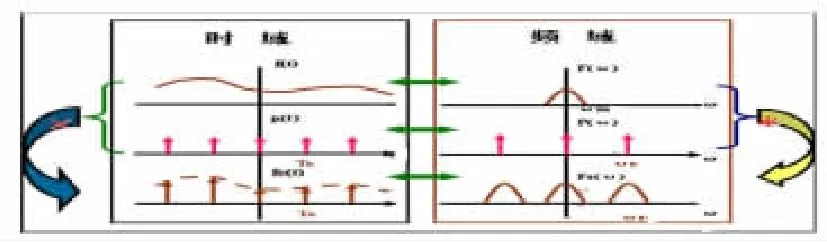
圖5 抽樣過程及頻譜變化

在問題法(4)的抽樣定理內容講解之前，通過圖形演示分析。要得到原信號完整頻譜，抽樣頻率應滿足的條件，從而引出抽樣定理內容。在問題法(5)之前可借助滿足采樣定理的圖形演示，分析恢復原始信號的方法原理如圖6所示。

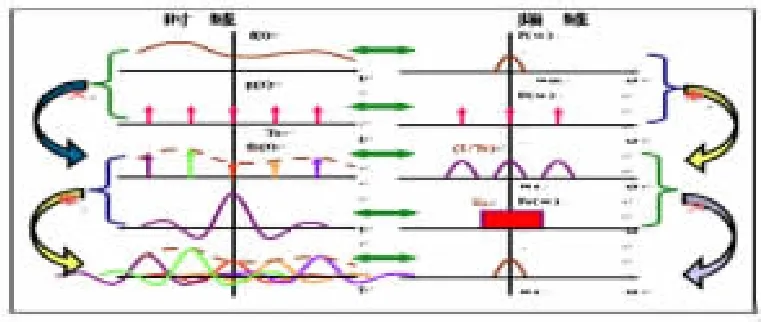
圖6 恢復信號的方法原理

3 結語

本文通過問題法、案例法和實踐法圖形演示法講解抽樣定理，幫助學生掌握和深刻理解抽樣定理的內容。問題法有利于啟發思維，激勵創新，圖形演示法有利于得到直觀認識，案例法有利于理解實際應用，實踐法有利于倡導活學活用。我們將這些方法有機結合來講述抽樣定理，對教科書內容給予很好的補充，取得了很好的教學效果。

[1]奧本海姆著，劉樹棠譯.信號與系統(第二版)[M].西安:西安交通大學出版社，1998

[2]管致中，夏恭恪，孟橋.信號與線性系統(第四版)[M].北京:高等教育出版社，2004

[3]吳大正，信號與線性系統分析(第四版)[M].北京:高等教育出版社，2006

[4]陳后金，胡健等.信號與系統[M].北京:高等教育出版社，2003

[5]鄭君里，應啟珩，楊為理.信號與系統[M].北京:高等教育出版社，2000