關(guān)于無功功率的討論

田社平，陳洪亮

(上海交通大學(xué)電子信息與電氣工程學(xué)院，上海 200240)

在正弦穩(wěn)態(tài)電路中，與功率有關(guān)的概念包括瞬時(shí)功率、平均(有功)功率和無功功率、表觀功率、復(fù)功率等，其中平均功率是指電路實(shí)際消耗的功率，其對應(yīng)的電能將轉(zhuǎn)換為電、磁能量之外的能量如熱能等消耗掉，具有十分明顯的物理含義;而無功功率作為一種功率的概念，雖然具有功率的量綱，但它終究不是實(shí)際作功的功率，其物理含義卻不那么明顯。在教學(xué)過程中，常有學(xué)生提出“什么是無功功率?”和“無功功率與瞬時(shí)功率有何關(guān)系?”等問題。本文結(jié)合教學(xué)實(shí)踐，試對上述問題作一討論。

在電工技術(shù)中，無功功率的定義首先源自對儲(chǔ)能元件無功功率的定義。對電感元件，無功功率定義為電感兩端正弦穩(wěn)態(tài)電壓、電流有效值的乘積;對電容元件，無功功率定義為電容兩端正弦穩(wěn)態(tài)電壓、電流有效值的乘積的負(fù)值[1-5]。這說明無功功率不僅有大小之分，而且還有正負(fù)之分。

1 無功功率的實(shí)質(zhì)

1.1 無功功率之正負(fù)號的含義

無功功率的正負(fù)號反映了電容存儲(chǔ)的電能和電感存儲(chǔ)的磁能之間可以互相轉(zhuǎn)化。利用圖1對無功功率的正負(fù)號可作進(jìn)一步說明。圖1(a)是LC兩個(gè)元件的串聯(lián)。對照電容和電感的瞬時(shí)功率曲線，可以看出:電路中的電容在吸收功率的同時(shí)，電感恰好在釋放功率;而電感在吸收功率的同時(shí)，電容恰好在釋放功率。在圖1(b)所示的并聯(lián)電路中還包含電阻元件。對照電容和電感的瞬時(shí)功率曲線，可以看出:盡管并非在所有的時(shí)間段電容和電感在吸收或釋放功率正好相反，但在一部分時(shí)間段內(nèi)電路中的電容在吸收功率的同時(shí)，電感恰好在釋放功率;而電感在吸收功率的同時(shí)，電容恰好在釋放功率。我們由此可以得出:在存在兩種儲(chǔ)能元件的電路中，電容和電感在吸收或釋放功率的是可以相互抵消的，無功功率之正負(fù)號的物理意義正在于此，即電容存儲(chǔ)的電能和電感存儲(chǔ)的磁能之間可以互相轉(zhuǎn)化。有的教材認(rèn)為，存在兩種儲(chǔ)能元件L和C的任何電路中，電容和電感在吸收或釋放功率的時(shí)間上正好相反[5]。由圖1(b)可知，上述說法是不準(zhǔn)確的，即電路中存在電阻元件時(shí)，電路中電容和電感在吸收或釋放功率的時(shí)間上并非正好相反。通過電路仿真軟件Multisim進(jìn)行仿真也驗(yàn)證了這一點(diǎn)。圖2所示的仿真是令圖1(b)中參數(shù)為R=5Ω、L=0.1H、C=2mF，激勵(lì)頻率為10Hz、有效值為1V時(shí)在0.7～1s內(nèi)電感和電容的瞬時(shí)功率曲線。由圖2可明顯看出兩種儲(chǔ)能元件功率的符號并非在所有時(shí)間內(nèi)正好相反。

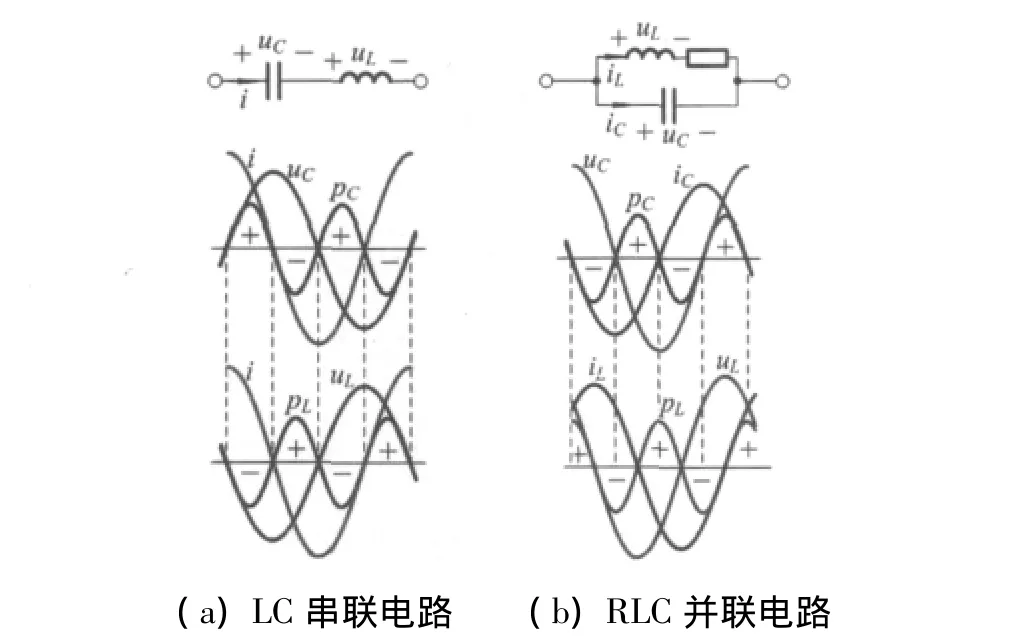
圖1 無功功率的正負(fù)號說明

圖2 圖1(b)的Multisim仿真結(jié)果

1.2 無功功率之大小的含義

在正弦穩(wěn)態(tài)時(shí)，儲(chǔ)能元件與外電路(電源)之間存在著能量不斷往返的現(xiàn)象。根據(jù)無功功率的定義，電感或電容的無功功率的大小反映了電感或的電容元件儲(chǔ)能變化率(瞬時(shí)功率)的最大值。進(jìn)一步，無功功率與儲(chǔ)能之間存在如下關(guān)系[1]:

請注意理解上式中各變量的含義(與教材[1]表示同)。由式(1)可進(jìn)一步理解無功功率的如下物理意義。

(1)電感的無功功率等于其儲(chǔ)能平均值WL的2ω倍;電容的無功功率等于其儲(chǔ)能平均值的WC2ω倍的負(fù)值。儲(chǔ)能越多，若能量往返的頻率越大則往返的規(guī)模也越大。無功功率能夠反映這一情況。

(2)由于平均儲(chǔ)能和頻率只能取正值，因此電感的無功功率永遠(yuǎn)是正值，而電容的無功功率永遠(yuǎn)是負(fù)值。

2 一般正弦穩(wěn)態(tài)電路的無功功率

2.1 無功功率的定義及物理意義

對于一般的正弦穩(wěn)態(tài)一端口電路，其端口電壓與端口電流的相位差φ=φu－φi。圖3所示為感性一端口電路的相量圖。

其實(shí)對于日常飲食來說，無論是白薯還是紅薯，都非常適合在日常三餐中經(jīng)常食用。含有豐富的膳食纖維和鉀元素、維生素C，也是它們共同的優(yōu)點(diǎn)。那么，怎樣吃甘薯才能更加健康呢？

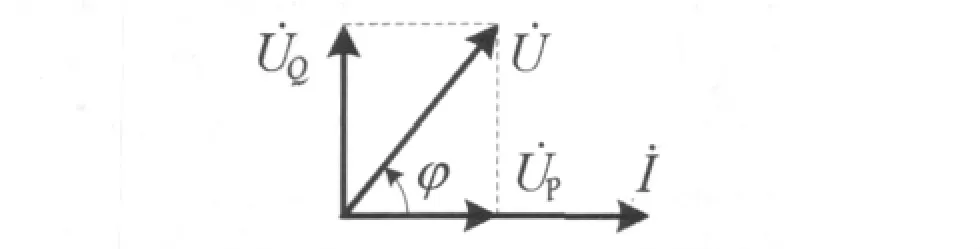
圖3 正弦穩(wěn)態(tài)一端口電路的相量圖

該一端口電路吸收的平均功率為

式中，UP=U cosφ。由相量圖可知，是與電流同相位的電壓分量，兩者有效值之積得到有功功率。因此U cosφ稱為電壓的有功分量或有功電壓。相量圖中的是與電流正交的電壓分量，兩者有效值之積得到無功功率，即

式中，UQ=Usinφ，稱為電壓的無功分量或無功電壓。

由上可知，對正弦穩(wěn)態(tài)電路，只要電壓和電流存在相位差就存在無功功率。無功功率還滿足如下關(guān)系:

上式表明:無功功率正比于電路中兩種平均儲(chǔ)能的差值。兩種儲(chǔ)能在電路內(nèi)部可自行交換，而與外電路往返的能量僅為兩種儲(chǔ)能平均值的差值。當(dāng)兩種儲(chǔ)能平均值正好相等，則電路與外電路(電源)之間并不存在能量往返的現(xiàn)象。因此，對一般正弦穩(wěn)態(tài)電路，其無功功率的大小同樣反映了外電路(電源)參與能量往返的程度。

由上面的討論可以看出:同相電壓、電流分量產(chǎn)生平均功率，而正交電壓、電流分量則產(chǎn)生無功功率。

由式(3)可知，一般正弦穩(wěn)態(tài)電路的無功功率是電感、電容元件無功功率定義的推廣。

2.2 無功功率與瞬時(shí)功率的關(guān)系

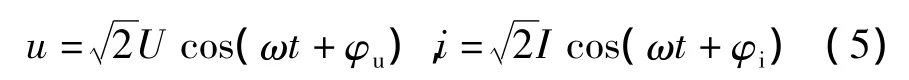
則該一端口電路吸收的瞬時(shí)功率為

圖4 正弦穩(wěn)態(tài)一端口電路

該功率是一個(gè)隨時(shí)間變化的量，為瞬時(shí)功率。瞬時(shí)功率p包括兩項(xiàng)，一項(xiàng)為常量，另一項(xiàng)為正弦量，頻率是電壓(電流)頻率的二倍。有的教材認(rèn)為上式右邊第一項(xiàng)為有功分量，第二項(xiàng)為無功分量[5]。這種說法比較模糊，它并不能解釋平均(有功)功率和無功功率的大小。

如何從瞬時(shí)功率中分解出有關(guān)分量和無功分量，應(yīng)注意理解“同相電壓、電流分量產(chǎn)生平均功率，而正交電壓、電流分量則產(chǎn)生無功功率”。可以證明，瞬時(shí)功率p亦可以表示為

可將上式右邊第一和第二項(xiàng)之和稱為有功分量PR，第三項(xiàng)稱為無功分量PX

事實(shí)上，可將圖4電路等效為圖5(a)所示的串聯(lián)模型。顯然有

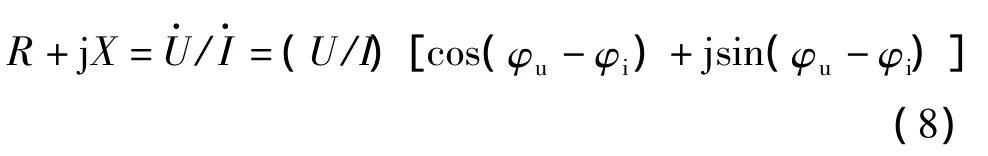
電阻分量的瞬時(shí)功率為

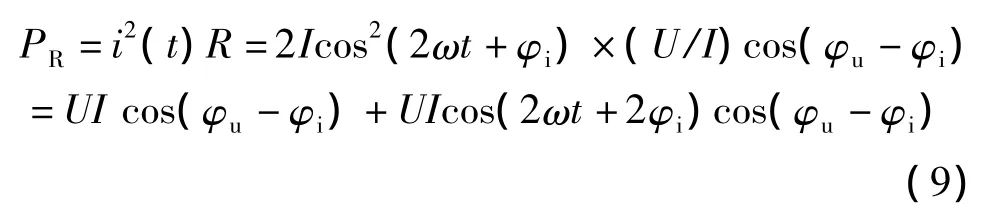
類似地，電抗分量的瞬時(shí)功率為

由式(7)不難得出平均(有功)功率為P=UIcos(φu－φi)，無功功率為 Q=UIsin(φu－φi))。注意，無功功率表達(dá)式前面取正號，這是因?yàn)榘凑諢o功功率的定義，規(guī)定電感的無功功率為正，電容的無功功率為負(fù)。

圖5 正弦穩(wěn)態(tài)一端口電路的兩種等效相量模型

圖4電路還可等效為圖5(b)所示的并聯(lián)模型。瞬時(shí)功率p還可以表示為與式(7)類似的公式:

上式右邊第一，第二項(xiàng)之和稱為有功分量RA，第三項(xiàng)稱為無功量PX。

同樣，由此可以得到平均功率和無功功率的正確表達(dá)式。

3 結(jié)語

本文針對電路教學(xué)中對無功功率理解上的一些問題進(jìn)行了討論，著重強(qiáng)調(diào)了如下幾點(diǎn)。

(1)平均功率是由同相電壓和電流分量產(chǎn)生的，而正交電壓和電流分量則產(chǎn)生無功功率。

(2)正弦穩(wěn)態(tài)電路的無功功率反映了網(wǎng)絡(luò)與外電路(電源)之間能量往返的規(guī)模。儲(chǔ)能越多，能量往返的頻率越大，則能量往返的規(guī)模也越大。

(3)無功功率可正可負(fù)，說明了電場儲(chǔ)能和磁場儲(chǔ)能在電路內(nèi)部可自行交換。這里必須特別指出的是，規(guī)定電感無功功率為正而電容無功功率為負(fù)，僅僅是為了公式表達(dá)和分析的方便。相反，如取電容無功功率為正而電感無功功率為負(fù)，則與無功功率相關(guān)的公式都應(yīng)作符號上的相應(yīng)修改。

(4)從穩(wěn)態(tài)電路的瞬時(shí)功率表達(dá)式中可分解出有功分量和無功分量，這兩個(gè)分量分別對應(yīng)平均功率和無功功率。值得指出的是，盡管本文給出了兩種不同的表示方法，但其本質(zhì)相同，兩種表達(dá)式的區(qū)別在于所取的時(shí)間起點(diǎn)不同。由式(7)和式(11)可以看出，兩者表達(dá)式在相位上相差φu－φi。

[1]李瀚蓀.簡明電路分析基礎(chǔ)[M].北京:高等教育出版社.2002

[2]陳洪亮，田社平，吳雪等.電路分析基礎(chǔ)[M].北京:清華大學(xué)出版社.2009

[3]陳希有.電路理論基礎(chǔ)[M].北京:高等教育出版社.2004

[4]吳大正.電路基礎(chǔ)[M].西安:西安電子科技大學(xué)出版社.2007

[5]吳錫龍.電路分析[M].北京:高等教育出版社.2004