內河船舶噸位丈量計算公式方法的討論

周社寧，褚衛明

(江蘇省船舶檢驗局，江蘇 南京 210004)

0 引言

《內河船舶法定檢驗技術規則》(2011)(簡稱“法規”)已于2011年9月1日開始實施，其中第3篇“噸位丈量”中對新造及有資料船舶計算量噸甲板下圍蔽處所容積V1做了較大的調整:將公式法改為容積計算方法。這一調整牽涉設計、審圖、檢驗和海事管理等諸多方面，特別對一些已按公式法習慣性做法或對此有既定管理規定(或軟件)的單位的船舶噸位計算工作影響較大，引起了不少爭議和討論。本文對公式法的由來及原理進行了介紹，分析了公式法存在的缺陷，從而得出用容積法代替公式法是必然趨勢。

1 公式法的由來及原理

1.1 公式法的由來

1959年我國參考英國、前蘇聯等國噸位丈量規則，以辛氏法作為基本點的“摩遜法”為基礎，制定了建國后的第1個《船舶噸位丈量規范》，適用于海船兼作河船參考，其內容比較簡單。1978年我國制定了第2個《船舶噸位丈量規范(國內航行船舶部分)》(試行本)，主要規定了包括辛氏法在內的3種容積丈量計算方法，其內容與1959年規范基本相同，只是要求更加詳細，增加了插圖和對船體凸出體的丈量方法，其適用范圍是海船河船通用。1986年我國發布了第一個明確為內河船適用的《內河船舶噸位丈量規范》，直至1999年、2004年、2011年的法規都將內河船舶噸位丈量與海船分開，單獨實施其計算方法。由于船舶噸位丈量歷來都有多種計算方法，比較繁瑣，根據當時我國內河船舶船型小、船型簡單、船舶噸位的社會作用不顯著、不敏感的特點以及計算機技術的落后，為簡化計算的工作量和避免結果的不一致，1986年的內河丈量規范統一采用了公式法的計算方法。該法相對于繁雜的手工計算而言比較簡單，結果相對準確，而且通常情況下對新造及現有資料船舶計算量噸甲板下圍蔽處所容積V1只允許使用此法。1986年至2011年一直沿用的公式法如下:

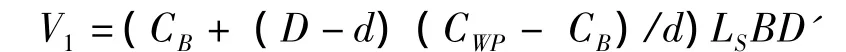
式中:d為設計滿載吃水;CB為設計滿載吃水時的方形系數;CWP為設計滿載吃水時的水線面系數;LS為設計滿載吃水時的水線長;B為型寬;D為型深;D′為修正型深，D′=D+h/2+(hS+hW)/6，其中:h為梁拱高;hS為船首舷弧高度;hW為船尾舷弧高度。

1.2 公式法的原理

1986年以前噸位丈量計算均采用排水體積式的容積曲線或邦氏曲線或辛氏法等方法求得V1的數值，而公式法則是采用了若干個相關船舶參數，通過這些參數的推算來求得V1的數值。公式法主要是使用CB值在靜水力曲線的外插及近似判斷和一定量船舶的統計數據分析的方法:公式中的D'取值為修正型深，這與排水體積的曲線計算方法無異;根據船舶參數的定義，公式中的V1也就是在D'下的型容積，(CB+(D－d)(CWP－CB)/d)就是在D'下的方型系數CB'，而(D－d)(CWP－ CB)/d就是對CB外插的修正值。

推導該公式的過程中，根據內河船舶特點，作了如下3個假設:

(1)設計水線以上水線寬保持不變，是個常數。

(2)水線面系數與吃水為線性關系，且在設計吃水一半時，水線面系數等于體積平均系數即方形系數。

(3)干舷不是特別高(1 m以內)。

公式中型深D'的修正計算含了梁拱和舷弧的影響，分別介紹如下:

(1)梁拱的影響

梁拱對主船體容積的影響，可以考慮為型深在原來基礎上的一個增加，如將梁拱線看成一直線，即原型深以上是三角形。根據等面積原理，與該三角形面積相等的矩形高應為梁拱高度的一半，即相當型深為:D′=D+h/2，此為2004法規中梁拱等效。如將梁拱線看成是一個弓形，根據等面積原理，與該三角形面積相等的矩形高應為梁拱高度的2/3，即相當型深為:D′=D+2h/3，此即為2011法規中梁拱等效。

(2)舷弧的影響

舷弧對主船體容積的影響與梁拱類似，但假定舷弧線看成是一拋物線，首舷弧的面積在前半體的等效高度為hS/3，綜合到全船范圍即hS/6，尾舷弧類似，相當型深為:D′=D+hS/6+hW/6

綜合梁拱、舷弧的影響為:

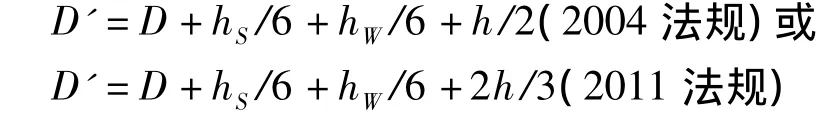
2 公式法的缺陷

(1)從上述推導公式看到，公式法是利用了CB與CWP隨吃水變化規律相似的特性，設置了一些假定，如設計水線以上水線寬保持不變或水線面系數與吃水為線性關系等，但實際上對絕大多數船舶而言這是不可能的。公式是在匯總了當時內河主流船型的基礎上統計得出的，忽略了它們的差異，因此不能以這些假設為前提的公式來涵蓋所有內河船舶。另外，為達到使假設或相似關系的成立及公式的簡化，在式中既有D的采用又有D′的引用，還有與這D與D′均無關的LS的引用，顯得比較混亂。這種D與D′位置差異及與LS的混用，對修正值CB′的準確確定無疑也是有影響的。

(2)從公式法中看出，CB的修正值(D－d)·(CWP－CB)/d中(D－d)/d愈大，則修正愈大，D的位置在d的外插位置，從數學上知道曲線斜率不等的情況下，外插點越遠外插的結果誤差越大。(D－d)/d表示的是干舷與吃水的比值，因此相對講船舶吃水愈淺，(D－d)/d就越大，外插誤差就越大，這就說公式法對淺吃水船噸位丈量計算產生的誤差大。而淺吃水船是內河中的典型船型，在內河船舶數量中占有相當的比例，使得公式法在淺吃水船中使用有很大的局限。

(3)從公式法中看出，(CWP－CB)值愈大，則修正值也愈大。對某一船來講由于船舶三維外型特性，(CWP－CB)值愈大或隨著吃水增加呈增長趨勢，則船舶外飄(包括側飄和前后飄)愈大，對這類船的噸位丈量計算產生的誤差一定也愈大。內河的客船、甲板貨船和一些其他船舶為追求較大的甲板面積，都存在著不同程度的外飄，有的還相當大，因此這類船使用公式法也有很大的局限。

(4)從公式法中看出，當時為使用簡便，對船舶附體和突出物的容積沒有考慮。隨著內河船型的大型化和復雜化，船舶帶有附體和突出物的現象愈來愈多，也使得公式法在使用中造成結果誤差增大。

在船舶噸位越來越受到社會關注的情況下，公式法的上述缺陷在使用過程中，對有些船的影響是單一的，對有些船是交織的，有些還是比較嚴重并且難以通過其他方法糾正或解決的缺陷。由于這些缺陷的綜合影響及不確定的作用，決定了其帶來的弊端還是較嚴重的。

如某1200客位渡船主要量度為:

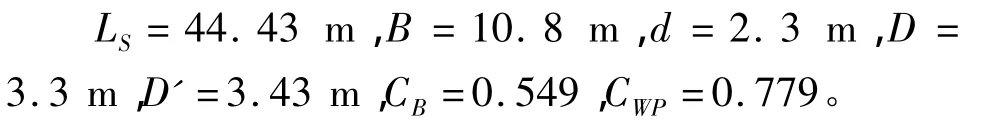
用公式法得到的V1=1009.6 m3;而用容積曲線方法得到的 V1=1107.5 m3，兩者相差 97.9 m3，換算成總噸，相差29。

某70 m散貨船主要量度為:

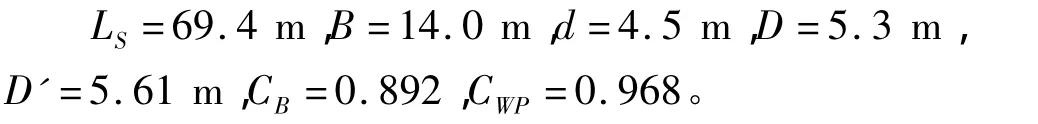
用公式法得到的V1=4938 m3;而用容積曲線方法得到的V1=4810 m3，兩者相差128 m3，換算成總噸，相差38。

3 公式法沿用與否的分析

從上述情況得知，1985年至2011年間內河船舶噸位丈量規范中對新造及現有資料船舶計算量噸甲板下圍蔽處所容積V1僅允許使用公式法顯然已不適宜，尤其在計算機和船舶軟件不斷發展的今天。通過計算機采用容積曲線方式進行噸位計算丈量，使得公式法已沒有任何優勢可言，特別是準確性方面更不如計算機計算結果精確。據不完全統計，采用公式法比容積曲線方法計算得到的V1結果平均誤差約在5%以內，折算成總噸的誤差在1% ～3%以內，因此不少人對公式法沿用與否產生了不同意見，包括新法規評審時也有爭議。其主要觀點為:

(1)有人提出既然公式法已沿用了20多年，經其丈量的船舶噸位也已經既成事實，況且噸位丈量僅是人為的約定行為，作為唯一的公式對同一種船型來講結果是公平的也是唯一的。

作者認為既然已經證明公式法存在缺陷，且這些缺陷不僅對船舶的共有屬性和總的公平帶來了影響，還對如設備配置、船員配備等產生延伸影響，特別是對一些臨界噸位的船舶的影響。問題越積越多，情況愈加復雜。與其長痛不如短痛，況且法規對現有船舶的噸位不做強制追溯;同時國際上通行的噸位丈量公約或規則的計算以及我國海船噸位丈量計算都是采用容積曲線或辛氏法，內河船舶在這方面沒必要作特殊的對待。

(2)有人提出公式法和容積曲線法能否共存，作為過渡期同時允許使用。

從上述的2個例子可以證明，2種方法假如同時使用，由于計算結果的差異，如果船東、設計單位或管理部門各取所需，將會給船舶噸位丈量工作帶來混亂，甚至成為社會問題。新法規在合理考慮過渡問題時已經注意到這個方面，即對無資料的現有船舶其主體部分和附加部分仍然允許采用公式法。由于目前這種無資料的現有船舶現象已很少，新法規這樣的方式既考慮到了以往的現實與過渡，也不會對今后新造船產生沖擊，是一種較宜的處理方法。

4 結語

用容積曲線方法或辛氏法代替公式法的趨勢是不言而喻的，《內河船舶法定檢驗技術規則》(2011)的這一調整是必要的，調整利大于弊，對此應該有一個明確的認識:公式法不能再應用于新造及現有資料船舶計算量噸甲板下圍蔽處所容積V1。至于對新內河法規中有關哪些項目是否應該計入噸位丈量的爭論，從而會引起我國內河船與海船、尤其與國際上的一些通常計入項目和其計算結果的偏差的問題，隨著時間的推移，大家也會有一個共識的。