隨機車輛荷載下三塔懸索橋鋼箱梁疲勞關鍵斷面分析

陳 策，吉伯海，劉 榮

(1.河海大學土木與交通學院，南京 210098;2.江蘇省長江公路大橋建設指揮部，江蘇泰州 225321)

1 前言

正交異性鋼橋面系統由頂板、縱肋、橫肋/橫隔板等構成，出現于20世紀50年代初期。正交異性鋼橋面板的整體性好、自重小，在大跨度鋼橋中有著廣泛的應用，已成為世界上大、中跨徑現代鋼橋通常采用的橋面結構形式。同時正交異性鋼橋面疲勞開裂的事例已在許多國家的鋼橋中出現，關于鋼橋面出現疲勞開裂，最早報道出現在英國 Severn橋，1966年建成通車后，分別于1971年和1977年發現了3種焊接細節的疲勞裂紋;德國的Haseltal橋和Sinntal橋投入使用后不久，鋼橋面板也都發現了疲勞裂紋。此外，日本、美國、荷蘭、法國等也都發現了鋼橋面板疲勞開裂事例。鋼橋面板在我國使用的時間雖然不長，但是已經在一些橋中發現了鋼橋面板的疲勞開裂［1～5］。這些實例表明，對鋼橋面板疲勞性能進行系統研究是非常必要的。

正交異性鋼橋面系統疲勞問題主要有以下幾個方面原因:a.鋼橋面板直接承受車輛輪荷載的反復作用;b.各部位應力影響線長度較短，一輛車經過可能會產生多個應力循環;c.鋼橋面板應力狀況比較復雜，并且交叉部位應力集中嚴重;d.U肋與橫隔板角焊縫以及許多現場拼接接頭的焊接質量不易保證;e.關于鋼橋面板構造細節的疲勞強度數據較少，各國規范對此還沒有明確規定。總體說來，正交異性鋼橋面系統的疲勞性能主要取決于正交異性鋼橋面頂板與U肋連接構造、正交異性鋼橋面頂板U肋與橫隔板連接構造兩方面，直接關系到橋面系的使用壽命和安全。

泰州大橋為千米級三塔懸索橋，其結構受力特點與傳統的雙塔懸索橋有較大的差異［6，7］。三塔懸索橋中塔兩側主跨箱梁受力相互影響，較雙塔懸索橋更為復雜，有必要對泰州大橋在車輛荷載作用下的主梁整體受力特點進行研究。

2 鋼箱梁疲勞應力分析

2.1 全橋三維有限元模型

泰州大橋雙主跨為1 080 m的三塔懸索橋，主梁為3.5 m高的鋼箱梁，全寬39.1 m，標準段長度為16 m。主纜矢跨比采用1/9，兩根主纜橫向中心距離為34.8m。主塔與主梁的結構關系為:中塔與主梁之間僅設置橫向抗風支座與縱向具有限位功能的彈性索，不設豎向支座;邊塔處主梁設豎向支座、縱向滑動支座與橫向抗風支座。

采用有限元軟件ANSYS建立泰州大橋全橋有限元模型，主梁與主塔均采用beam4梁單元進行模擬，通過將主梁、主塔截面CAD圖導入ANSYS中計算其截面的面積、慣性矩等參數。主纜與吊桿采用link10桿單元進行模擬，根據設計資料，將懸索與吊桿的設計索力換算為兩者的初應變，在計算中形成初應力剛度矩陣。主纜與吊桿連接處的索夾采用mass21質量單元進行模擬。全橋模型的邊界條件為:主纜兩端6個自由度全部約束，主塔底部6個自由度全部約束，主梁與主塔根據設計資料中約束關系采用主從耦合。圖1為泰州大橋的全橋有限元模型。為了模擬車輛荷載作為質量－彈簧模型在全橋結構上運行的過程，采用mass21質量單元模擬車輛重量，并通過combine14彈簧單元將質量單元與主梁進行連接。

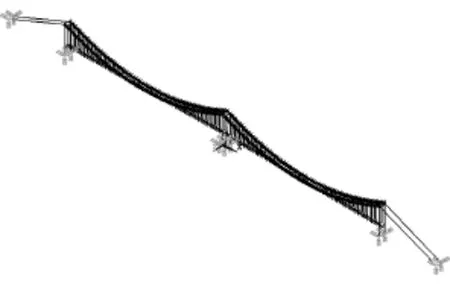
圖1 泰州大橋全橋有限元模型Fig.1 Global FEM model of Taizhou Bridge

2.2 疲勞車輛荷載譜模擬

車輛荷載作用下的疲勞損傷是不斷累積的過程，應采用實際的車輛作用歷程作為疲勞車輛荷載譜來計算橋梁構件的疲勞損傷。通過橋梁的車流狀態是一個隨機過程，其車型、軸重、車重及車輛間距等隨時間的變化而不同，但均服從一定的概率分布，通過Monte－Carlo法產生隨機數來模擬隨機車流。

基于對南京長江三橋、江陰長江大橋收費與稱重系統中海量數據的處理分析，得到兩座橋梁的隨機車流中車重及軸重兩個重要參數，將車型進行并歸分類，建立典型的車型庫，確定各車型所占比例，利用MATLAB統計工具箱抽取服從均勻分布的隨機樣本，將隨機樣本組合產生隨機車流(見圖2)，將隨機車流與疲勞車輛荷載模型結合，可以得到疲勞車輛荷載譜，可作為隨機車流下的泰州大橋整體振動的外部荷載。

2.3 車輛荷載的簡化模型

在車輛動力荷載的作用下，橋梁結構將產生振動、沖擊等動力效應。在實際工程中，確定車輛荷載的簡化計算模型是分析車載引起橋梁結構動力響應的關鍵之一。主要有三類簡化的車輛荷載模型即移動荷載模型、移動質量模型與移動車輛模型，文章選用移動質量模型。假定車輛模型由兩個質量組成，即剛度為Kv的彈簧支撐跳動質量Mvs和與橋梁始終保持接觸的不跳動質量Mvu，如圖3所示。車輛對橋梁的作用力可由式(1)表示，式(1)中，Z為彈簧質量Mvs的絕對位移，由中性位置計算。yv為彈簧質量Mvu與橋梁結構的位移。若僅考慮一階振型，則有振型方程與彈簧上質量動力平衡方程可由式(2)、式(3)表示，式中，CB與Cv分別為橋梁與車輛系統的阻尼系數。

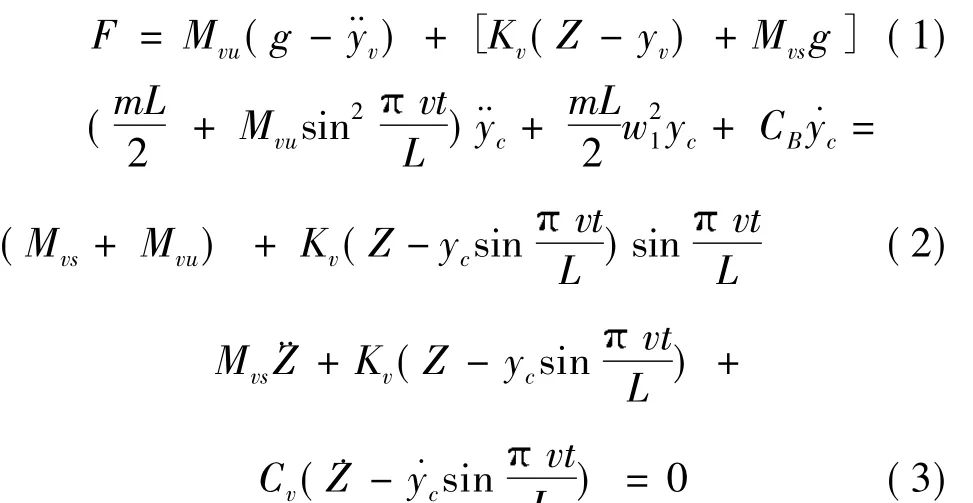
移動質量模型考慮了車輛的剛度、慣性力對橋梁結構的影響，通過在有限元中對車輛的質量及剛度進行模擬便可以實現，有利于實際工程中的運用，且影響因素考慮得相對全面。

2.4 動力響應分析

在車輛荷載作用下，主梁各部位將產生不同程度的振動響應。為了確定泰州大橋鋼箱梁節段在隨機車流荷載作用下應力變化敏感的位置，對主梁的位移與內力動力響應進行了研究。采用隨機車流對泰州大橋全橋模型進行振動分析。計算車速采用設計車速80 km/h。

2.4.1 主梁位移動力響應

在隨機車流作用下提取鋼主梁左側、右側跨中、1/4跨、3/4跨處的位移響應，計算時程為3 min。計算結果表明，鋼箱梁各截面處的豎向位移靜力響應由若干個大的位移循環組成，豎向位移動力響應曲線變化趨勢基本與靜力響應曲線相同，且都圍繞靜力響應曲線小幅波動。當隨機車流集中在一跨時，該跨的豎向位移響應增加明顯，另一跨鋼主梁向上翹曲，豎向位移響應減小，兩跨間的位移響應相互影響。同時，在隨機車流作用下，泰州大橋主梁左右兩側跨中的最大豎向位移分別為1.56 m、1.55 m，位移值接近。左右兩側1/4跨的最大豎向位移分別為1.42 m、0.77 m，左右兩側3/4跨的最大豎向位移分別為0.79 m、1.39 m，兩側鋼箱梁在對應截面位置處的豎向位移值的差異主要是由于中塔對主梁的約束不同而引起的。

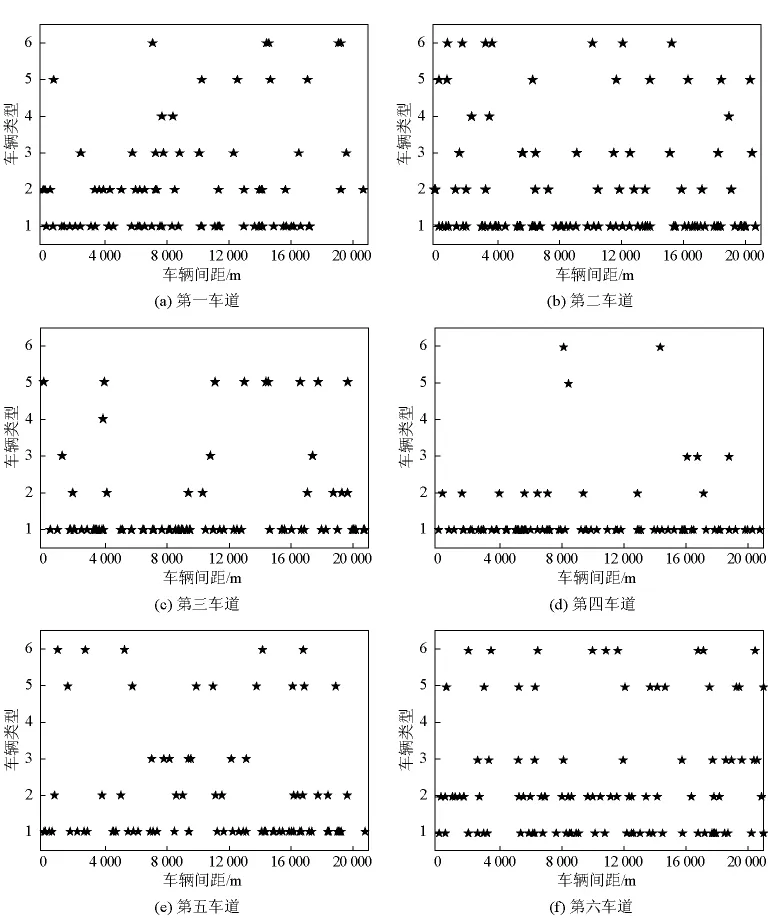
圖2 江陰大橋各車道隨機車流Fig.2 Random vehicle load at different driveways of Jiangyin Bridge

圖3 車輛荷載移動質量模型Fig.3 Mobile quality model of vehicle load

2.4.2 主梁內力動力響應

圖4為鋼箱梁在對稱車流作用下的彎矩響應，圖中分別為左、右側跨中、1/4跨、3/4跨處的主梁彎矩動力、靜力響應。

計算結果表明，車流荷載作用下大橋主梁不同部位內力振動響應曲線總體波動趨勢與靜力響應曲線相似，彎矩動力響應圍繞靜力響應小幅波動。主梁左、右兩側的跨中位置的彎矩最大變化幅值分別為(6.19E+07)N·m、(7.45E+07)N·m。左、右側1/4跨處的彎矩最大變化幅值分別為(4.87E+07)N·m、(7.19E+07)N·m。左、右側3/4跨處的彎矩最大變化幅值分別為(5.80E+07)N·m、(6.49 E+07 N)·m。鋼箱梁的彎矩變化是影響其應力幅的主要因素之一，以彎矩時程作為評價標準，兩主跨跨中截面的疲勞受力為最不利。

3 結語

根據南京長江三橋及江陰長江大橋的實測車輛荷載數據，產生隨機車流，與疲勞車輛荷載模型結合，得到疲勞車輛荷載譜作為泰州大橋整體振動的外部荷載。采用移動質量模型，將隨機車流加載于全橋有限元模型上，計算泰州大橋主梁不同位置處豎向位移和彎矩的振動響應值。研究結果表明，車輛荷載下，兩主跨跨中截面的疲勞受力為最不利。

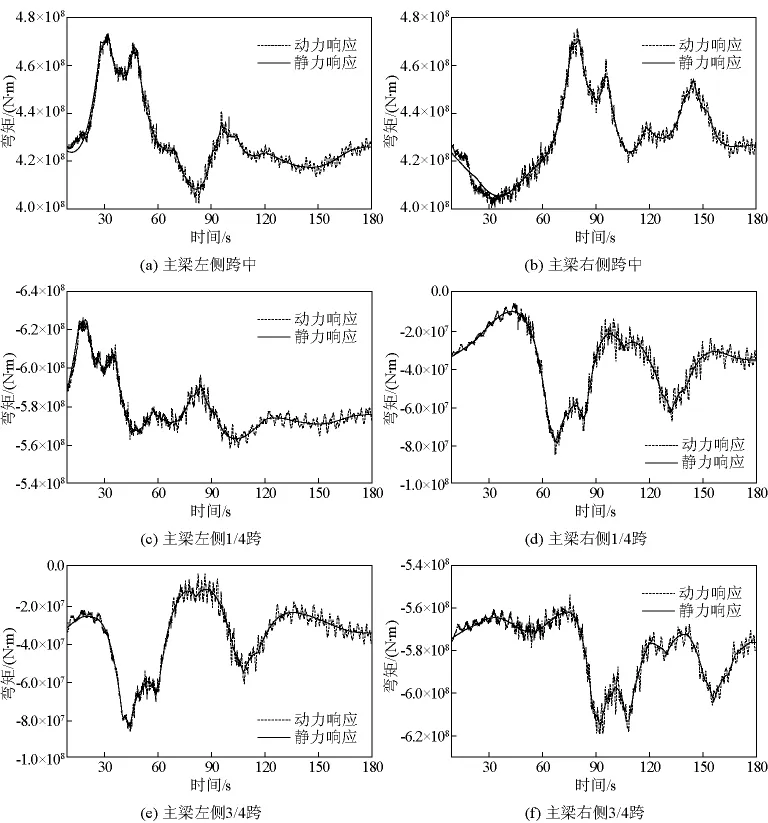
圖4 對稱荷載作用下主梁彎矩響應Fig.4 Bending moment response of main girder under symmetrical load

［1］Roman Wolchuk.Lessons from weld cracks in orthtropic decks on three European Bridges［J］.ASCE，1990，116(1):75 －84.

［2］黃 衛.潤揚長江公路大橋建設第五冊:鋼橋面鋪裝［M］.北京:人民交通出版社，2005.

［3］陳惟珍，童樂為.公路鋼橋疲勞與防斷裂設計理論與方法研究［G］.上海:同濟大學橋梁工程系，2006.

［4］吳 沖.現代鋼橋［M］.北京:人民交通出版社，2006.

［5］項海帆.高等橋梁結構理論［M］.北京:人民交通出版社，2002.

［6］陳 策.大跨徑三塔懸索橋抗風性能分析［J］.鐵道標準設計，2008(2):30－33.

［7］陳 策，鐘建馳.三塔懸索橋垂跨比變化對結構靜動力特性的影響［J］.橋梁建設，2008(6):12－14.