離散點集最小包圍圓算法分析與改進

李紅軍 ， 張曉鵬

（1. 北京林業大學理學院，北京 100083；2. 中國科學院自動化研究所模式識別國家重點實驗室&中法聯合實驗室，北京 100190）

平面點集的最小包圍圓(smallest enclosing disk)問題的提出至少可以追溯至1857年[1]。只是隨著計算機技術的快速發展，點集的最小包圍圓應用越來越廣泛，比如在工業機器人的設計、碰撞檢測、機器學習、計算機圖形學等領域中都有應用，研究成果也越來越多。僅就這個問題的算法設計而言，國內外也有不少文獻。本文對這些現有的典型算法給予簡單的介紹并進行分析和比較。為了避免重述，早期的研究結果可以參考Emo Welzl的有關工作[2]。1991年，Welzl在這篇文章中對早期的一些研究方法和結果進行了簡要評述并提出了新方法。Welzl用隨機增量算法求解平面點集的最小包圍圓或橢圓( smallest enclosing ellipse )，并把這個算法推廣到高維空間的最小包圍球(smallest enclosing ball )、最小包圍橢球(smallest enclosing ellipsoid )。后來的Mark de Berg等作了進一步的改進[3]，我們稱之為改進的隨機增量算法。2005年，Frank Nielsen等也提出了一個基于對偶決策的、快速的、確定性算法[1]，這里稱之為對偶決策算法。2000年復旦大學汪衛等提出了一個離散點集最小包圍圓的快速算法，我們稱之為最遠點優先漸近算法[4]。這3種算法思路清晰，不失為有代表性的經典算法。本文將對這3種算法進行分析、比較。

1 離散點集最小包圍圓和典型算法

1.1 最小包圍圓問題

問題：對于給定的平面上n個點所組成的一個集合P，求出P的最小包圍圓，即包含P中所有點、半徑最小的那個圓。也就是求出這個最小包圍圓的圓心位置和半徑。

對于這樣的問題，為了便于理解各種算法，需要了解一些有關最小包圍圓的性質：

性質 1 有限點集P的最小包圍圓是唯一的。

這里約定，若P中只有一個點v，則最小包圍圓是退化的，其半徑為 0，圓心為點v。這個定理的詳細證明參見文獻[2]。

性質 2 非退化最小包圍圓可以由 2個或者3個邊界點定義。

顯然，最小包圍圓的構成有兩種情況：第1種是距離最遠的2個邊界點定義了最小包圍圓的直徑。如圖 1(a)所示，直徑AB定義了這個最小包圍圓，其余的點都是包含在這個圓的內部。這意味著不能僅僅通過求最大三角形的外接圓來計算最小包圍圓。第2種情況是最小包圍圓的邊界上有3個以上的點，則任意3個邊界點為三角形頂點所定義的外接圓確定了這個點集的最小包圍圓。如圖 1(b) 所示，這個最小包圍圓由邊界點 A、B、C所形成的三角形的外接圓定義。需要注意的是，邊界線上可以有3個以上的點，只是任意3個邊界點定義的外接圓是相同的。因此，求點集P的最小包圍圓等價于求這些邊界點的最小包圍圓。

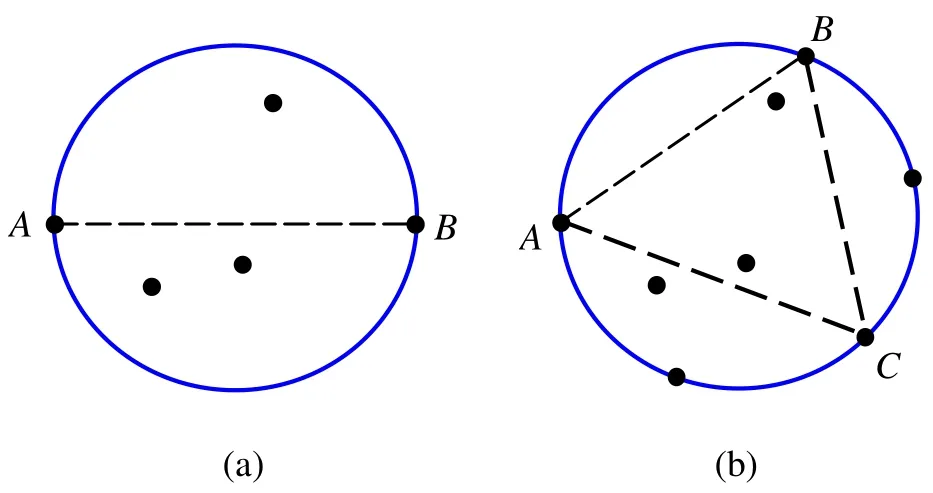
圖1 最小包圍圓由2個或3個邊界點確定

性質 3 點集P中，距離最大的2個點A、B不一定都在邊界上，但是必有，這里d為點集P的最小包圍圓的長度。

如圖2所示，點集P的最小包圍圓由等邊三角形ABC所定義，但是線段AD卻是最大的邊。顯然，線段AD為直徑的圓小于點集P的最小包圍圓。

證明見文獻[3]。

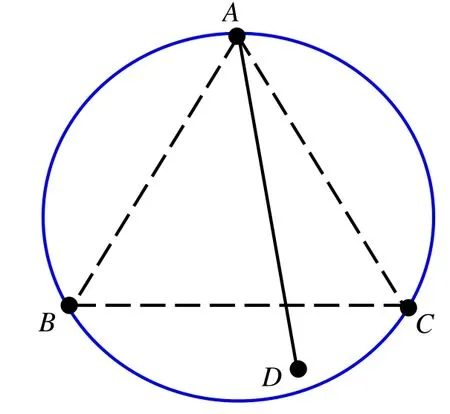
圖2 最長線段不一定是最小包圍圓直徑

性質 4 直角三角形或鈍角三角形的3個頂點的最小包圍圓是以最長邊為直徑的圓；銳角三角形3個頂點的最小包圍圓是三角形的外接圓。

證明：（1）設直角三角形或鈍角三角形ABC的最大邊為AB，則A、B兩點確定的最小包圍圓是以AB為直徑的圓，則點C在圓上或者圓內，如圖3(a)所示。根據引理1的前一部分知，A、B、C 3點確定的最小包圍圓還是以AB為直徑的圓。

（2）對于銳角三角形ABC，由于點C不屬于以AB為直徑的圓，因此，根據引理1的后一部分知點C在A、B、C三點確定的最小包圍圓DABC的邊界上；同理B和C也在最小包圍圓DABC的邊界上。不共線3點確定1個圓，所以DABC是A、B、C的外接圓，見圖3(b)。

上述性質對于理解、構造或者實現最小包圍圓算法有一定幫助。下面對幾個常用的、經典的算法思想進行簡要介紹和分析。

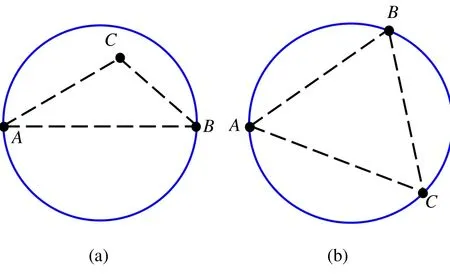
圖3 不共線三點確定的最小包圍圓

1.2 改進的隨機增量算法

Mark de Berg曾給出一種比較典型易于理解的隨機增量算法(randomized incremental algorithm, 簡記為 RIA)[3]。 其主要思想是：第一，隨機打亂點集中所有點的順序；第二，以序列中前2個點構造最小包圍圓D；第三，依次搜索其余的點，若某個點v在D外，則重新構造最小包圍圓D'，使D'飽含D中的所有點且以v為邊界點。重復執行第3步，直到求出最小包圍圓。

這個算法的關鍵在于第3步，以v作為邊界點構造最小包圍圓，從而增加了構造約束，減少了自由度。該算法的內存耗用少，速度快。在隨機點集的條件下，期望運行時間為O(n)。但是，若原始輸入序列是有序的，則打亂點集的順序也是需要耗費時間的。

1.3 最遠點優先漸近算法

2000年汪衛等提出一種準確且快速的點集最小包圍圓算法[4]，即最遠點優先漸近算法，簡記為DFAA。該算法的主要步驟是：第一，在點集中任取3個點:A、B、C；第二，以這3個點構造最小包圍圓D；第三，在點集P中查詢距離D的圓心最遠的點v；若v在D內則算法終止；否則，第四，在{A，B，C，v}中選取3個點，構造包含這4個點的最小包圍圓D'，轉第二步驟，其中選取的這3個點盡可能是邊界上的點。

該算法實際上是一個確定性算法。主要的困難和時間耗費在第四步。事實上，根據引理1，這一步是可以改進的，因為新加入的點v必定是新的最小圓的邊界點。于是這一步可以修改為：

以 v為邊界點，并在{ A，B，C }中選取 2個點，構造包含這4個點的最小包圍圓D'，轉第二步驟，其中選取的這3個點盡可能是邊界上的點。

修改后的算法判斷會減少，從而加快運行時間。第 3節的數值實驗以修改后的算法（記為DFAA+）作為對比。該算法的時間復雜度為中R是所求的最小圓的半徑，d為點集中不在圓周上但距圓周最近的點到圓周的距離。實際應用中，該算法時間復雜度是線性級的。

1.4 對偶決策算法

2005年Frank Nielsen提出一個快速近似的最小包圍圓算法[1]，這個算法通過求解一系列的對偶決策問題(dual piercing Decision Problems)來實現，簡記為DPs。該算法的主要思想是：第一，計算所有點在x軸上的投影區間[min x, max x]；第二，計算所有點到第1個點的距離最大值d1；第三，以4為初始半徑，以 ε =8為誤差控制，搜索區間為[maxx- r, minx+r]構造對偶決策，并進行迭代求解。其中，ε0為用戶指定的誤差控制閾值。

該算法優點是不但能夠求出平面上點集的最小包圍圓，也能求出圓盤集的最小包圍圓。算法時間復雜度為，其中ε為最小包圍圓的誤差控制閾值，即該算法是一個近似算法。該算法的速度較快，也屬于線性階的，此外，算法基本屬于確定性算法，其最壞時間復雜性比平均時間復雜性略差。但是該算法設計比較復雜，內存耗用比上述兩種算法大。

上面這3個常用算法以隨機增量算法影響比較大，我們的算法主要是對這個隨機增量算法進行改進，使其成為確定性算法，并加快求解時間。

2 較遠點對定義初始包圍圓的增量算法

文獻[3]介紹的隨機增量算法試圖通過生成點集的隨機順序來避免最壞時間復雜性，從而優化求解過程。事實上，這個目的可以通過調整距離較遠的 2個點作為輸入的前 2個點而得以解決。之所以不用相距最遠的2個點，是因為求解相距最遠的點對比較耗時。我們改進算法的主要步驟是：

Step 1 計算點集P的軸定向包圍盒，并記錄分別屬于不同邊的4個邊界點，設為,，如圖4所示。軸定向包圍盒的邊界點或許超過4個，為了減少算法比較和內存耗用，每條邊記錄1個邊界點。

圖4 計算點集的包圍盒信息

Step 2 計算這個軸定向包圍盒的寬(Bw)和高(Bh)。

Step 4 構造包含p1,p2的最小圓。之后的步驟用第1.2節介紹的改進的隨機增量算法。

根據性質3易知，p1,p2確定的最小包圍圓是整個點集的最小包圍圓的子集。從這 4步 可以看出，本文的改進算法是對改進的隨機增量算法的初始包圍圓進行了特定的初始化，使得初始包圍圓比較大，而計算這種軸定向包圍盒的時間復雜度是O(n)的，因而迭代次數減少，計算時間減少。更重要的是，這樣可以避免點集的最壞輸入順序，也不需要對輸入點集生成隨機順序。我們把這個算法稱為較遠點對定義初始包圍圓的增量算法, 簡記為FIIA。

3 實 驗

數值驗證實驗是在個人臺式電腦上進行。電腦的主要配置是：Intel(R) Core(TM)2 Extreme,CPU X9650@3.0GHz, 內存為3.0G。

為了對比本文分析的3個經典算法和本文的改進算法，設計了4組數據：矩形域隨機點集、圓域隨機點集、共線隨機點集和共線有序點集。其中，前2個數據為二維區域隨機點集。

矩形域隨機點集的采樣區域為

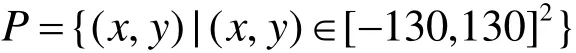
采樣點選取為此區域內的服從均勻分布的隨機數對。

圓域的隨機點集采樣區域為

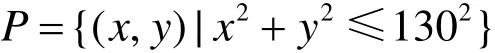
共線隨機點集和共線有序點集都是來自于直線上的點，直線方程為

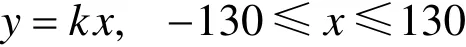
其中，本次實驗的參數k=0.4。這2個點集的差別在于共線隨機點集的點序是隨機的，而共線有序點集是按照x坐標遞增采樣。相鄰2個采樣點之間的間隔引入隨機數。這4個數據的采樣點個數和求取最小包圍圓的平均實驗時間列在表1。其中平均實驗時間為實驗重復進行 50次的平均運行時間。表1中的RIA表示改進的隨機增量算法(見第1.2節)， DFAA+為改進第四步后的最遠點優先漸進算法(見第1.3節)，DPs表示對偶決策近似算法(見第1.4節)， FIIA為本文提出的較遠點對定義初始包圍圓的增量算法(見第2節)。表

1中各個數據的最優時間用加粗的字表示。從表1可以看出，在本文羅列的3種經典算法中，在對偶決策近似算法(DPs)時間開銷最大。最遠點優先漸進算法(DFAA+)最好。本文較遠點對定義初始包圍圓的增量算法(FIIA)是對隨機增量算法(RIA)的改進，時間效率大大提高，尤其是點集為共線的情況下，效果更加顯著。

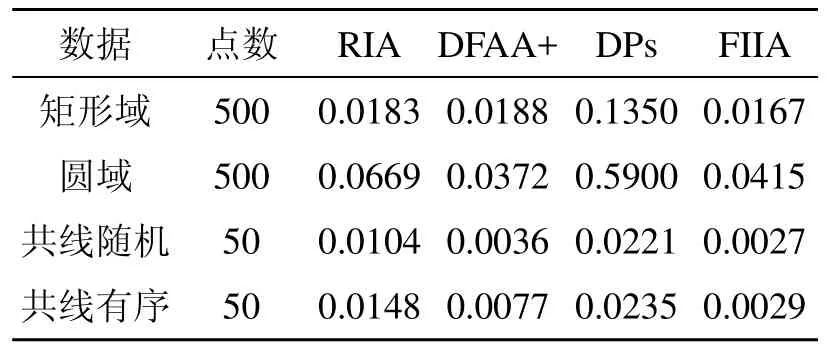
表1 實驗數據信息和平均運行時間

實驗數據的截圖如圖5所示，因為4個算法算出的圓心和半徑相同，故實驗結果的截圖相同，因而也說明各個算法的正確性。

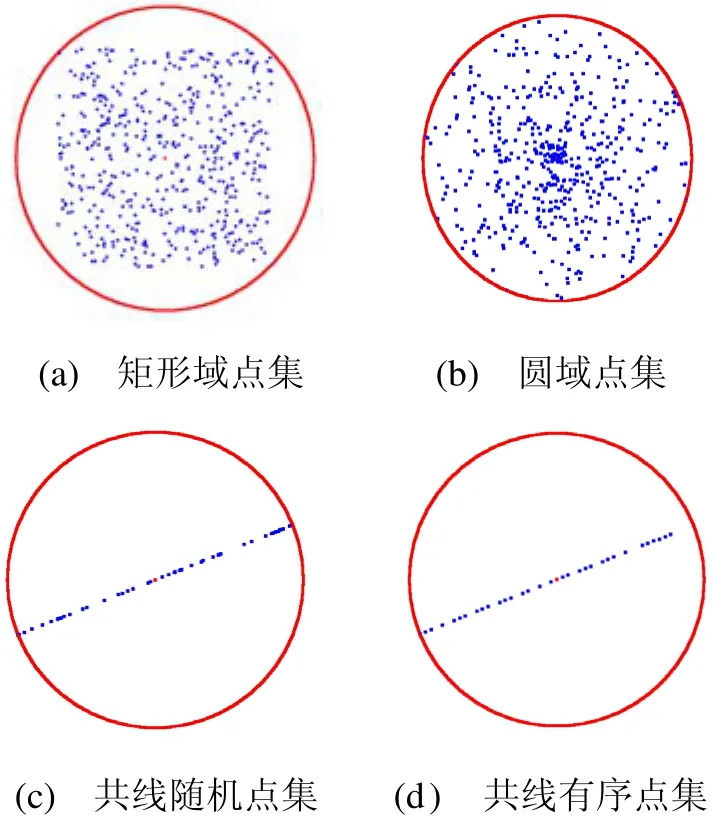
圖5 實驗數據及其最小包圍圓

實驗中最小包圍圓的空間擴展過程也可以顯示不同方法的收斂速度。這里我們把RIA算法和我們的FIIA算法進行對比，如圖6所示。圖6中的實驗包含 50個隨機點，每個子圖下方的數字表示前k個點確定的最小包圍圓。圖6中的第1行3個圖顯示RIA算法的最小包圍圓的動態擴展過程，第2行是我們的FIIA算法的運行結果。

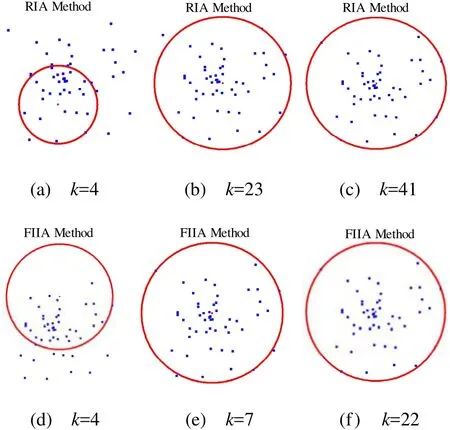
圖6 RIA和FIIA算法前k個點確定的最小包圍圓, (a)-(c)為RIA算法結果；(d)-(e)為FIIA算法結果。

對比2行的k值可以看出，RIA算法在前41個點時可以求得最小包圍圓。而我們的 FIIA算法，由于預處理中選取了距離較大的2個點作為前2個輸入點，因此收斂速度快很多，算法在計算到前 22個點時就求得了最小包圍圓。可見，我們的改進算法在收斂速度方面有明顯的優勢。

4 結 論

關于離散點集的最小包圍圓問題，本文首先概述了點集最小包圍圓的幾個主要性質，這對于理解或構造最小包圍圓算法有直接的影響。接著本文對隨機增量算法、最遠點優先漸近算法、對偶決策算法等當前比較常用、比較典型的算法進行分析和對比實驗，結果表明過去的這3種算法中，汪衛等 2000年構造的最遠點優先漸近算法在時間效率方面最高。其間我們對最遠點優先漸近算法進行了細微的改進，減少了枚舉次數。

本文主要對隨機增量算法改進，即用軸定向包圍盒邊界上的較遠點對，作為隨機點集序列的前兩個元素，實現隨機增量算法的輸入點順序的優化。基于這一改進，本文提出的這個算法稱為較遠點對定義初始包圍圓的增量算法(FIIA)。我們的這個新算法是確定性算法，不再需要對點集的順序進行隨機化處理，并且求取最小包圍圓的速度顯著提高。在工程實踐中，點集的軸向包圍盒往往在讀入數據時就已經算好，因此，其結果能直接取代本算法的前兩步驟而獲得更好的時間性能。

[1]Frank N, Richard N. A fast deterministic smallest enclosing disk approximation algorithm [J].Information Processing Letters, 2005, 93(6): 263-268.

[2]Emo W. Smallest enclosing disks (balls and ellipsoids)[C]// Maurer H. (Ed.), New Results and New Trends in Computer Science, Lecture Notes in Computer Science, Heidelberg: Springer-Verlag,1991: 359-37.

[3][荷蘭]Mark de Berg, Marc van Kreveld, Mark Overmars, et al. 計算幾何: 算法與應用(第2版)[M].鄧俊輝譯. 北京: 清華大學出版社, 2005: 99-103.

[4]汪 衛, 王文平, 汪嘉業. 求一個包含點集所有點的最小圓的算法[J]. 軟件學報, 2000, 11(9):1237-1240.