基于C-B樣條的三角形和四邊形曲面生成

李 薇， 吳卓奇， 荻原一郎

（1.南京信息工程大學數理學院，江蘇 南京 210044；2.上海交通大學機械與動力工程學院，上海 200240；3.東京工業大學理工學研究科，日本 東京 152-8550）

自由曲面在計算機輔助設計(CAD)及幾何模 型等領域有著重要和廣泛的應用。我們知道，B樣條和有理B樣條已經成為自由曲線曲面表示的標準，具有參數曲面表示和精確表示圓錐曲面等優點,但是由于其多項式及有理多項式的表示形式會產生一些局限性，例如，它在張量積的拓撲方面的限制是一個很大的缺點，往往會為了滿足數據網格的拓撲結構而增加多余的控制點，從而給幾何造型增加了難度。其有理多項式的表示形式，求導求積分復雜繁瑣，而且微分后分母的階數過高，給討論其連續拼接時增加了困難。另外有理 B樣條中的每個控制點都有的權因子的確定方法也不明確，再就是它也不能精確的表示像螺旋線，擺線等一些超越函數曲線[1]。

為了克服上述問題，ZhangJiwen[2-4]和Pottmann[5]分別考慮了由基底{sin t, cos t, t, 1}產生的C-B樣條曲線。由C-B樣條曲線可以構造張量積型曲面[4]，我們在這篇文章中利用邊-頂點方法[6]構造插值算子, 再將這些算子進行凸性組合[7-9]，分別將 C-B樣條曲線推廣成三角形曲面片和四邊形曲面片，它可以用于CAD的逆向工程的測量數據網格的曲面重建。

1 預備知識

C曲線由基底函數{sin t, cos t, t, 1}生成，它不僅可以精確表示二次曲線，還可以表示工程中用到的螺旋線，擺線等一些超越函數曲線。C曲線和三次曲線具有類似的結構與性質，也有三種曲線形式，分別叫做C-Hermite多項式，C- Bézier曲線及 C-B樣條曲線。這里，我們只介紹 C-B樣條曲線，其他2種曲線生成曲面的方法類似。

C-B樣條曲線在區間(0,)α(α≤π)的定義為

下面介紹重心坐標[10]：

設T 是三維空間3個點T1，T2，T3為頂點的一個三角形，P為這個三角形所在平面上的一點，P可以表示為

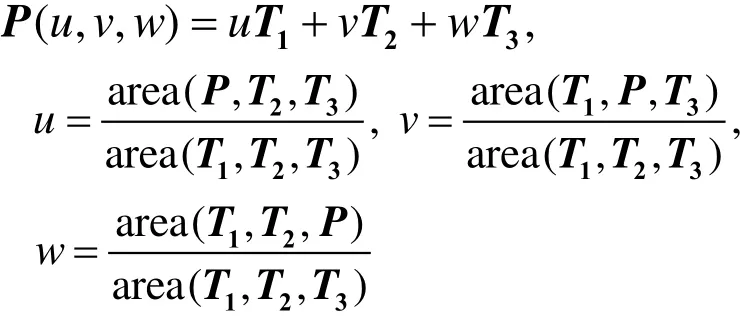
這里，u+v+w=1，u, v, w 叫做點P關于三角形T的重心坐標。

2 三角形曲面的生成方法

首先，利用邊-頂點方法構造3個插值算子

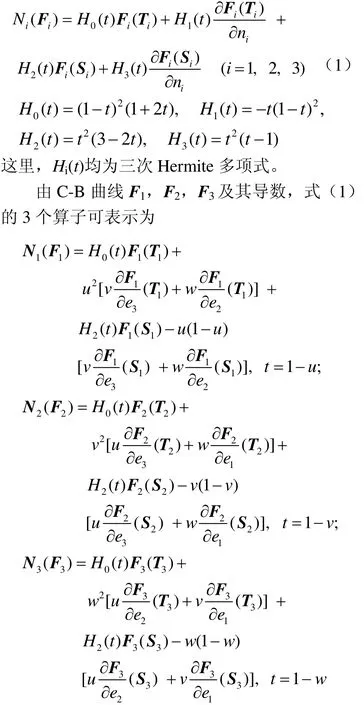
將這3個算子進行凸性組合得到三角形曲面片如下

這里u, v, w 是重心坐標。根據上式，3個算子插值于邊界曲線 F1，F2，F3及其一階導數，所構造的曲面片內部是C1連續的。

若將式(2)中 3個算子的系數權函數表示為W1,W2,W3, 即

圖1顯示了三角形區域的邊界上的3條C-B曲線F1，F2，F3，圖2給出了由這3條C-B曲線所生成的三角形曲面。

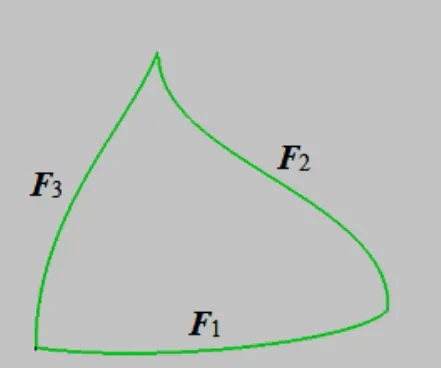
圖1 邊界上的3條C-B曲線

圖2 由邊界上3條C-B曲線生成的三角形曲面

3 四邊形曲面的生成方法

為了在定義域為四邊形的區域上生成四邊形曲面，類似三角形曲面的生成方法，首先利用邊界上的4條C-B曲線F1，F2，F3，F4，構造2個插值于邊界曲線 F1，F2，F3，F4及其一階導數的算子

下面的圖3及圖4顯示了上述方法的實驗結果。

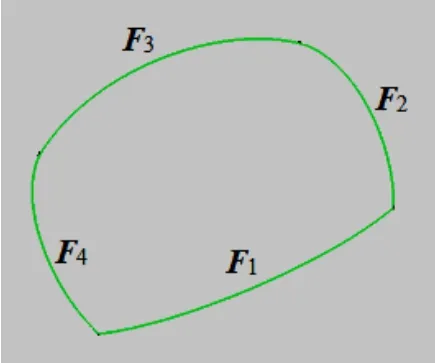
圖3 四邊形區域邊界上的4條C-B曲線

圖4 邊界上的4條C-B曲線生成的四邊形曲面

4 實驗結果及結論

上述所構造的曲面片可以用于CAD逆向工程。例如，用激光掃描或三維 CCD照相機可以得到幾何實體的一組測量數據，將其網格化后，形成三角形或四邊形網格，然后在這些網格上生成光滑的復合曲面。

例1 一個狗的測量數據由640個點及1286個三角形組成如圖5所示，生成的復合曲面顯示于圖6。

圖5 狗的三角形網格

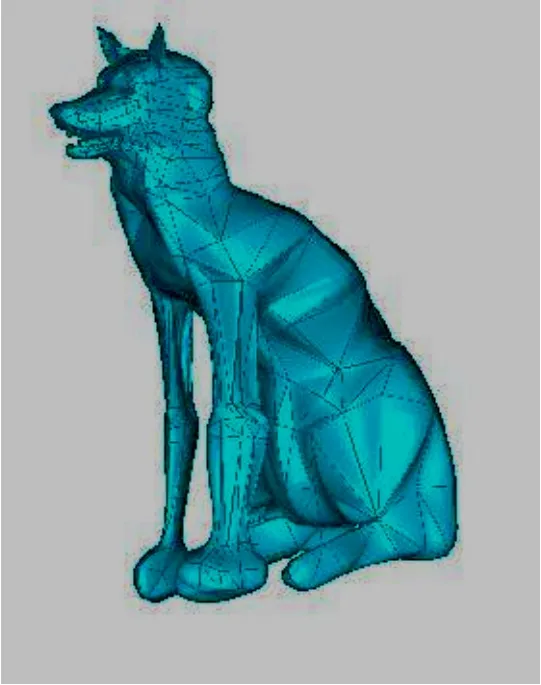
圖6 由狗的網格生成的曲面

例2 這是一組由三角形和四邊形混合組成的網格（圖7）生成的復合曲面（圖8）。

圖7 三角形和四邊形混合組成的網格

圖8 由混合網格生成的曲面

本文給出了將 C-B樣條曲線推廣成三角形和四邊形曲面片的方法。利用邊-頂點方法構造插值算子，再將這些算子進行凸性組合，可以構造內部C1連續的三角形曲面片和四邊形曲面片，通過實例驗證了它可以用于CAD的逆向工程中散亂數據的曲面重構。從實驗結果，其保凸性、恢復形狀及內部光滑性較好，但目前無法像伯恩斯坦多項式為基底的三角形曲面在曲面內部有控制點可以進行曲面形狀的調整，這是今后需努力的方向。另外今后還將探討所構造的三角形曲面片和四邊形曲面片之間的光滑拼接條件和方法。

[1]Mainar E, Pe?a J M and Sánchez-Reyes J, Shape preserving alternatives to the rational Bézier model [J].Computer Aided Geometric Design, 2001, 18(1):37-60.

[2]Zhang Jiwen. C-curves: An extension of cubic curves [J].Computer Aided Geometric Design, 1996, 13(3):199-217.

[3]Zhang Jiwen. Two different forms of C-B-splines [J].Computer Aided Geometric Design, 1997, 14(1):31-41.

[4]Zhang Jiwen. C-Bézier curves and surfaces [J].Graphical Models and Image Processing, 1999, 61:2-15.

[5]Pottmann H, Wagner M G. Helix splines as an example of affine Tchebycheffian splines [J].Advances in Computational Mathematics, 1994, (2):123-142.

[6]Nielson G M. The side-vertex method for interpolation in triangles [J]. Journal of Approximation Theory,1979, 25: 318-336.

[7]Gregory J A. N-sided surface patches [C]//Gregory J.(Ed.), The Mathematics of Surfaces. Clarendon Press,Oxford, 1986: 217-232.

[8]Hagen H. Geometric surface patches without twist constraints [J]. Computer Aided Geometric Design,1986, 3(3): 179-184.

[9]Hagen H, Pottmann H. Curvature continuous triangular interpolants [C]//Lyche T, Schumaker L L. (Eds.),Mathematical Methods in Computer Aided Geometric Design, Academic Press, New York, 1989: 373-384.

[10]Farin G. Curves and surfaces for computer aided geometric design —— a practical guide [M]. Second Edition, Academic Press, 1990: 217-222.