永磁同步電動機調速系統的離散滑模控制

楊朋松，孫秀霞，董文瀚，孫 彪，趙云雨

(1.空軍工程大學，陜西西安710038;2.94136部隊，寧夏銀川750000)

0 引 言

由于以永磁同步電動機(以下簡稱PMSM)為執行部件的高性能調速系統容易受系統參數變化和外界干擾的影響，因此難以采用PID方法實現滿意的調速和定位性能［1］。滑模變結構控制是一種魯棒控制方法，它的滑動模態物理實現簡單，且使系統在受到攝動及外干擾時均具有不變性［2］。滑模變結構控制理論在PMSM控制系統中的應用引起了人們的廣泛關注，并取得了不少研究成果［3－6］。

隨著計算機控制技術和PMSM在工業領域的廣泛應用，研究離散滑模控制技術及其在PMSM中的應用顯得極其必要。然而，離散滑模控制技術在PMSM控制系統中的應用研究相對較少。文獻［7］設計基于內模控制和離散時間趨近律控制的PMSM傳動系統，消弱了系統性能對電機模型精度的敏感性，達到了較好的傳動性能。文獻［8］提出了離散積分趨近律變結構控制策略，并應用于PMSM位置伺服系統，在電機內部參數攝動和外部參數擾動下，該控制策略提高了系統的魯棒性，實現了精確跟蹤并且提高了系統動態性能。然而文獻［7］和文獻［8］所設計的離散滑模控制器均存在不同程度的抖振，這對機電系統十分有害。

本文提出了一種新的離散滑模控制方法，并應用于PMSM調速系統之中，實現了良好的速度跟蹤能力和對電機參數攝動及外干擾的強魯棒性。通過引入冪次函數，消除了系統的抖振;通過引入一步延時干擾估計實現對干擾的補償。仿真和實驗驗證了所提方法的優越性。

1 PMSM數學模型

PMSM的定子和普通電勵磁三相同步電動機的定子相似。在建模及分析、設計過程中常作以下假設:轉子永磁磁場在氣隙空間分布為正弦波，定子電樞繞組中的感應電動勢也為正弦波;忽略定子鐵心飽和，認為磁路為線性，電感參數不變;不計鐵心渦流與磁滯損耗;轉子沒有阻尼繞組。

在以上假設下，建立d－q坐標系下的PMSM數學模型，其電壓方程:

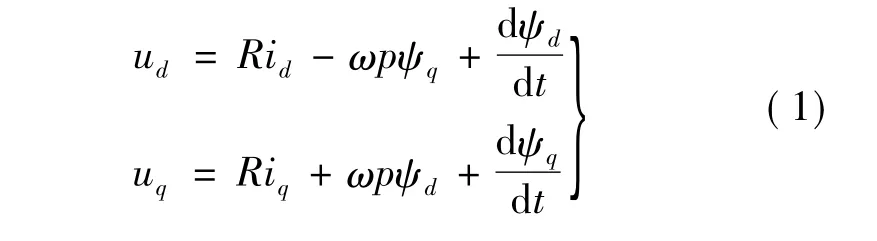
磁鏈方程:

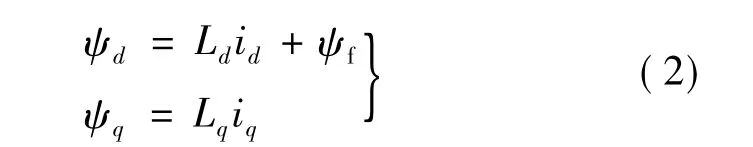
對于表面式PMSM，有Ld=Lq=L，所以轉矩方程:

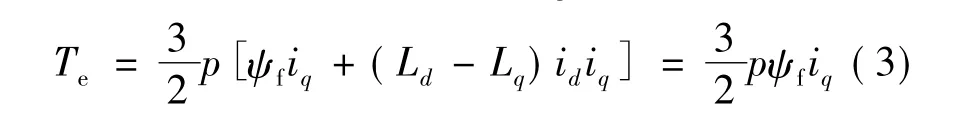
機械運動方程:

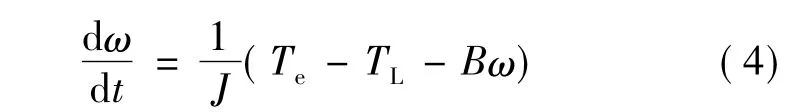
式中:ud、uq為 d、q 軸的電壓;id、iq為 d、q 軸的電流;Ld、Lq為d、q軸電感;R為定子電阻;p為電機極對數;ψf為永磁體與定子交鏈的磁鏈;Te為電磁轉矩;TL為負載轉矩;J為轉動慣量;B為粘滯系數;ω為轉子機械角速度。

采用id=0的PMSM轉子磁場定向控制，根據式(1)和式(2)可得:

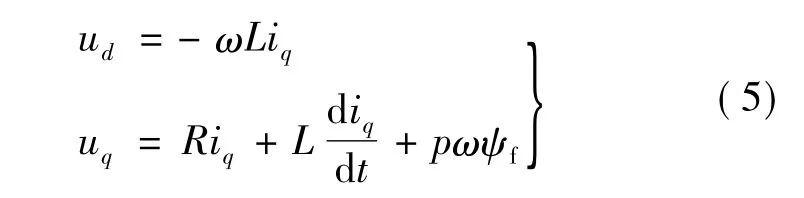
選取狀態變量x1為電機轉速x1=ω，狀態變量x2為q軸電流x2=iq，控制u為q軸定子電壓u=uq，由式(3)～ 式(5)得:

在電機工作過程中會產生熱量，定子繞組的電阻會隨溫度的升高而變大，所以當R變化時，PMSM的模型應為:

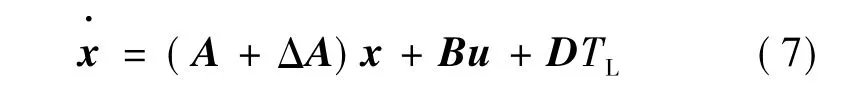
由于電機轉速、電機的交軸電流、定子電阻變化和負載干擾都是有界的，故令:

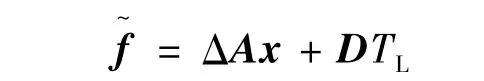
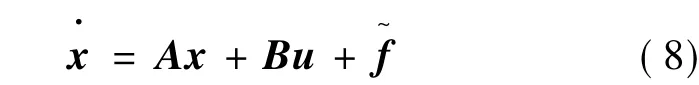
取采樣周期為T，采用零階保持器，將式(8)離散化可得:

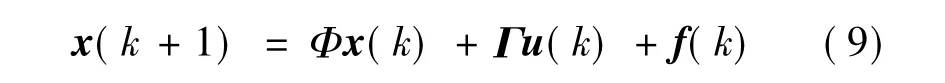
控制目標:在電機參數攝動和負載干擾作用下，針對式(9)設計離散滑模控制器，使電機轉速能較好地跟蹤參考轉速，并且系統不存在高頻抖振。

2 離散滑模控制器設計

2.1 冪次函數

冪次函數 fal(s，α，δ)是一種非線性函數［9］，利用它可以產生許多智能性的功能，其表達式:

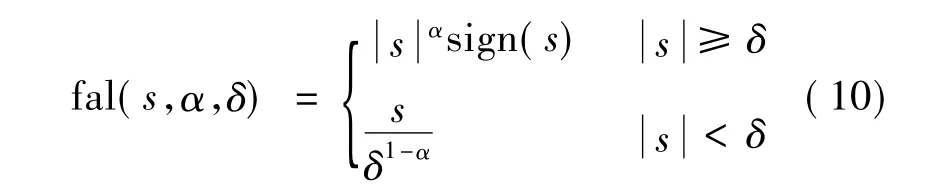
式中:0＜δ＜1。

2.2 滑模控制器的設計

2.2.1 滑模面函數的選擇

設電機的參考轉速信號為rref(k)，取離散線性切換函數:

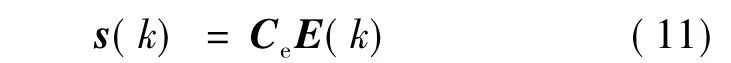
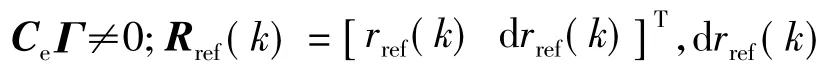
2.2.2 離散滑模控制器設計

引入冪次函數，考慮離散趨近律:

式中:f(k－1)=x(k)－Φx(k－1)－Γu(k－1)，稱為一步延時干擾估計［10］。

由式(14)的表達式可以看出，控制量中不含有未知項，是可執行的控制律。

3 系統魯棒性研究

定理:對于式(9)，在式(14)控制量的作用下，切換函數s(k)無抖振、單調的收斂于原點的某個區域，區域的界是與干擾估計誤差有關的某一數值，且系統不存在高頻抖振現象。以下進行定理證明。

令干擾估計誤差:

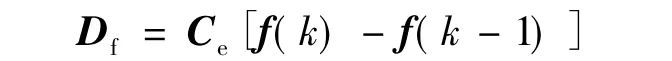
式(12)化簡:

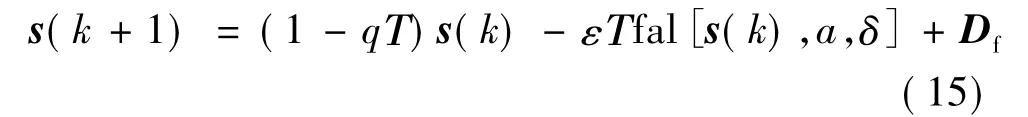
針對式(12)，分析滑模面s(k)的運動趨勢。

(1)0≤Df＜ qΤδ+εΤδa時

(a)s(k)≥δ時，式(15)化為:

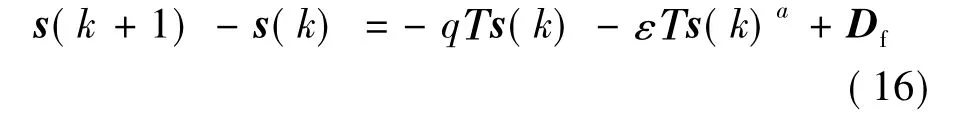
設 Δs(k)=s(k+1)－s(k)，得:

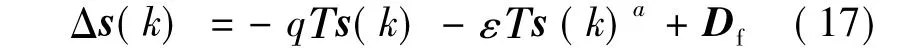
對式(17)兩邊求s(k)的導數:

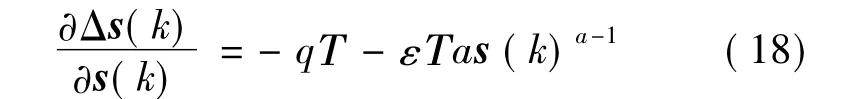
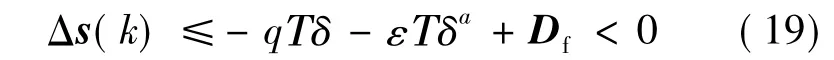
由Δs(k)≤0知，s(k)遞減。故當s(k)≥δ，s(k)遞減，直到進入0≤s(k)＜δ的范圍。

(b)0≤s(k)＜δ時，式(15)化為:

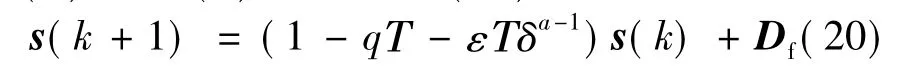
對于式(20)，有:

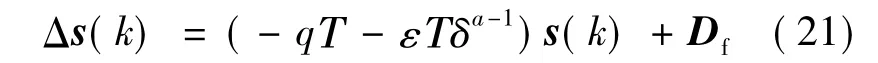
對于式(21)，有:

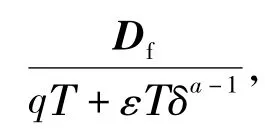
(c)s(k)≤－δ時，式(15)化為:

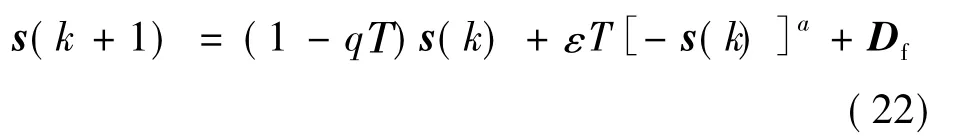
針對式(22)，有:

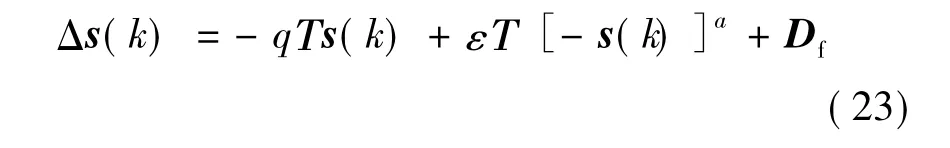
對式(23)兩邊求s(k)的導數為:

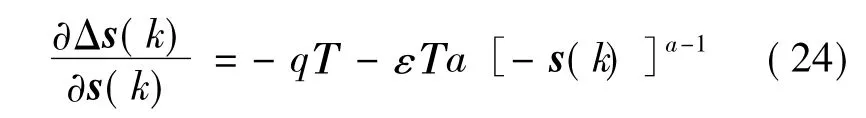
由Δs(k)＞0，可知s(k)遞增。故當s(k)≤－δ時，s(k)遞增，直到進入－δ＜s(k)＜0的范圍。

兩組患者治療前的各項指標無顯著差異(P<0.05),而在治療后組間差異存在統計學意義(P<0.05),詳情見表2。

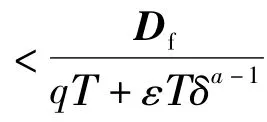
故當－δ＜s(k)＜0時，s(k)遞增，直到進入s(k)≥0的范圍，由上文推導可知，一旦s(k)進入s(k)≥0的范圍，函數s(k)將單調收斂于h1。

(2)Df≥qΤδ+εΤδa時

(a)s(k)＜0時，由式(21)和式(25)可知Δs(k)＞0，s(k)遞增。故當s(k)＜0時，s(k)遞增，直至進入s(k)＞0的范圍。

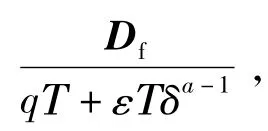
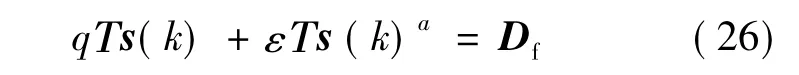
假設s(k)=h2使得式(26)成立，由減函數的性質可知:

s(k)＜h2時，Δs(k)＞0，s(k)遞增;

s(k)=h2時，Δs(k)=0，s(k)不變。

故s(k)≥δ時，函數s(k)單調收斂到h2，且不會出現穿越s(k)=h2現象。

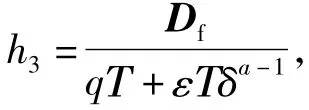
(4)當Df≤ －qΤδ－ εΤδa，同理可得，函數 s(k)單調收斂到s(k)=h4(s(k)=h4使得 －qΤs(k)+εΤ［－s(k)］a=－Df成立)，且不會出現穿越h4的現象。

上述分析結論可知，切換函數s(k)無正負交替、單調收斂于與干擾估計誤差相關的某個數值，且不會出現穿越現象，這就從根本上避免了系統高頻抖振現象的發生。定理得證。

通過定理的證明可知，式(14)的控制律在系統受到未知有界干擾時可以保證滑模面函數s(k)單調收斂到原點的某個鄰域，即系統狀態在滑模面的某一鄰域內作準滑模運動，且準滑模帶寬與干擾估計誤差有關。

4 仿真分析

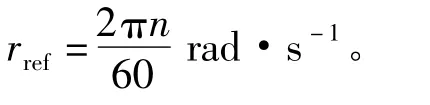
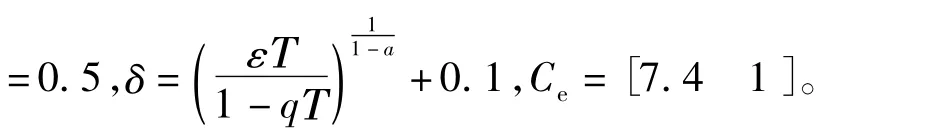
PI控制器參數 Kp=0.08，Ki=0.2。

本文算法與PI控制進行仿真對比研究，仿真結果如圖1～圖4所示。

(1)突加負載情況

在t≥2 s時加入TL=1 N負載，本文方法和PI控制進行仿真比較研究，仿真結果如圖1和圖2所示。

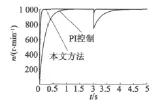
圖1 PMSM調速系統的轉速對比

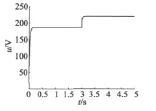
圖2 PMSM的電壓輸入

(2)參數攝動情況

負載為零時，在時間t≥2 s時，電機的電阻發生攝動變為2R，本文方法和PI控制進行仿真比較研究，仿真結果如圖3和圖4所示。

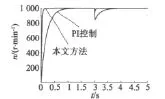
圖3 PMSM調速系統的轉速對比

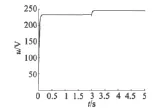
圖4 PMSM的電壓輸入

由圖1和圖3可以看出，與傳統PI控制方法相比，本文方法設計的PMSM調速系統具有較快的響應速度，并且對外界干擾和參數攝動具有較強的魯棒性。由圖2和圖4可以看出，本文所設計的控制系統的電壓輸入不存在高頻抖振。

5 實驗研究

本文采用TMS320LF2407A芯片作為核心構建實驗平臺，對一臺實際電機進行實驗研究。給定轉速 n=1 000 r/min，在 t=3.6 s時突加負載，實驗結果如圖5所示。

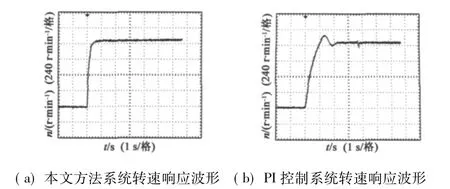
圖5 系統轉速響應波形

在電機實際運行中，電機繞組電阻隨著溫度升高會發生一定的變化，電機受到負載干擾時，電機自身的慣性能夠克服一部分負載干擾的影響，加上電力電子器件開關滯后等因素的影響，實際電機轉速響應與仿真中會有不同。由圖5可知，PI控制器控制下的系統，轉速響應較慢，有一定的超調，并且對突加負載的魯棒性較差，本文方法設計的調速系統，轉速響應較快，略有超調，對突加負載有較好的魯棒性。

6 結 語

本文提出了一種新的離散滑模控制方法，并應用到PMSM的調速系統中，實現了良好的速度跟蹤能力和對電機參數攝動以及外部干擾的強魯棒性;控制電壓輸入不存在高頻抖振，消除了傳統離散滑模控制中的抖振對機電系統的危害。仿真和實驗均驗證了該控制器的控制效果。

［1］ 孫強，程明，周鶚，等.新型雙凸極永磁同步電機調速系統的變參數 PI控制［J］.中國電機工程學報，2003，23(6):117 －123.

［2］ 劉金琨.滑模變結構控制MATLAB仿真［M］.北京:清華大學出版社，2005.

［3］ Lai C K，Shyu K K.A novel motor drive design for incremental motion system via sliding mode control method［J］.IEEE Trans.on Industrial Electronics，2005，2(52):499 －507.

［4］ 李鴻儒，顧樹生.基于神經網絡的PMSM自適應滑模控制［J］.控制理論與應用，2005，3(22):461 －464.

［5］ 賈洪平，賀益康.永磁同步電機滑模變結構直接轉矩控制［J］.電工技術學報，2006，21(1):1 －6.

［6］ 汪海波，周波，方斯琛.永磁同步電機調速系統的滑模控制［J］.電工技術學報，2009，9(24):71－77.

［7］ 葛寶明，鄭瓊林，蔣靜坪，等.基于離散時間趨近律控制與內模控制的永磁同步電動機傳動系統［J］.中國電機工程學報，2004，11(24):106 －111.

［8］ 瞿少成，孟光偉，姚瓊薈.PMSM位置伺服系統的離散積分變結構控制［J］.電機與控制學報，2003，2(7):136 －139.

［9］ 韓京清.自抗擾控制技術［M］.北京:國防工業出版社，2008.

［10］ Young K D，Utkin V I，Ozguner U.A control engineer＇s guide to sliding mode control［J］.IEEE Trans.on Control Systems Technology，1999，7(3):328 －342.