基于RBF控制的開關(guān)磁阻電動(dòng)機(jī)直接轉(zhuǎn)矩控制

劉春元，王勉華，王宗剛

(1.河西學(xué)院，甘肅張掖734000;2.西安科技大學(xué)，陜西西安710054)

0 引 言

開關(guān)磁阻電動(dòng)機(jī)(以下簡稱SRM)是繼異步電動(dòng)機(jī)之后的又一種新型電機(jī)，具有結(jié)構(gòu)簡單、起動(dòng)轉(zhuǎn)矩大、控制參數(shù)靈活、調(diào)速性能優(yōu)越等優(yōu)點(diǎn);但是SRM是雙凸極結(jié)構(gòu)，通常工作在磁飽和狀態(tài)，導(dǎo)致了SRM的電磁特性呈高度非線性，難以用一個(gè)精確的數(shù)學(xué)表達(dá)式來描述SRM的電磁關(guān)系［1－2］。目前，對SRM主要的研究方向集中為兩點(diǎn)，即電機(jī)本體的設(shè)計(jì)以及控制方法的研究。本文主要從控制方面展開論述。

常規(guī)PID控制器由于結(jié)構(gòu)簡單、實(shí)現(xiàn)容易、控制方便等優(yōu)點(diǎn)，仍處于主導(dǎo)地位，得到了廣泛應(yīng)用，其核心就是參數(shù)的整定。但隨著控制對象系統(tǒng)的越來越復(fù)雜，常規(guī)PID控制器的參數(shù)是固定不變的，在非線性系統(tǒng)中很難達(dá)到良好的控制效果。由于SRM的電磁關(guān)系呈現(xiàn)為嚴(yán)重的非線性，所以常規(guī)的控制方法很難達(dá)到控制的預(yù)期效果。近年來，隨著人工神經(jīng)網(wǎng)絡(luò)和控制理論(特別是智能控制理論)的逐漸發(fā)展，由人工神經(jīng)網(wǎng)絡(luò)構(gòu)成的自適應(yīng)控制器逐漸在非線性系統(tǒng)中得到了廣泛的應(yīng)用，解決了非線性和不確定系統(tǒng)的控制方面難題。國內(nèi)外專家學(xué)者將神經(jīng)網(wǎng)絡(luò)控制器應(yīng)用于開關(guān)磁阻電動(dòng)機(jī)調(diào)速系統(tǒng)(以下簡稱SRD)中，取得了很好效果。文獻(xiàn)［3］提出了單神經(jīng)元PID控制器;文獻(xiàn)［4］是以BP神經(jīng)網(wǎng)絡(luò)整定的PID控制器;文獻(xiàn)［5］提出了模糊PID控制器等智能控制器，以實(shí)現(xiàn)對復(fù)雜系統(tǒng)的控制?；诖?，本文提出了一種基于RBF神經(jīng)網(wǎng)絡(luò)自整定的PID控制器，利用直接轉(zhuǎn)矩控制的思想，針對SRM嚴(yán)重的非線性，利用神經(jīng)網(wǎng)絡(luò)構(gòu)成SRM的控制器。為了進(jìn)行對比，本文同時(shí)也研究了常規(guī)PI的控制方法，結(jié)果表明，本文的方法與單一常規(guī)PI控制器相比，具有控制精度高、響應(yīng)時(shí)間短、超調(diào)較小的優(yōu)點(diǎn)，并且當(dāng)系統(tǒng)中存在干擾時(shí)，具有很好的自適應(yīng)性能力以及很好的魯棒性。

1 SRM數(shù)學(xué)模型

(1)電壓方程

根據(jù)電磁感應(yīng)定理和能量損耗定理，施加在定子各相繞組兩端的電壓，等于定子因磁鏈變化而產(chǎn)生的感應(yīng)電勢和電阻壓降之和，即:

式中:U、R、i依次是電機(jī)定子相電壓、相電阻和相電流;θ為電機(jī)轉(zhuǎn)子與定子的相對位置角;ψ(i，θ)為電機(jī)定子的相繞組磁鏈。

(2)磁鏈方程

對于SRM，兩相之間的自感相對互感要大得多，通常可以將互感忽略不計(jì)。這樣一來就可以用下式來描述SRM每相繞組磁鏈ψ(i，θ):

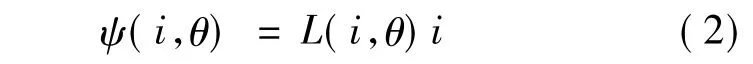
式中，相電感的值是由相電流i和轉(zhuǎn)子位置角θ確定，且它們之間為非線性函數(shù)，故很難用解析的方法就得式(1)的解析值，目前主要的方法是通過有限元、神經(jīng)網(wǎng)絡(luò)擬合等方法進(jìn)行計(jì)算。

(3)轉(zhuǎn)矩方程

在一個(gè)控制周期中，電機(jī)的電流基本上不發(fā)生變化。由SRM的瞬時(shí)轉(zhuǎn)矩理論可知，轉(zhuǎn)矩可以用機(jī)械能跟轉(zhuǎn)子位置角的導(dǎo)數(shù)求取，即可以用下式表達(dá):

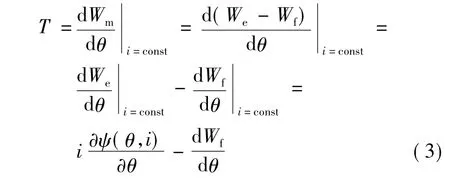
式中:Wm為機(jī)械能;We為磁共能;Wf為磁場儲(chǔ)能。

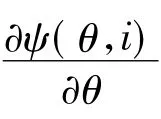
(4)運(yùn)動(dòng)方程

按照力學(xué)定律可列出SRM的轉(zhuǎn)子機(jī)械運(yùn)動(dòng)方程:

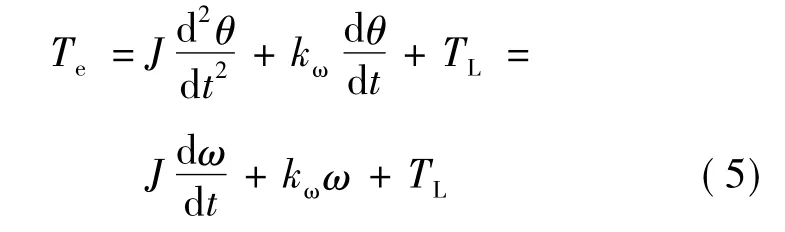
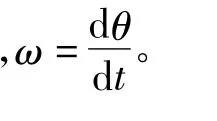
2 開關(guān)磁阻電動(dòng)機(jī)調(diào)速系統(tǒng)(SRD)

SRD由控制器、功率變換器、位置檢測、電流檢測和SRM電機(jī)本體構(gòu)成［6］，其結(jié)構(gòu)圖如圖1所示。

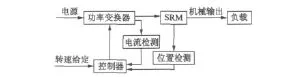
圖1 SRD結(jié)構(gòu)框圖

在本文中，利用直接轉(zhuǎn)矩控制構(gòu)成SRD系統(tǒng)，其結(jié)構(gòu)圖如圖2所示。內(nèi)環(huán)包括磁鏈估算和轉(zhuǎn)矩估算。磁鏈估算通過式(1)的變形即 φ=∫(U－iRs)dt得到，然后跟給定磁鏈比較，得到磁鏈差;轉(zhuǎn)矩估算由SRM的輸出模塊給定;外環(huán)由具有自適應(yīng)功能的RBF神經(jīng)網(wǎng)絡(luò)控制器，輸入為給定速度與實(shí)際速度輸出之差，經(jīng)過RBF神經(jīng)網(wǎng)絡(luò)控制器，得到輸出轉(zhuǎn)矩T*，其值跟SRM模塊的輸出轉(zhuǎn)矩T比較，得到轉(zhuǎn)矩差值ΔT。送入開關(guān)表的信號(hào)為轉(zhuǎn)矩差ΔT、磁鏈差Δψ以及區(qū)間判斷信號(hào)Zone，利用直接轉(zhuǎn)矩控制原理，控制功率變換器中的開關(guān)信號(hào)，以達(dá)到對磁鏈的控制，進(jìn)而實(shí)現(xiàn)對轉(zhuǎn)矩的精確控制。本文中，功率變換器選用不對稱半橋型結(jié)構(gòu)形式。

圖2 SRM直接轉(zhuǎn)矩控制結(jié)構(gòu)圖

3 RBF神經(jīng)網(wǎng)絡(luò)

近年來，RBF神經(jīng)網(wǎng)絡(luò)在非線性系統(tǒng)的建模、預(yù)測、分析等方面得到了廣泛的研究和應(yīng)用［7］。它是一種典型的由輸入層、隱含層、輸出層組成的三層前饋式神經(jīng)網(wǎng)絡(luò)，結(jié)構(gòu)圖如圖3所示。

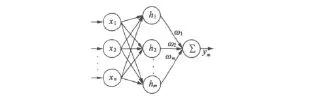
圖3 RBF神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)圖

輸入層為 X=［x1，x2，…，xn］，本文中，輸入為轉(zhuǎn)矩以及給定轉(zhuǎn)速與實(shí)際轉(zhuǎn)速的差值，隱含層為H=［h1，h2，…，hj，…，hm］T，節(jié)點(diǎn)選取為高斯函數(shù)，由線性神經(jīng)元組成。輸出為所有隱含層節(jié)點(diǎn)的輸出之和。

對于單個(gè)網(wǎng)絡(luò)輸出的RBF網(wǎng)絡(luò)，第k個(gè)隱含層單元的輸出:

式中:‖ ‖表示歐式范數(shù);Xi為第i個(gè)輸入向量;cj為第j個(gè)隱含層節(jié)點(diǎn)的中心;bj為第j個(gè)隱含層節(jié)點(diǎn)的寬度。

整個(gè)網(wǎng)絡(luò)的輸出方程:

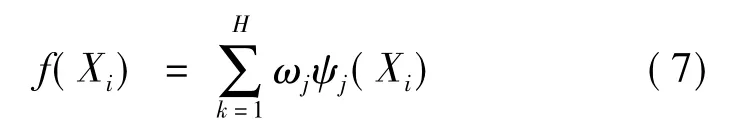
式中:ωj為第j個(gè)隱含層節(jié)點(diǎn)與輸出層節(jié)點(diǎn)的連接權(quán)值;H為總的隱含層節(jié)點(diǎn)數(shù)。

定義辨識(shí)網(wǎng)絡(luò)的性能指標(biāo)Jm:

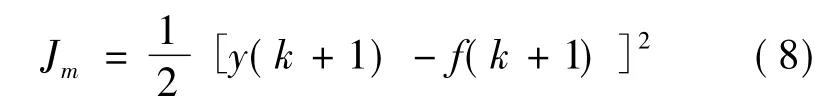
式中:f(k+1)為系統(tǒng)的實(shí)際輸出;y(k+1)為系統(tǒng)的期望輸出。本文中，cj、bj、ωj參數(shù)的確定，按照梯度下降法進(jìn)行計(jì)算，即有下式確定:

式中:α為動(dòng)量因子;η為學(xué)習(xí)速率。

4 RBF速度調(diào)節(jié)器設(shè)計(jì)

針對SRM電磁嚴(yán)重的非線性，采用結(jié)構(gòu)簡單的常規(guī)PID調(diào)節(jié)器很難實(shí)現(xiàn)對其的精確控制。利用具有自適應(yīng)的神經(jīng)網(wǎng)絡(luò)控制器，可以根據(jù)參數(shù)的變化，調(diào)節(jié)器發(fā)生相應(yīng)的變化，根據(jù)神經(jīng)網(wǎng)絡(luò)能任意逼近任何非線性函數(shù)的特點(diǎn)，本文提出了基于RBF神經(jīng)網(wǎng)絡(luò)整定的PID控制。仿真實(shí)現(xiàn)圖如圖4所示。其中輸入為給定速度n*與輸出轉(zhuǎn)速n之差Δn以及輸出轉(zhuǎn)矩Te，輸出為參考轉(zhuǎn)矩T*和PID參數(shù)。T*通過與Te比較，輸入滯環(huán)調(diào)節(jié)器對轉(zhuǎn)矩進(jìn)行調(diào)節(jié)。

圖4 RBF控制器的仿真實(shí)現(xiàn)

nnrbf_pid由S－function實(shí)現(xiàn)，主要功能是通過梯度下降法對 cj、bj、ωj參數(shù)的調(diào)整，完成基于 RBF網(wǎng)的PID調(diào)節(jié)器。為了使控制器更接近實(shí)用，在輸出環(huán)節(jié)之后增加一個(gè)限幅環(huán)節(jié)。

5 仿真結(jié)果及分析

本文在MATLAB中建立了SRM的直接轉(zhuǎn)矩控制，控制器采用上述的RBF自適應(yīng)控制。調(diào)速系統(tǒng)的仿真模型，如圖5所示。

圖5 整體仿真圖

本文中，以60 kW、四相8/6結(jié)構(gòu)的SRM為研究對象，給定轉(zhuǎn)速n=1 000 r/min。開始時(shí)，系統(tǒng)運(yùn)行在空載狀態(tài)，即TL=0，同時(shí)為了驗(yàn)證該系統(tǒng)的抗干擾能力，當(dāng)系統(tǒng)運(yùn)行0.4 s后，使系統(tǒng)由空載轉(zhuǎn)換為帶TL=12 N·m的負(fù)載，于0.75 s時(shí)再變?yōu)榭蛰d，在此過程中，要求電機(jī)的速度n要穩(wěn)定在給定轉(zhuǎn)速1 000 r/min。為了與PI控制器進(jìn)行比較，仿真時(shí)控制器分別采用了PI控制與RBF兩種控制方法，局部速度響應(yīng)曲線如圖6所示。

圖6 局部速度響應(yīng)曲線

從圖6中可以看出，僅僅利用PI控制器，系統(tǒng)的超調(diào)比較大，約為4%，且上升時(shí)間比較長;當(dāng)系統(tǒng)中存在干擾時(shí)，到達(dá)到所要求的速度，調(diào)節(jié)時(shí)間比較長;而用RBF神經(jīng)網(wǎng)絡(luò)控制器，系統(tǒng)的超調(diào)明顯減小，當(dāng)存在干擾時(shí)，系統(tǒng)的自適應(yīng)能力比較強(qiáng)，速度能一直維持在給定速度，抗干擾能力好。控制效果明顯優(yōu)于單一的PI控制器。

圖7給出了系統(tǒng)的輸出轉(zhuǎn)矩曲線?？梢钥闯?，系統(tǒng)的起動(dòng)轉(zhuǎn)矩比較大，在限定值附近。系統(tǒng)穩(wěn)定運(yùn)行時(shí)，轉(zhuǎn)矩脈動(dòng)僅為±1 N·m，當(dāng)加入干擾時(shí)，轉(zhuǎn)矩能夠很快地穩(wěn)定在給定的值附近，充分證明了利用此種方法能有效地減少系統(tǒng)的轉(zhuǎn)矩脈動(dòng)。

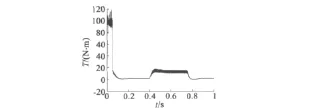
圖7 轉(zhuǎn)矩曲線

為了驗(yàn)證本文所闡述的直接轉(zhuǎn)矩控制對SRM的控制效果，圖8同時(shí)給出了直接轉(zhuǎn)矩控制與電流斬波控制的磁鏈軌跡圖。從圖中可以看出，前者幅值被限定在滯環(huán)寬度內(nèi)，磁鏈軌跡是一個(gè)圓形，磁鏈幅值基本恒定，達(dá)到了直接轉(zhuǎn)矩控制的目的;后者磁鏈軌跡接近四邊形，達(dá)不到磁鏈幅值恒定的原則。從而證明了此種方法的控制效果要遠(yuǎn)遠(yuǎn)好于電流斬波控制的方法。

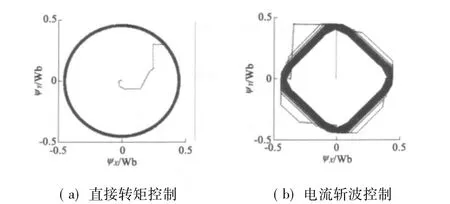
圖8 磁鏈軌跡

6 結(jié) 語

本文充分利用RBF神經(jīng)網(wǎng)絡(luò)泛化能力強(qiáng)和計(jì)算速度快的優(yōu)點(diǎn)，將直接控制控制技術(shù)與智能控制很好的結(jié)合起來，構(gòu)成SRD控制器。仿真結(jié)果表明，該種控制方法具有較好的穩(wěn)定性和動(dòng)態(tài)響應(yīng)能力;具有響應(yīng)時(shí)間短、超調(diào)小的優(yōu)點(diǎn);系統(tǒng)動(dòng)、靜態(tài)性能良好，并且保證了系統(tǒng)的抗干擾能力，對系統(tǒng)具有較高的控制精度，對具體的工程實(shí)踐有很好的指導(dǎo)意義。

［1］ 王宏華.開關(guān)磁阻電動(dòng)機(jī)調(diào)速控制技術(shù)［M］.北京:機(jī)械工業(yè)出版社，1995.

［2］ 吳建華.開關(guān)磁阻電機(jī)設(shè)計(jì)與應(yīng)用［M］.北京:機(jī)械工業(yè)出版社，2000.

［3］ 于力，歐陽紅林.一種基于單神經(jīng)元PID控制的多相永磁同步電動(dòng)機(jī)矢量控制系統(tǒng)［J］.微電機(jī)，2007，40(8):89 －92.

［4］ 廖芳芳，肖建.基于BP神經(jīng)網(wǎng)絡(luò)PID參數(shù)自整定的研究［J］.系統(tǒng)仿真學(xué)報(bào)，2005，17(7):1711 －1713.

［5］ 李麗娜，柳洪義.模糊PID復(fù)合控制算法改進(jìn)及應(yīng)用［J］.東北大學(xué)學(xué)報(bào)(自然科學(xué)版)，2009，30(2):274 －278.

［6］ 王勉華，梁媛媛.開關(guān)磁阻電機(jī)直接轉(zhuǎn)矩模糊PI控制器的設(shè)計(jì)［J］.電氣傳動(dòng)，2010，40(1):51 ～54.

［7］ 黃友銳，曲立國.PID控制器參數(shù)整定與實(shí)現(xiàn)［M］.北京:科學(xué)出版社，2010.