基于球Bessel函數的鋼球溫度分布均勻化時間計算

王小增，曾輝，楊久紅

(嘉應學院 電子信息工程學院，廣東 梅州 514018)

工業用球是重要的基礎零部件，而且在一些特殊條件下，常常需要特殊材質的球，來完成不同環境下所要求達到的功能。一些特殊材質球已廣泛應用于各個領域，如9Cr18,3Cr13不銹鋼，銅、鋁、鈦合金鋼以及瑪瑙、玻璃、陶瓷球等材質球的推廣應用。其中，軸承鋼球為廣泛使用的工業用球。為使鋼球具有所需要的力學性能、物理性能和化學性能，除合理選用材料和各種成形工藝外，熱處理工藝往往是必不可少的。在熱處理過程中，鋼球的溫度控制是一項重要的內容，直接影響著鋼球的熱處理質量，如果溫度控制不當，可能會導致鋼球開裂[1-3]。球Bessel函數常用于解決球對稱物體熱傳導定解問題[4-6]。下文采用能量守恒定律推導了鋼球的熱傳導方程，采用球Bessel函數給出了鋼球在溫度上升過程中熱傳導方程的解析解，并對不同半徑，初始溫度為900 ℃的鋼球溫度達到均勻分布的時間進行分析，通過擬合方法得出了計算公式。

1 球體熱傳導方程推導

作為球形傳熱體，如圖1所示，在笛卡爾坐標系中，球的溫度分布為u(x,y,z,t)，球形表面為∑，d∑為球體表面積微元，m為面積微元的外法線方向。

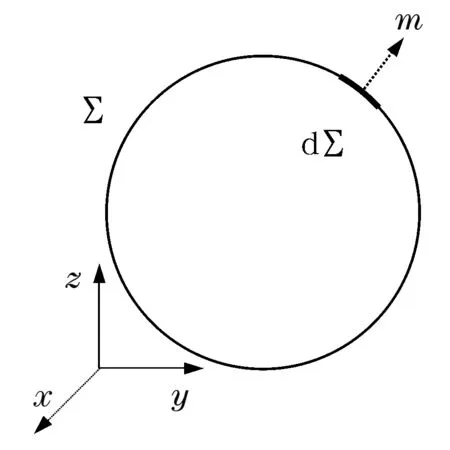
圖1 球模型

設Q1為單位時間內通過球形表面∑流出的熱量，Q2為球體單位時間內溫度升高所需的熱量，Q3為球體單位時間內熱源產生熱量，此系統無熱源，所以Q3為0。由能量守恒定律得

Q3=Q1+Q2，

(1)

即Q2=-Q1。

(2)

設qm為單位時間內由法線方向單位面積流出的熱量，由Fourier傳熱定律得

(3)

式中：λ為傳熱系數，W/(m2·℃)。

由(3)式得

(4)

由Gauss定理得

(5)

結合(2)式得

(6)

(7)

(8)

2 球Bessel函數理論

Helmholtz方程在球坐標下分離變量得到球Bessel函數[7-8]

(9)

式中：k，l為中間變量。

令y(x)=x-1/2v(x)，得到半奇數階球Bessel方程為

(10)

球Bessel方程的解可以用半奇數階球Bessel函數表示，其中

(11)

(12)

用φl表示上述函數可以得出遞推公式為

(13)

當l為整數時，

(14)

(15)

3 球體熱傳導方程求解

3.1 方程求解

設球體半徑為r0，初始溫度為u0，環境溫度為U0。球體內部溫度分布u(r,t)為定解問題，熱傳導方程為

(16)

其中，0≤r≤r0,t≥0。

為解決邊界條件非齊次問題，設u=v+U0，則關于v的方程為

(17)

選取球坐標系，邊界條件和初始條件與θ,φ無關，即v=v(r,t)滿足方程

(18)

設v(r,t)=R(r)T(t)，代入方程分離變量得

(19)

R(0)有界，R(r0)=0，則

T′+k2a2T=0 ，

(20)

式中：T為中間變量；T′為T的一階導數。

R(r)為0階球Bessel方程，解為0階球Bessel函數j0(kr),代入邊界條件有R(r0)=j0(kr0)=0，則

knr0=nπ;n=1,2…,N。

(21)

一般解為

(22)

代入初始條件有

(23)

展開以球Bessel函數為基函數的廣義Fourier級數可得

(-1)n+12(u0-U0),

(24)

最后得到方程的解為

(25)

3.2 級數收斂性分析

n取足夠大的定值可以保證溫度分布的計算精度，球體溫度分布的定解為

(26)

4 實例分析

4.1 鋼球溫度分布

某鋼球半徑 25 mm，鋼球初始溫度20 ℃，加熱爐溫度保持為900 ℃，密度為7 800 kg/m3,比熱容為448 J/(kg·℃),對流換熱系數為70 W/(m2·℃) ，n取10。得到鋼球溫度分布表達式為

(27)

鋼球在不同時間和不同位置的三維溫度分布如圖2所示。鋼球在不同位置隨時間的溫度分布如圖3所示，由圖可知，越靠近鋼球表面，溫度變化越劇烈，所以表面的微小裂紋容易導致鋼球的開裂。

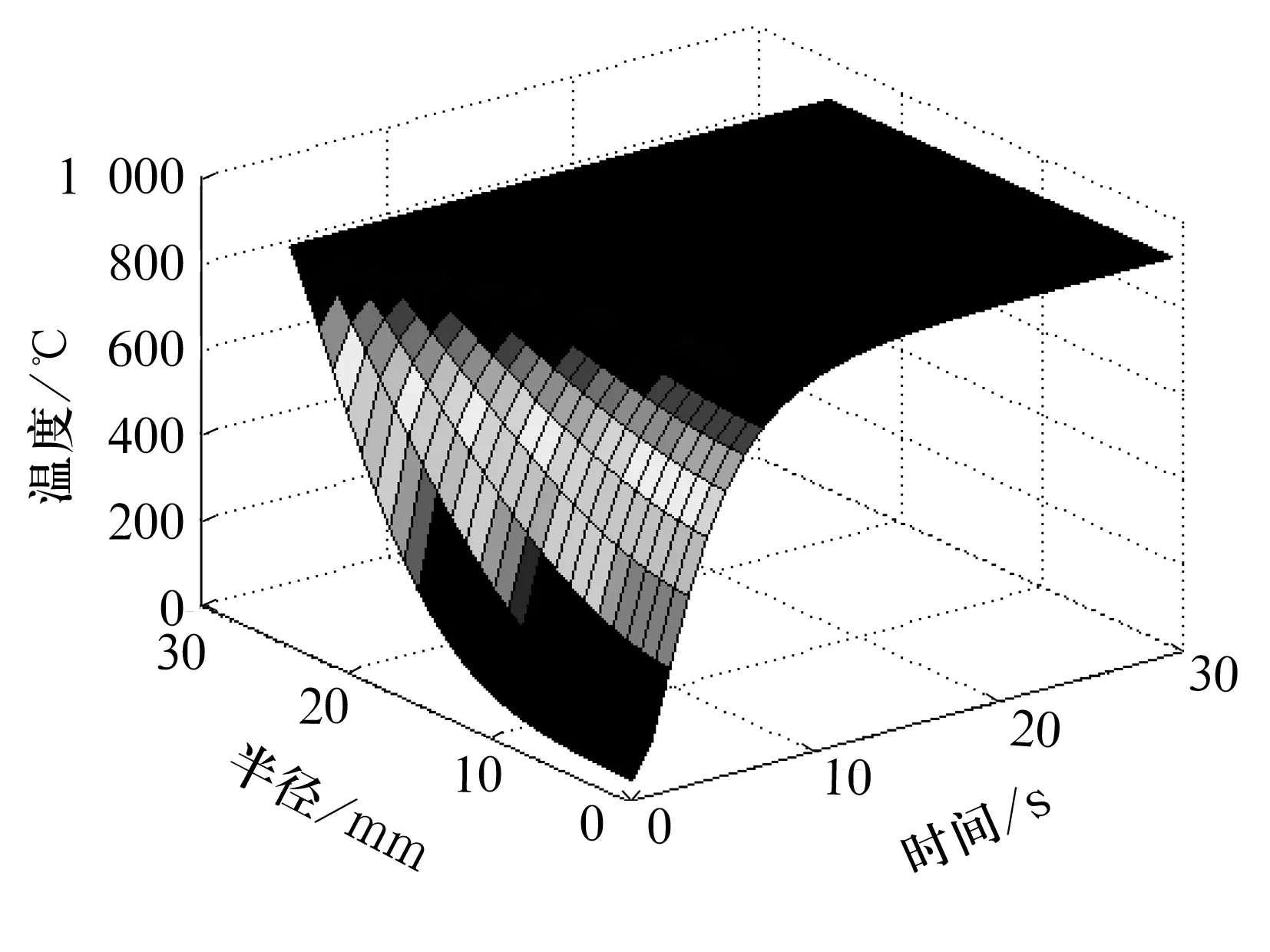
圖2 鋼球三維溫度分布

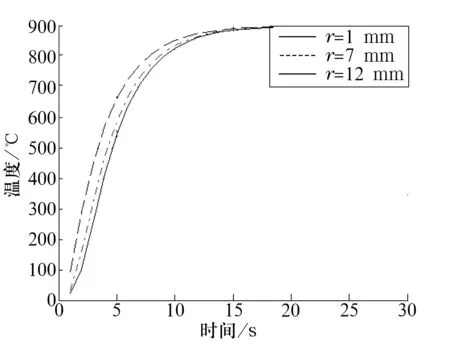
圖3 鋼球在不同位置隨時間的溫度分布

4.2 鋼球溫度分布均勻化時間計算

選取半徑為5 ～25 mm的鋼球代入(26)式進行計算，得出鋼球的各個位置溫度均達到899.99 ℃所需的時間如圖4所示，由圖4可知，分布均勻化所需時間為鋼球半徑的二次函數，所以進行二階擬合。

圖4 不同半徑鋼球溫度分布均勻化時間

設x為鋼球半徑，y為溫度分布均勻化所需時間，鋼球溫度分布均勻化時間計算的二階擬合公式為

y=0.04x2-1.469 2×10-15x+1。

(28)

鋼球半徑為12.7 mm時，由擬合公式計算的溫度分布均勻化所需時間為7.451 6 s；由溫度分布(26)式計算的結果為7.5 s，誤差為0.6%，可見由擬合公式計算不同半徑的鋼球溫度分布均勻化所需時間是可行的。

5 結論

(1)與鋼球內部相比，鋼球的表面溫度變化劇烈，所以鋼球表面的細微裂紋容易擴大造成整個鋼球在熱處理過程中開裂，在鋼球熱處理之前應確保鋼球無微小裂紋缺陷；

(2)由二次擬合公式可以精確計算不同半徑鋼球溫度分布均勻化所需的時間；

(3)由球Bessel函數得出鋼球熱傳導方程的解，可以方便地計算鋼球在不同位置以及不同時間的溫度值。