一個Hardy-Hilbert型不等式的推廣與加強
隆建軍
(攀枝花市大河中學,四川攀枝花617061)
設{an},{bn}為實數列,使得則有
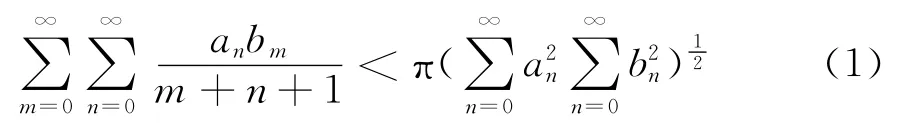
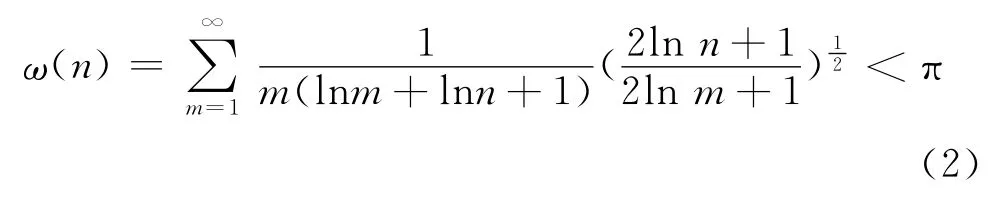
得到一個Hilbert型不等式

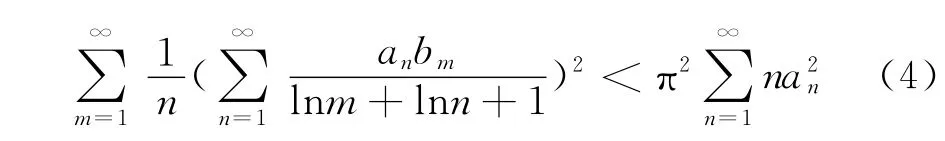
2007年,王衛宏,方波漪建立如下權系數不等式[6]:

得到一個Hilbert型不等式及其等價形式:
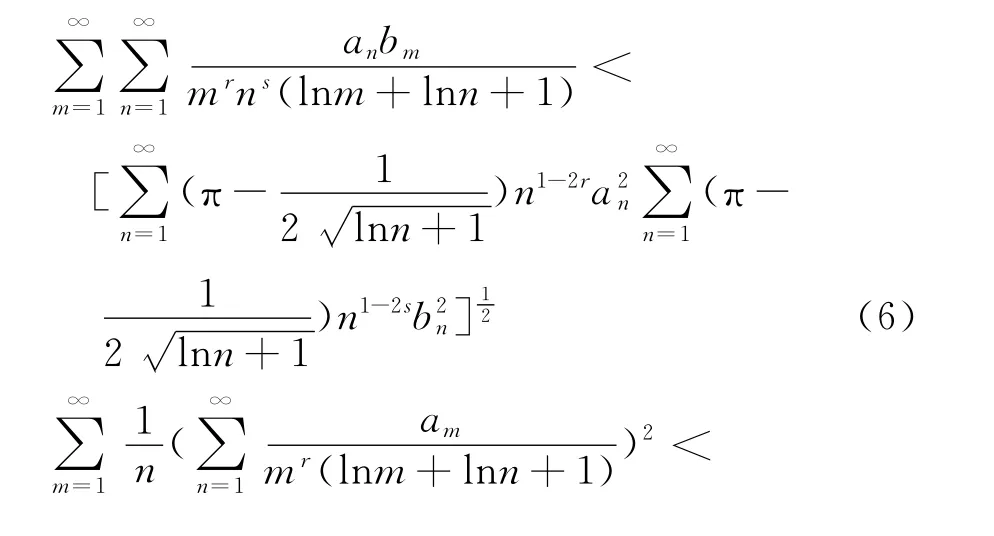
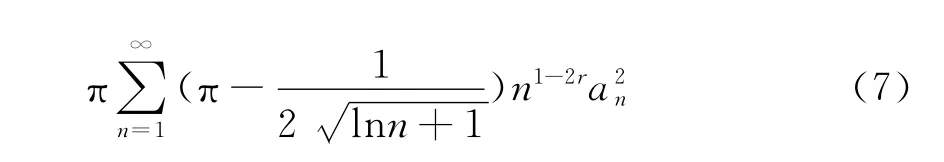
本文的目的是利用改進的Euler-Maclaurin公式,對權系數不等式(2)進行加強推廣,得到一個聯系二重級數形式
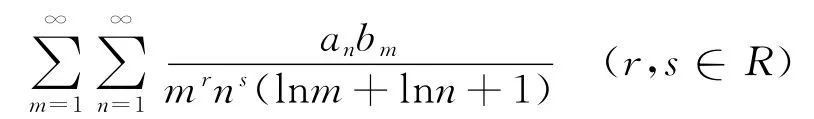
的Hardy-Hilbert型不等式,且本文結論是式(3)、式(4)的推廣和加強.
1 幾個引理
引理1[7]若f(2r)(x)>0(x)<0,x∈
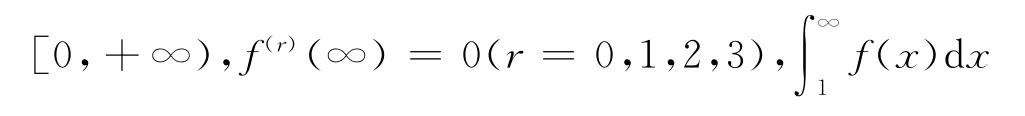
<∞,則有

引理2 下列權系數不等式成立:

證明 設
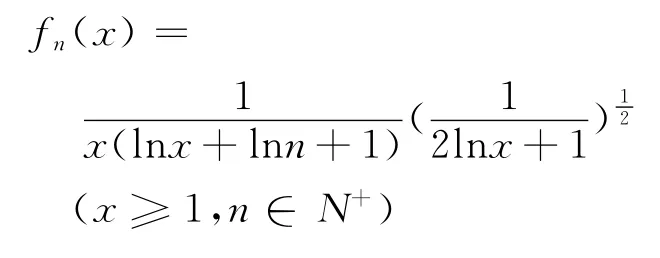
則
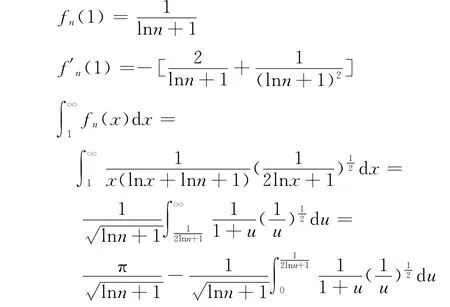
又由
W只與選取測試參量有關,當這些參量取通常值時:B=1 Hz,θ=0.9,ppd=1 mW,計算出陀螺靈敏度與腔體直徑D和品質因數Q值的關系(圖1)。所以,制備一種大直徑、高Q值的諧振腔,通過提高DQ乘積的形式,可以有效的提高陀螺的靈敏度。
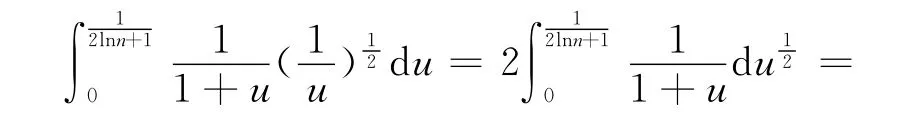
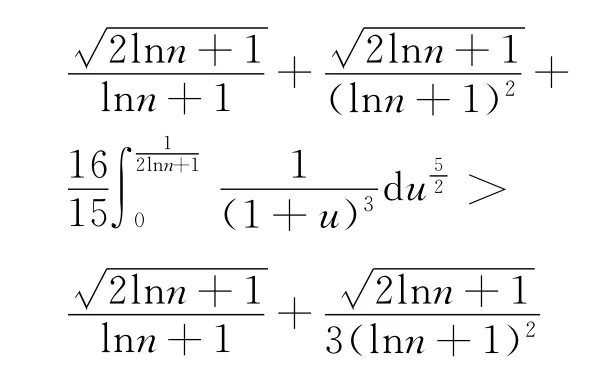
則
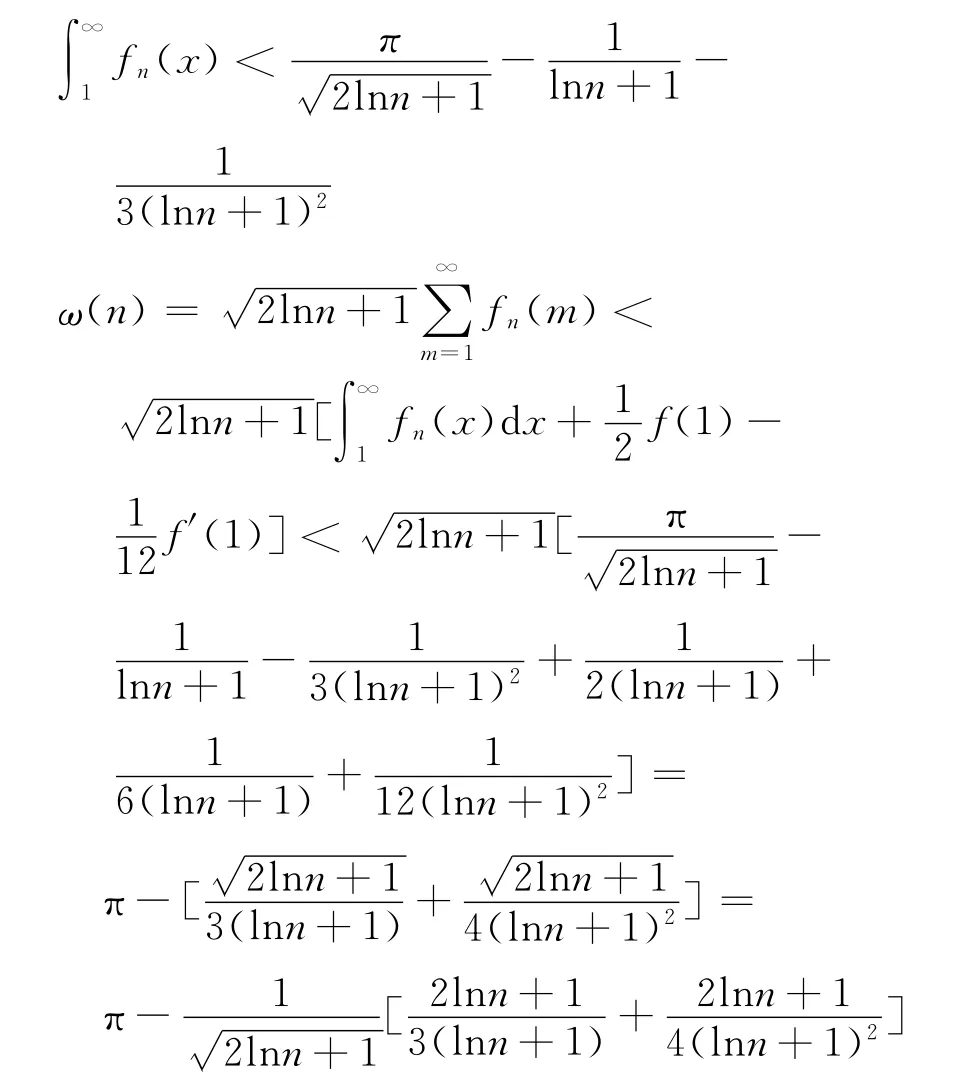
對n≥1,n∈N結合Bernoulli不等式,得

由以上計算可得
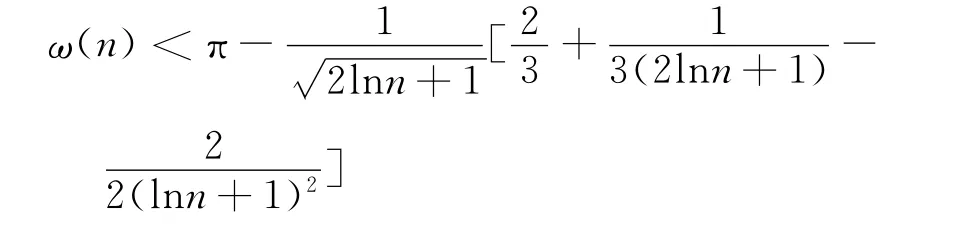
引理3 下列權系數不等式成立:
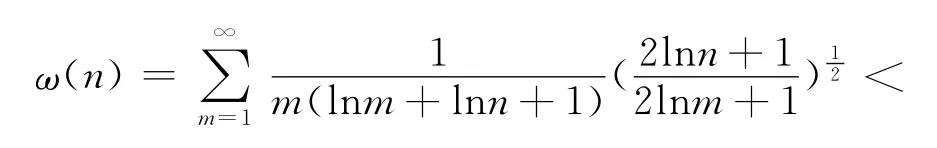
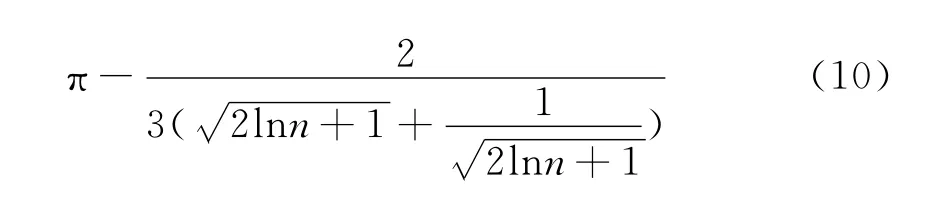
證明 由
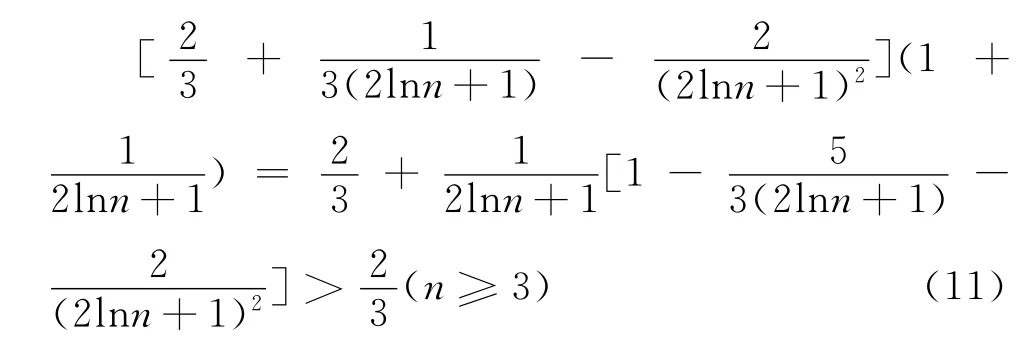
把式(11)代入式(9),即得
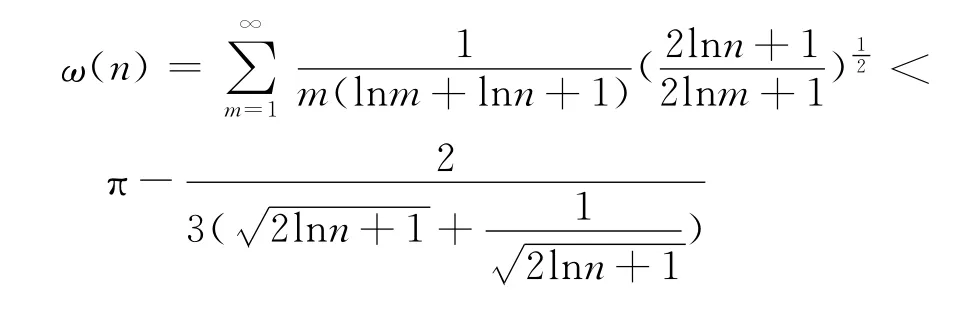

綜上可知引理3的式(10)成立.
2 主要結論及其應用
定理1 如果r,s∈R,{an},{bn}為實數列,使

證明 由帶權的Holder不等式,有
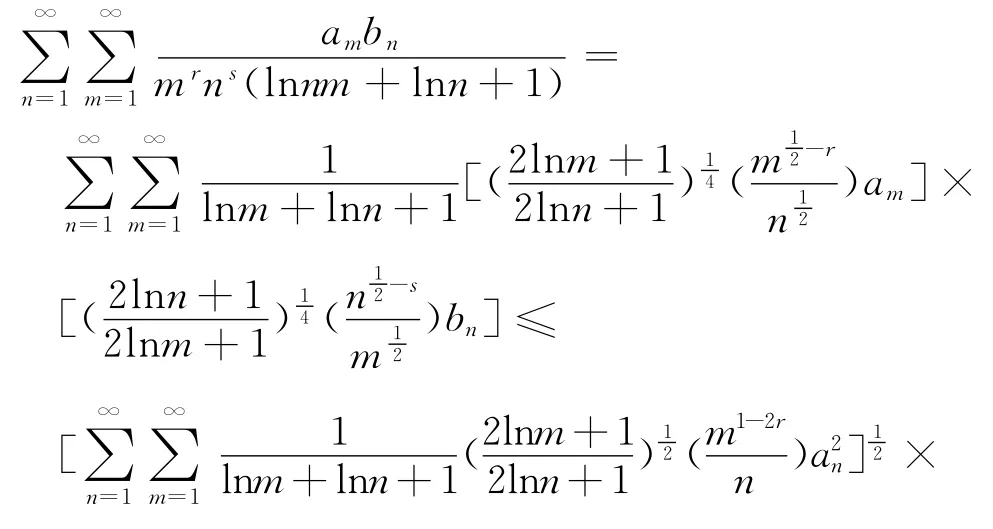

再由引理3,可得式(12).證畢.
定理2 如果r∈R,{an}為實數列,使得0<

證明 由ω(n)<π和帶權的Holder不等式,有

所以有
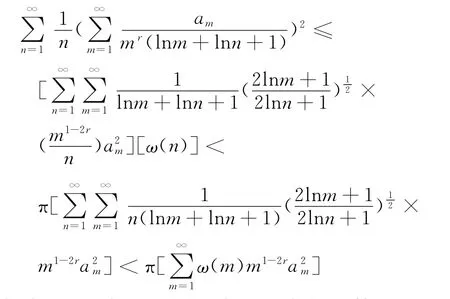
再由引理3的式(10),可知式(13)成立.證畢.
由于定理1中的式(12)和定理2中的式(13)帶有參數r,s,所以具有一般性.在式(12)和式(13)中對r,s適當取值,我們還可得到:
推論1 當r=s=0時,有
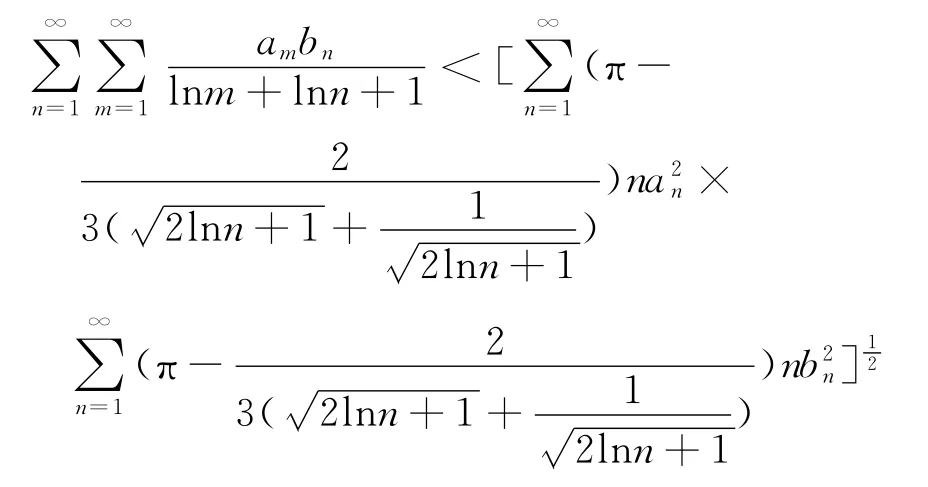

推論3 當r=0時,有
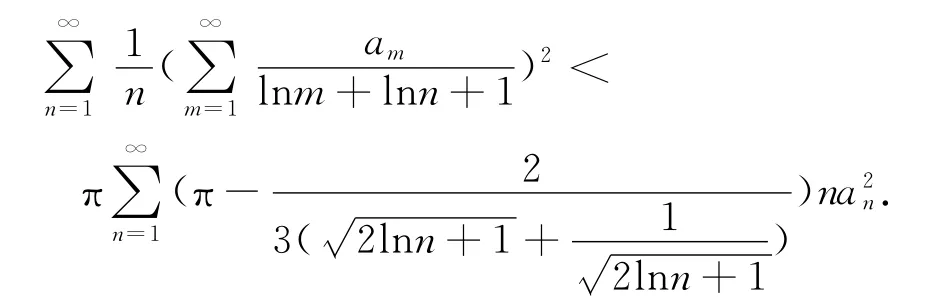
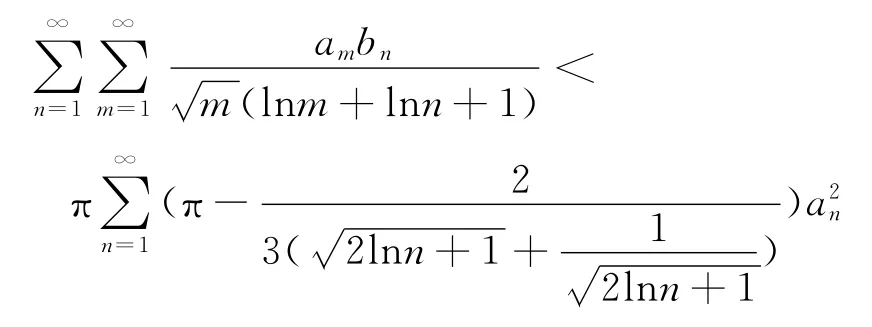
顯然,本文定理1和定理2都是全新的,同時推論1~推論4也是全新的結果.
[1] 匡繼昌.常用不等式[M] .濟南:山東科學技術出版社,2004.
[2] Yang B.On a strengthened version of the more accurate Hardy-Hilbert's inequality[J] .Acta Math.Sinica(N.S.),1999,42:1 103-1 110.
[3] Yang B C.A strengthened Hardy-Hilbert's inequality[J] .Proceedings of the Jangjeon Mathematical Society,2003(2),119-124.
[4] 席高文,柴新寬.一個推廣的Hardy-Hibert不等式及應用[J] .河南師范大學學報:自然科學版,2006,34(3):161-163.
[5] Yang B C.A new inequality similar to Hilbert's inequality[J] .J Math Anal Appl,1998,226:166-179.
[6] 王衛宏,方波漪.一個Hilbert型不等式的推廣與加強[J] .五邑大學學報:自然科學版,2007,20(4):19-23.
[7] 徐利治,王興華.數學分析的方法及例題選講[M] .北京:高等教育出版社,1985:81-98.

