單側-理想
趙士銀
(宿遷學院教師教育系,江蘇宿遷223800)
1 預備知識
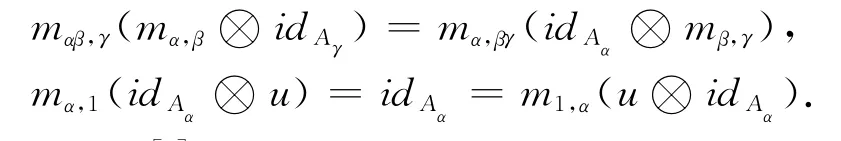
定義1[1]設H=({Hα,Δα,εα}α∈π,m,u)為π-代數,給定一簇K-線性映射S={Sα:Hα→,稱H為Hopfπ-代數,若H滿足以下三個條件:(1)對任意的α∈π,(Hα,Δα,εα)是余代數;(2)對任意的α,β∈:Hα?Hβ→Hαβ和u:K→P1都為余代數同態;(3)對任意的α∈π都有
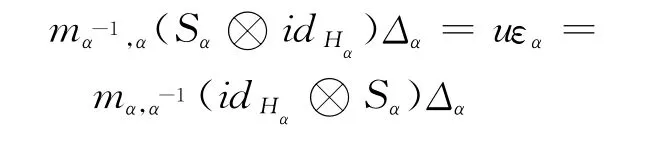
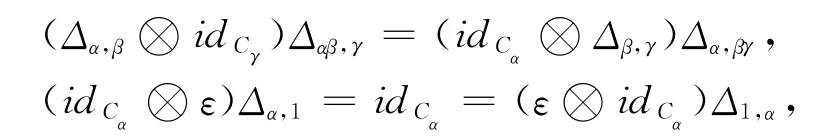
對任意的α,β,γ∈π.
定義2[1]設P=({Pα,mα,Δ,ε)為-余代數,給定一簇K-線性映射S={Sα:Pα→.稱P為Hopf-余代數,若P滿足以下三個條件:(1)對任意的α∈,(Pα,mα,uα)是代數;(2)對任意的α,β∈,Δα,β→Pα?Pβ和ε:P1→K都為代數同態;(3)對任意的α∈π都有
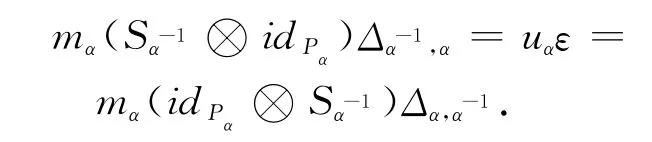
設f:V→W是線性映射,則有線性映射f*:W*→V*為〈f*(w*),v〉=〈w*,f(v)〉,其中w*∈W*,v∈V.設A=,m,u)為-代數,A0是A的對偶空間,由映射mα,β:Aα?Aβ→Aαβ,u:K→A1得到映射→(Aα?和u*→K*.定義ΔA0=→?}是如下合成(Aα?→?,定義:→K是如下合成:K*→K.
2 主要結論
本節我們首先給出局部有限維Hopfπ-代數H的對偶H0的代數結構.
證明 對于任意的α,β,γ∈π,任取x∈Aα,y∈Aβ,z∈Aγ,f∈一方面有:
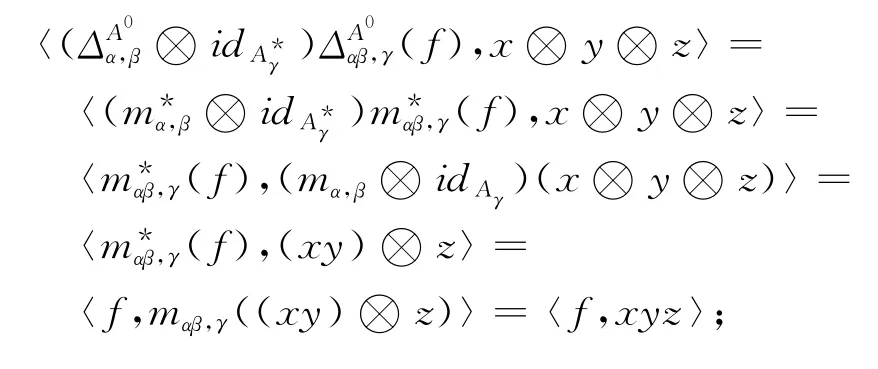
另一方面:
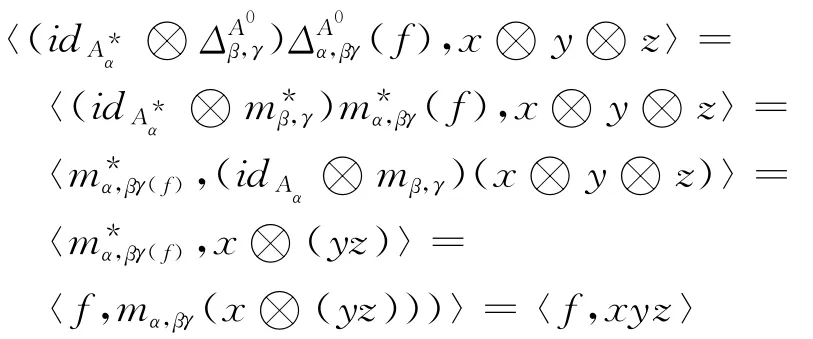
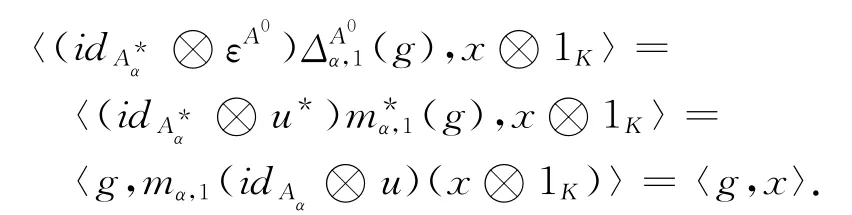
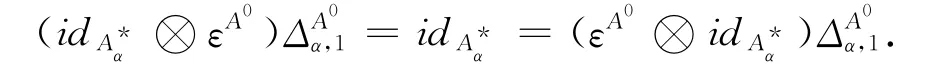
引理2 設H=({Hα,Δα,m,u)是局部有限維的Hopfπ-代數,則H的對偶空間H0=({,})可成為一個Hopf-余代數,其中
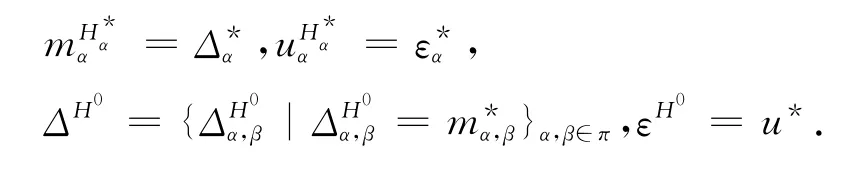
證明 首先,由于H=({Hα,m,u)是局部有限維Hopfπ-代數,由Hopfπ-代數的定義,H同時也是有限維的π-代數,從而由引理1可知,H的對偶空間H0=()是一個π-余代數.
其次,對于任意α∈π,由于(Hα,Δα,εα)是余代數,故由文獻[4] 得,()都是代數.
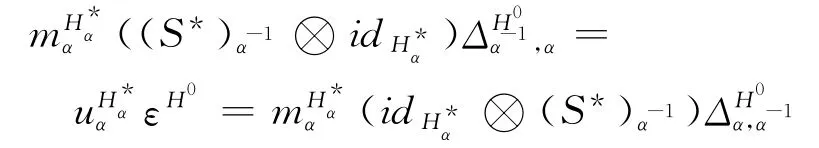
即可,其中S*=:=→Hα}α∈π.
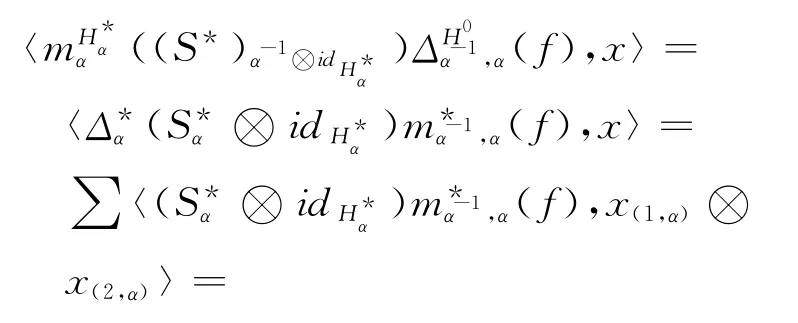
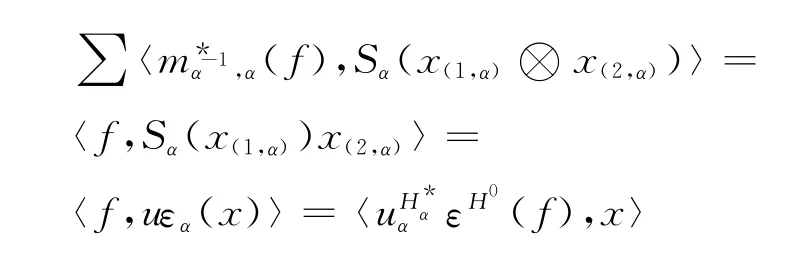
同理可證得
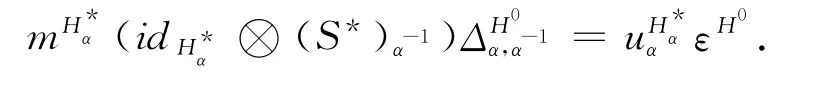
故對于任意的α∈π,
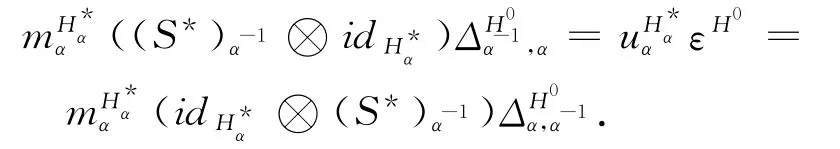
綜上所述,由Hopfπ-余代數的定義,H0=({,是一個Hopfπ-余代數.
同理有:若J={Jα|Jα?是H0的一個子空間簇,則定義J⊥=,其中={hα∈Hα|〈hα,jα〉=0,?jα∈Jα},則是J⊥=是H的一個子空間簇.
定義3[1]設A=,m,u)為一個-代數,W={Wα|Wα?是A=,m,u)的一簇子空間,若對于任意的α,β∈π都滿足:
(2)mα,β(Aα?Wβ)?Wαβ,則稱W={Wα|Wα為A=,m,u)的一個右-理想.
定義4[1]設C=,Δ,ε)為-余代數,I={Iα|Iα?是C=,Δ,ε)的一簇子空間,若對于任意的α,β∈都滿足:
(1)Δα,β(Iαβ)?Iα?Cβ,則稱I={Iα|Iα?為C=,Δ,ε)的一個左π-余理想;
證明 僅證明J={Jα|Jα?為H的左-理想的情形,對于J={Jα|Jα?為H的右-理想的情形,類似可證得.
首先由于H為局部有限維的Hopfπ-余代數,故由引理2,H的對偶H0是局部有限維的Hopf-余代數.又由于J={Jα|Jα?為局部有限維的Hopfπ-代數H的左π-理想,故mαβ(Jα?Hβ)?Jαβ.最后由Hopf-余代數H0的結構映射構造過程可知:由于對于任意的α,β∈=.故
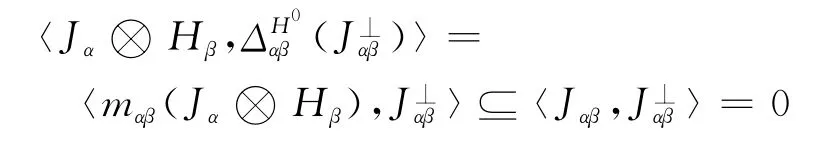
所以
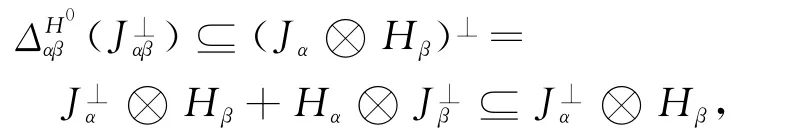
證明 類似定理1可證得.
證明 由定理1和定理2可直接推得.
[1] Virelizier A.Hopf group-coalgebras[J] .Journal of Pure and Applied Algebra,2002(171):75-122.
[2] 顏美玲,李金其.Hopf-代數[J] .龍巖學院學報,2005,23(6):1-3.
[4] Sweedler M E.Hopf algebra[M] .New York:Benjiamin,1969.

