含下有界非線性項(xiàng)的一類特征值問(wèn)題解的存在性
韓開山,劉寶芳
(中北大學(xué)理學(xué)院,山西太原030051)
本文考察下列三階三點(diǎn)非線性特征值問(wèn)題解的存在性與多解性
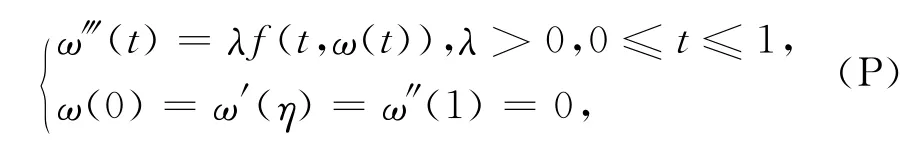
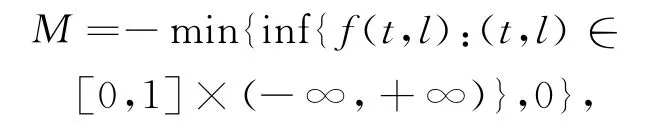
于是M≥0.非線性三階三點(diǎn)邊值問(wèn)題
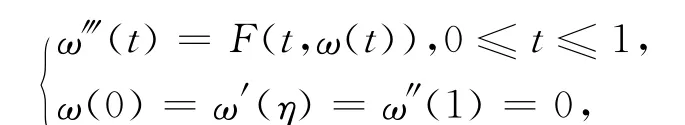
受姚慶六和Henderson等人研究的啟發(fā)[1-3],本文在非線性項(xiàng)f下有界的情況下(因而允許f取負(fù)值),利用錐拉伸與錐壓縮型的Krasnosel′skii不動(dòng)點(diǎn)定理處理三階三點(diǎn)非線性特征值問(wèn)題(P)并獲得一些新的存在性與多解性的結(jié)論.本文主要工作是對(duì)文獻(xiàn)[1] 的結(jié)果進(jìn)行改進(jìn)和推廣,主要思想來(lái)自論文[1-3] .
1 引理
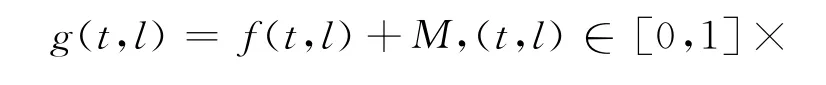
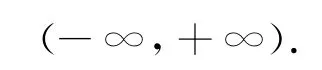
顯然g:[0,1] ×(-∞,+∞)→[0,+∞)連續(xù).
考察三點(diǎn)邊值問(wèn)題
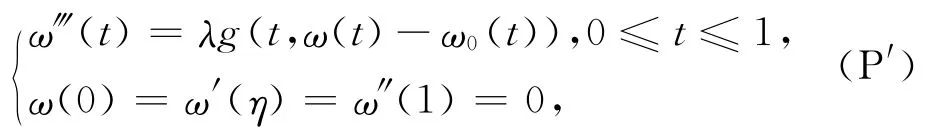
其中ω0(t)=λMt(t2-3t+6η-3η2).注意到
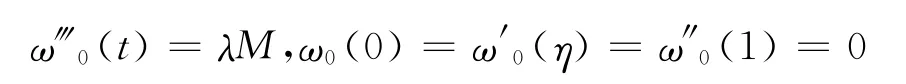
引理1 ω*是問(wèn)題(P)的解當(dāng)且僅當(dāng)=+ω0是問(wèn)題(P′)的解.證明 必要性:設(shè)ω*是問(wèn)題(P)的解,則滿足ω*?(t)=λf(t,ω*(t))且ω*(0)=ω*′(η)=ω*″(1)=0,這樣
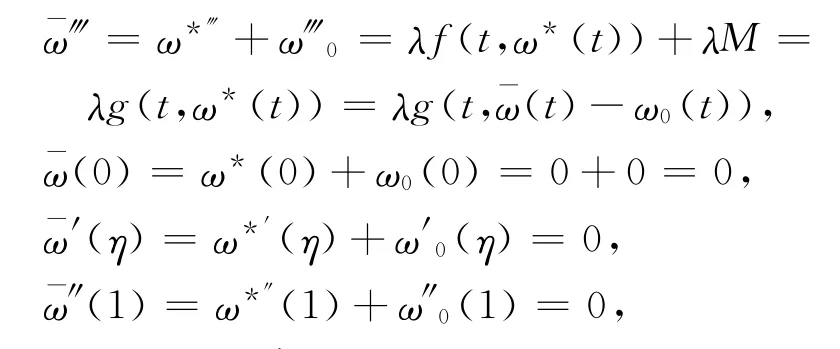
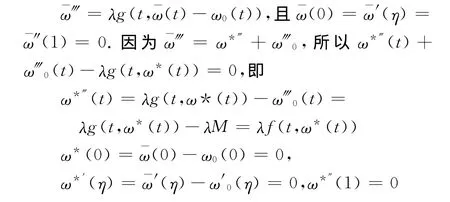
所以ω*是問(wèn)題(P)的解.
設(shè)齊次方程ω?(t)=0,0≤t<1在問(wèn)題(P)中邊界條件下的Green函數(shù)為G(t,s)[4],即
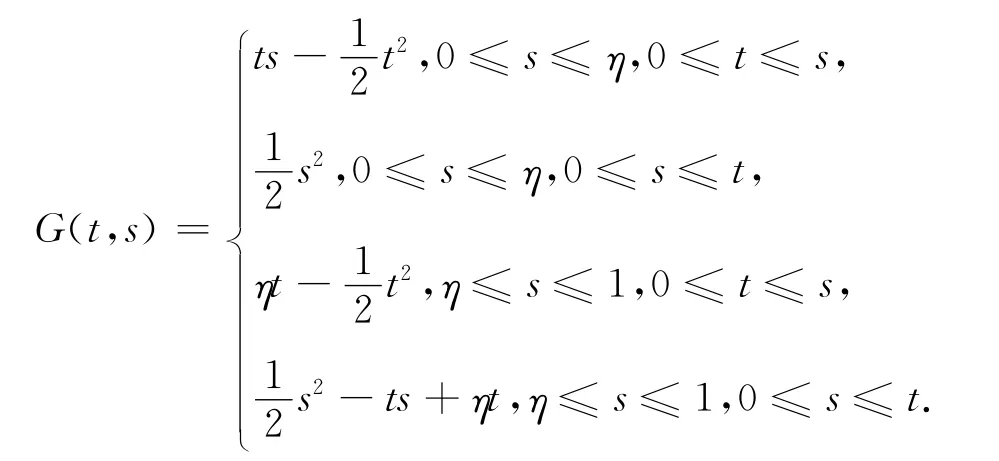
顯然G(t,s)>0,(t,s)∈(0,1)×(0,1).經(jīng)計(jì)算
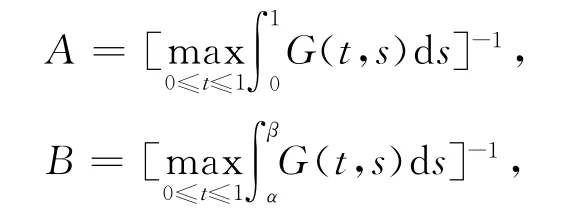
其中
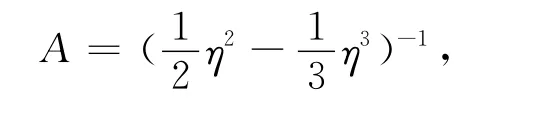
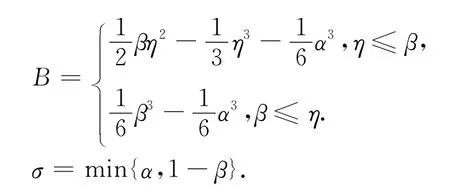
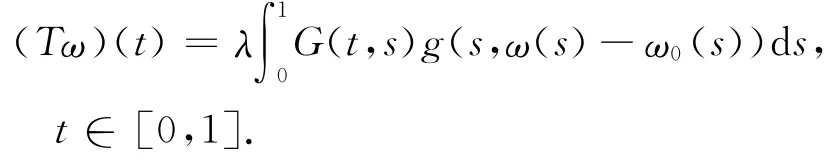
眾所周知,算子T的不動(dòng)點(diǎn)即為問(wèn)題(P′)的解.
引理2 T:K→K是全連續(xù)的.
證明 設(shè)ω∈K,那么Tω∈C([0,1] ,[0,+∞)),因?yàn)椋═ω)?(t)=λg(s,ω(s)-ω0(s))≥0,0≤t≤1,(Tω)″(t)在[0,1] 上是一個(gè)遞增函數(shù),因?yàn)椋═ω)″(1)=0,有(Tω)″(t)≤0,0≤t≤1,因此Tω是一個(gè)凹函數(shù),即對(duì)任意t1,t2,γ∈[0,1] ,
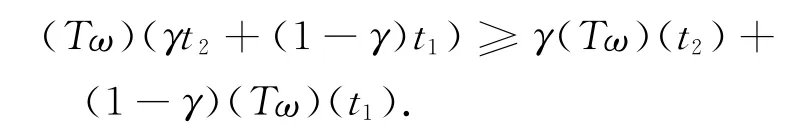
因?yàn)椋═ω)(0)=0,存在t0∈[0,1] ,使得(Tω)(t0)=‖Tω‖.利用Tω的凹性,
若t0=1,可得(Tω)(t)≥‖Tω‖t≥‖Tω‖min{t,1-t},t∈[0,1] ;
從而(Tω)(t)≥‖Tω‖min{t,1-t},t∈[0,1] ,所以(Tω)(t)≥‖Tω‖{t,1-t}=σ‖Tω‖.
從而T:K→K且由Ascoli-Arzela定理可知T是全連續(xù)的.
引理3 (錐拉伸和錐壓縮型的krasnosel′skii不動(dòng)點(diǎn)定理)[5-6]
設(shè)E是Banach空間,K?E是E中的錐,假設(shè)Ω1及Ω2是E的開子集,0∈Ω1,且?Ω2,T:K∩→K是全連續(xù)算子.如果以下兩條件之一成立:
(ⅰ)‖Tu‖≤‖u‖,?u∈K∩?Ω1且‖Tu‖≥‖u‖,?u∈K∩?Ω2;
(ⅱ)‖Tu‖≤‖u‖,?u∈K∩?Ω2且‖Tu‖≥‖u‖,?u∈K∩?Ω1.
對(duì)于l>0,本文采用下列記法:
還需下列極限:
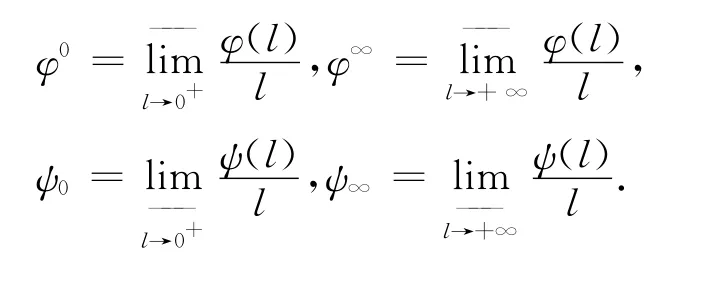
2 主要結(jié)果
下面給出本文的主要結(jié)果并且列出如下假設(shè):
(H1)f(t,ω(t)):[0,1] ×(-∞,+∞)→(-∞,+∞)連續(xù)且下有界,
(H2)M=-min{inf{f(t,l):(t,l)∈[0,1] ×(-∞,+∞)},0},
(H3)ψ∞>0,φ0<∞且<
(H4)φ0>0,ψ∞<∞且<
定理1 假設(shè)(H1)-(H3)成立,則對(duì)任意λ∈,非線性特征值問(wèn)題(P)至少有一個(gè)解.
令Ω1={ω∈K:‖ω‖<R1},當(dāng)ω∈?Ω1,0≤ω(s)≤R1,有
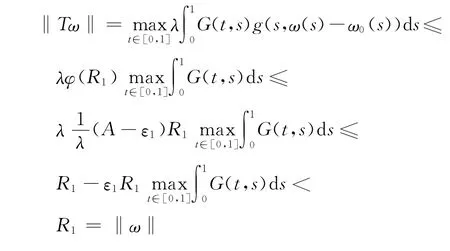
令Ω2={ω∈K:‖ω‖<R2},當(dāng)ω∈?Ω2,σR2≤ω(s)≤R2,α≤t≤β,
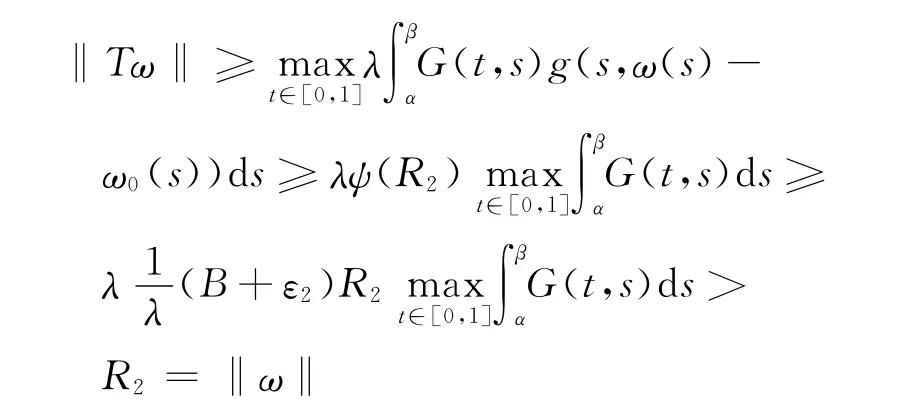
利用引理2及引理3,算子T有一個(gè)不動(dòng)點(diǎn),即問(wèn)題(P′)有一個(gè)解∈K,再根據(jù)引理1知ω*=-ω0為問(wèn)題(P)的解.
定理2 假設(shè)(H1)、(H2)、(H4)成立,則對(duì)任意λ∈,非線性特征值問(wèn)題(P)至少有一個(gè)解.
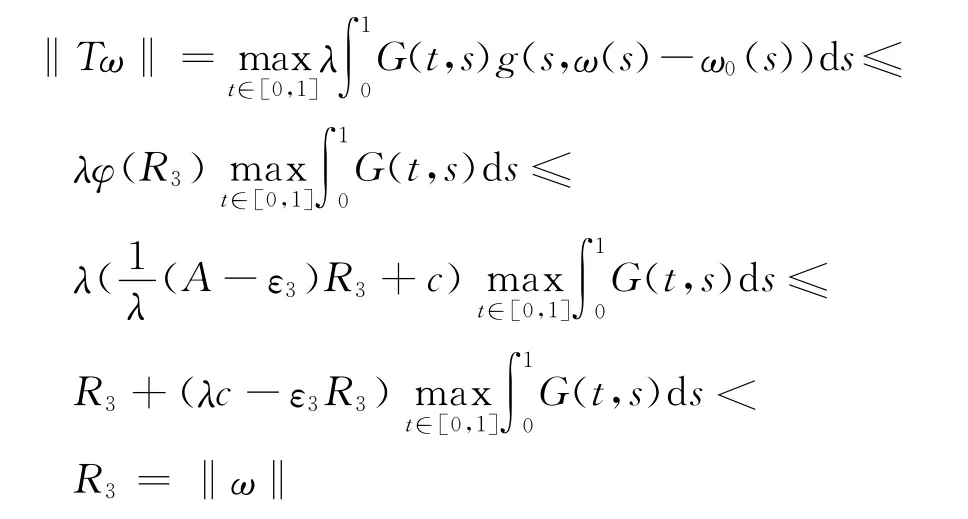
令Ω4={ω∈K:‖ω‖<R4},當(dāng)ω∈?Ω4,σR4≤ω(s)≤R4,α≤t≤β,g(s,ω(s)-ω(s))≥ψ(R)≥R,044
所以
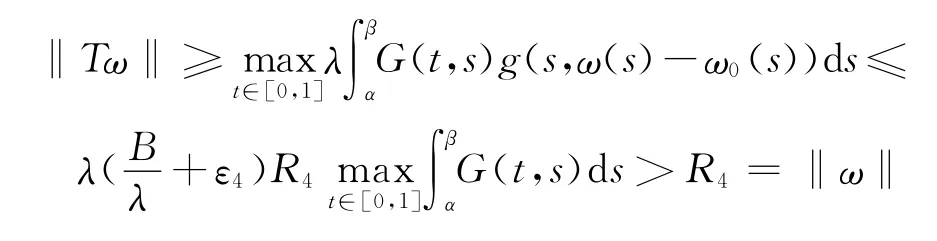
利用引理2及引理3,算子T有一個(gè)不動(dòng)點(diǎn),即問(wèn)題(P′)有一個(gè)解∈K,再根據(jù)引理1知ω*=-ω0為問(wèn)題(P)的解.
當(dāng)λ=1時(shí),有如下結(jié)果:
定理3 假設(shè)(H1)、(H2)成立,且存在兩個(gè)正數(shù)a,b使得φ(a)≤aA,ψ(b)≥bB,則問(wèn)題(P)至少有一個(gè)解ω*滿足ω*+ω0∈K并且min{a,b}≤‖ω*+ω0‖≤max{a,b},此外,若
證明 因?yàn)锳<B,容易看出a≠b,記Ωa={ω∈K:‖ω‖<a},Ωb={ω∈K:‖ω‖<b},如果ω∈?Ωa,則0≤ω(s)≤a,0≤t≤1,于是,0≤g(t,ω(t)-ω0(t))≤φ(a)≤aA,0≤t≤1,則
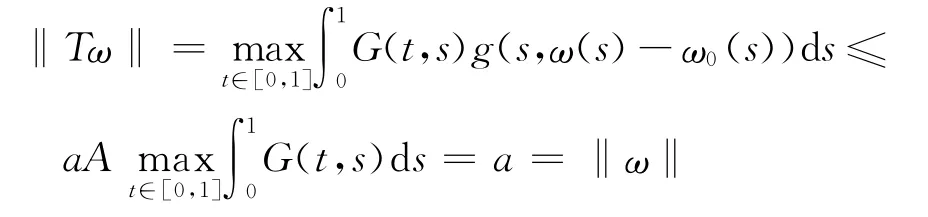
如果ω∈?Ωb,則σb≤ω(s)≤b,α≤t≤β,于是,g(t,ω(t)-ω0(t))≥ψ(b)≥bB,α≤t≤β,則
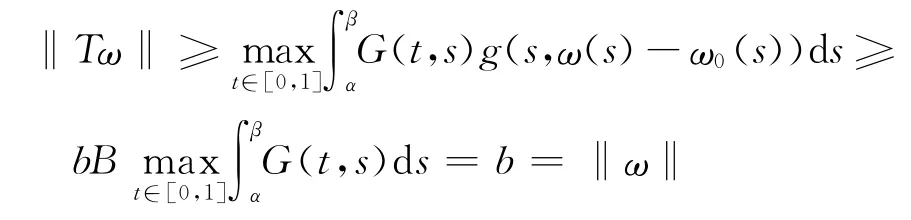
利用引理2及引理3,算子T有一個(gè)不動(dòng)點(diǎn),即問(wèn)題(P′)有一個(gè)解∈K,且a≤‖‖≤b,再根據(jù)引理1我們知ω*=-ω0為問(wèn)題(P)的解.
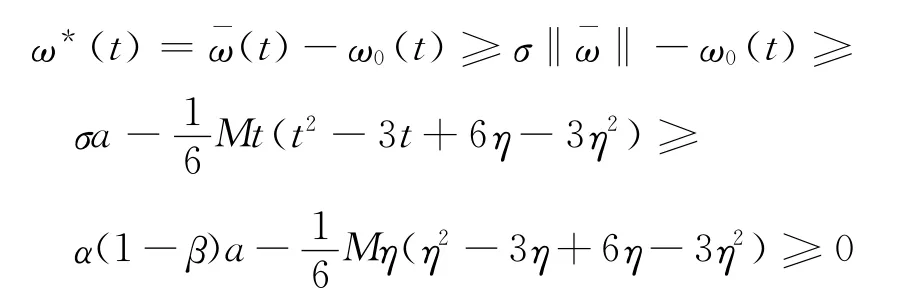
定理得以證明.
定理4 假設(shè)(H1),(H2)成立,且存在三個(gè)正數(shù)a<b<c使得下列條件之一成立:
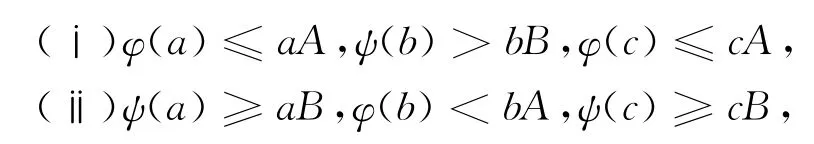
證明 僅證(ⅰ),因?yàn)棣祝海?,+∞)→[0,∞)連續(xù),知存在a<b1<b<b2<c使得ψ(b2)>b2B并且ψ(b1)>b1B,這樣分別對(duì)于{a,b1},{b2,c}使用定理3可推出所需的結(jié)論.
定理5 假設(shè)(H1)、(H2)成立,且存在四個(gè)正數(shù)a<b<c<d使得下列條件之一成立:(ⅰ)φ(a)≤aA,ψ(b)>bB,φ(c)<cA,ψ(d)≥dB,
(ⅱ)ψ(a)≥aB,φ(b)<bA,ψ(c)>cB,φ(d)≤dA
證明 僅證(ⅰ),因?yàn)棣祝海?,+∞)→[0,∞)連續(xù),φ:[0,+∞)→[0,∞)連續(xù),知存在
a<b1<b<b2<c1<c<c2<d使得ψ(b2)>b2B并且ψ(b1)≥b1B,φ(c1)<c1A,φ(c2)≤c2A,這樣分別對(duì)于{a,b1},{b2,c1},{c2,d}使用定理3可推出所需的結(jié)論.
[1] 姚慶六.On the existence of positive solution for a nonlinear third-order three-piont boundary value problem[J] .東北數(shù)學(xué),2003,19(3):244-248.
[2] 姚慶六.含下有界非線性項(xiàng)的一類彈性梁方程解的存在性與與多解性[J] .應(yīng)用數(shù)學(xué)學(xué)報(bào),2004,27(1):117-122.
[3] Henderson J.Positive solutions for nonlinear eigenvalue problems[J] .J.Math.Anal.Appl,1997,208:252-289.
[4] Anderson D.Multiple positive solutions for a three-point boundary value problem[J] .Math.comp.mode,1998,27(6):49-57.
[5] 毛安民,欒世霞.非線性特征值問(wèn)題的正解[J] .?dāng)?shù)學(xué)學(xué)報(bào),2003,24A(2):167-174.
[6] 鐘承奎,范先令,陳文源.非線性泛函分析引論[M] .蘭州:蘭州大學(xué)出版社,1998.

