使用變異系數和Kurtosis系數的雙輔助變量的比估計

盧靜莉

（內蒙古工業大學 理學院，呼和浩特 010051）

0 引言

在抽樣調查中，輔助信息常常被用來提高估計量的精度，當有多個輔助信息可以利用時，估計量的精度會大幅度提高，如何利用多個輔助信息來提高估計的精度成為人們研究的熱點[1～3]。本文擬定義一種使用變異系數和kurtosis系數的雙輔助變量的比估計法，研究這種方法下估計量的均方誤差，證明在一定條件下這種方法下的估計量優于傳統的使用雙輔助信息的比估計量，同時對這些估計量進行比較。

1 已有的一些比估計量

1.1 Sisodia and Dwivedi單輔助變量比估計量[4]

設Y是調查指標，X是輔助信息，當輔助變量X的變異系數Cx已知時，Sisodia and Dwivedi定義的比估計量為

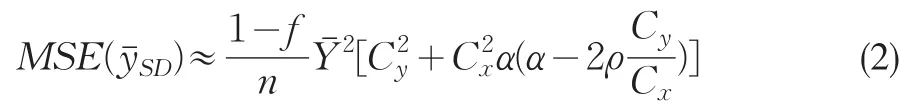
1.2 Upadhyaya and Singh單輔助變量比估計量[5]

當輔助變量X的變異系數Cx和Kurtosis系數β2(x)已知時，Upadhyaya and Singh定義的比估計量為

均方誤差

1.3 傳統的雙輔助變量比估計量[6]

當有兩個輔助信息X1和X2可利用時，定義雙輔助信息的比估計量為

均方誤差

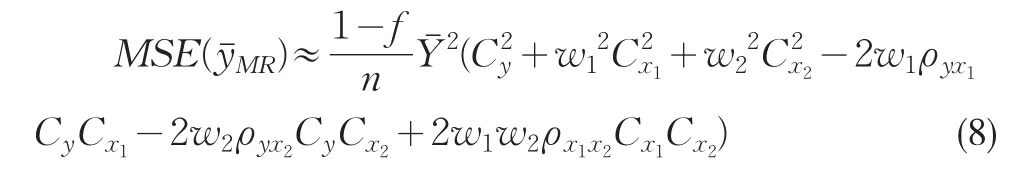
其中，w1,w2是適當選取的權，w1+w2=1；Cy,Cx1和Cx2分別是Y,X1和X2的變異系數；ρyx1,ρyx2,ρx1x2分別是Y與X1，Y與X2，X1與X2的相關系數。

2 使用變異系數和Kurtosis系數的雙輔助變量的比估計

定義1 Y是調查指標，X1,X2是輔助信息，w11,w12,w21,w22,w31,w32是適當選取的權，w11+w12=1，w21+w22=1，w31+w32=1,則的估計量定義為

則均方誤差

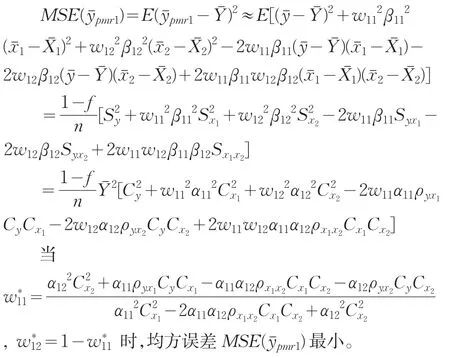
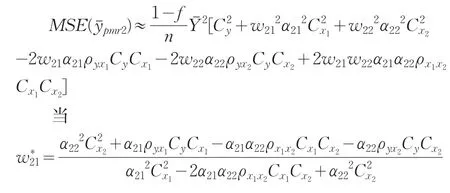
3 效率比較

首先，把使用變異系數和Kurtosis系數的雙輔助變量的比估計量同傳統的雙輔助信息比估計量進行比較，得到如下結論：

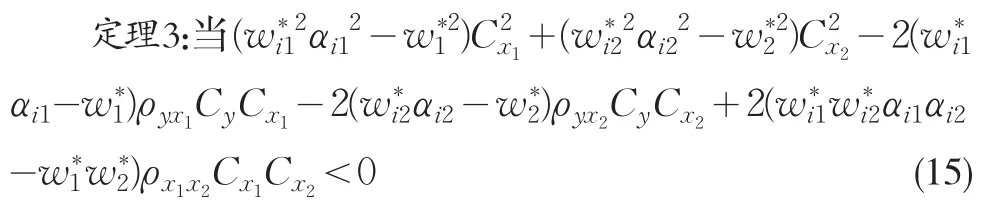
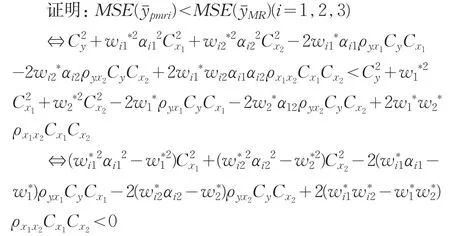
其次,對使用變異系數和Kurtosis系數的雙輔助變量的比估計量的三種估計量進行比較，得到如下結論：

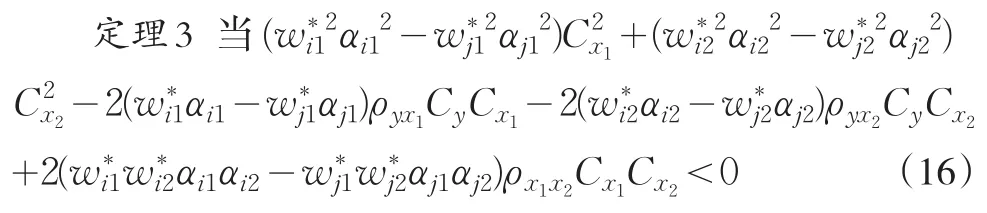
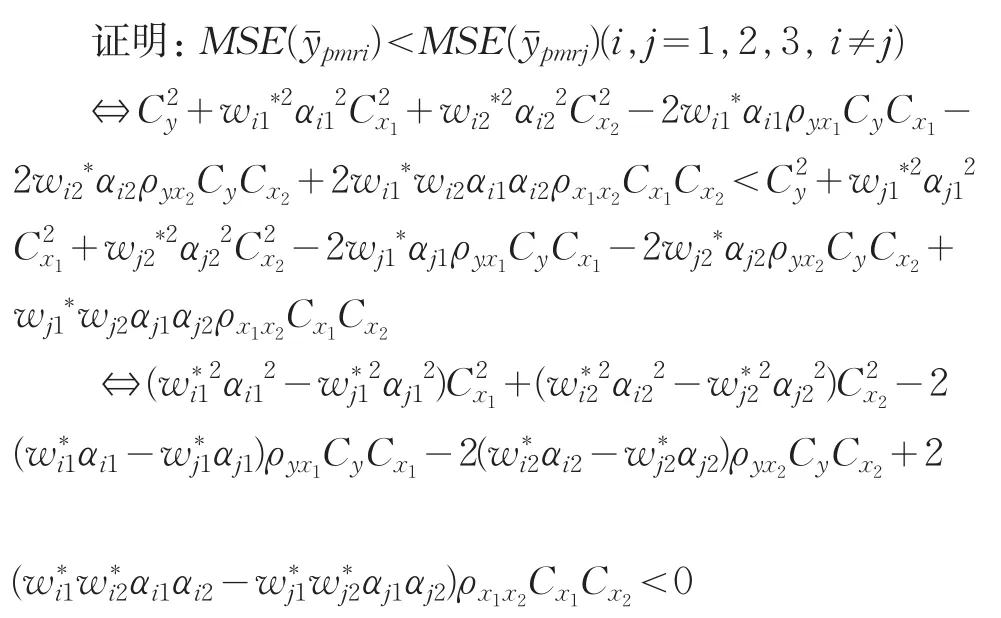
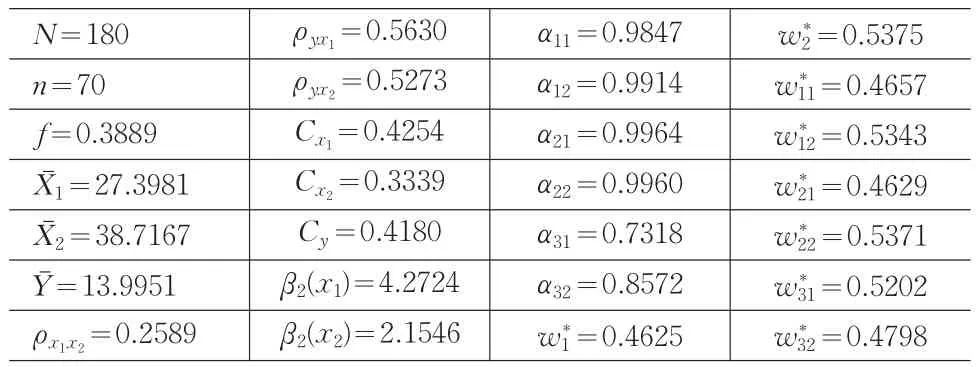
表1 統計數據

4 數值比較

下面以表1中的數據為例來驗證定理2和定理3。

表2 比估計量的均方誤差

從表2中可以看出第一種定義的比估計量是最優的，這是因為當i=1時(15)式及（16）式都得到了滿足

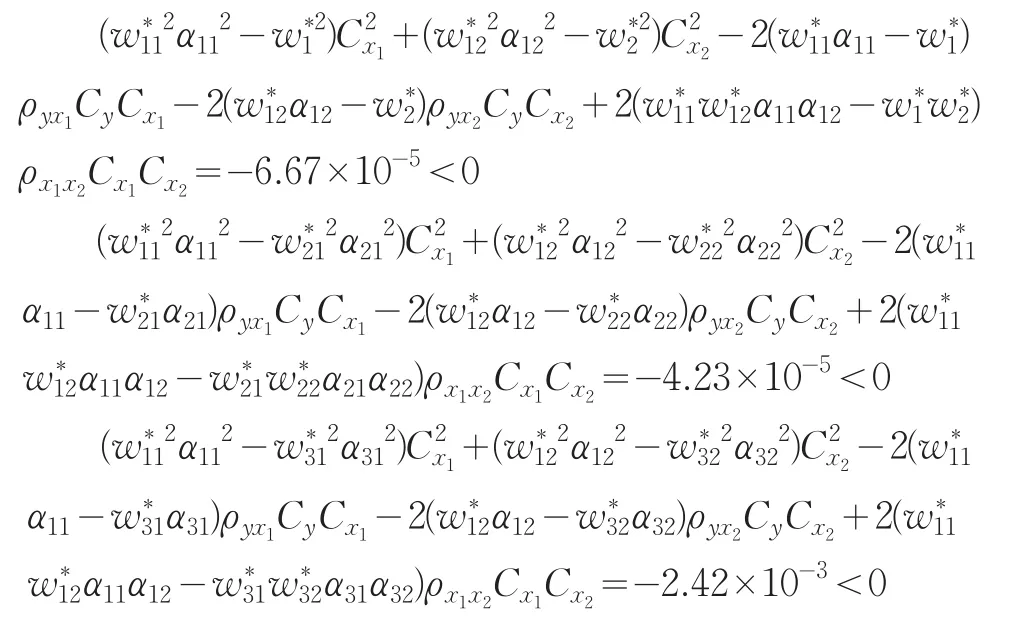
同時從表2還可以看出除了第一種定義的估計量外，第二種定義的估計量也優于傳統的雙輔助信息比估計量。

5 結論

文本定義了三種使用變異系數和Kurtosis系數的雙輔助變量的比估計量，研究了它的均方誤差，并且指出均方誤差最小時權的取值，證明了當滿足一定條件時，新定義的雙輔助信息比估計量優于傳統的雙輔助信息比估計量；同時也得到了這三種估計量一個優于另一個的條件；并且從數值方面得到了驗證。

[1]W.A.Abu-Dayyeh,M.S.Ahmed,R.A.Ahmed,et al.Some Estimators of a Finite Population Mean Using Auxiliary Information[J].Applied Mathematics and Computation,2003,(139).

[2]C.Kadilar,H.Cingi.A Study on the Chain Ratio-type Estimator[J].Hacettepe Journal of Mathematics and Statistics,2003,(32).

[3]C.Kadilar,H.Cingi.A New Estimator Using Two Auxiliary Variables[J].Applied Mathematics and Computation,2005,(162).

[4]B.V.S.Sisodia,V.K.Dwivedi.A Modified Ratio Estimator Using Coef?ficient of Variation of Auxiliary Variable[J].Journal of Indian Society Agricultural Statistics,1981,(33).

[5]L.N.Upadhyaya,H.P.Singh.Use of Transformed Auxiliary Variable in Estimating the Finite Population Mean[J].Biometrical Journal,1999,41(5).

[6]馮士雍，倪加勛，鄒國華.抽樣調查理論與方法[M].北京：中國統計出版社，1998.