基于非對稱信息理論的團購網站盈利模式分析

鄧安平，吳繼飛，趙 康

（重慶郵電大學 經濟管理學院，重慶 400065）

0 引言

隨著互聯網的迅猛發展，電子商務平臺的完善，購物網站的激烈競爭，普通的購物網站已逐漸不能滿足消費群體的心理等方面需求，團購網站作為特殊的購物網站提供低廉的價格應運而生了。2002年，Kaffman將網絡團購定義為：所謂的線上集體購物是指利用網絡聯合有意愿購買的消費者提高對供應商的議價能力，進而以較低廉的價格來購買商品[1]。團購網站將商家與團購聯盟聯系在一起，并與團購聯盟之間進行價格博弈的過程，以期達到自身利益最大化。團購網站在整合供應鏈上游貨物資源過程中，由于存在信息不對稱，商家需要通過一定的機制來激勵團購網站選擇有利于自己的行動以達到更優化的貨物資源整合，因此，研究團購網站的盈利模式——激勵機制問題有非常重要的意義。Krishan S.Anand和Ravi Aron從動態的價格機制出發分析網絡團購存在的基礎，并設立了相關的模型對此來進行研究[2]；趙保國從消費者的角度，考慮了數量價格折扣，構建了虛擬團購網站模型[3]；他們的研究都是基于網站門戶最根本的盈利模式的研究，并未從委托代理關系去探究。與他們的研究不同：本文基于委托代理的關系進行研究團購網站的盈利模式，并考慮現實生活中信息不對稱的情況下商家與團購網站之間的博弈盈利模式分析。以下首先建立優化模型并求解，然后對模型的解進行分析討論，最后通過實例驗證了本文的主要結論。

1 團購網站的委托代理模型

1.1 模型假設

根據委托代理理論以及前述團購網站的特點作如下假設：

（1）假設商家不能觀測到團購網站的努力水平，但是能對團購網站的產出進行核算。

（2）文獻[4]-[5]假設產出函數為常數產出系數的線性函數,文獻[6]假設產出系數與努力水平有關，據前述商家與團購網站的委托代理關系可知團購網站的產出系數會受商家努力水平的影響并非是常數，因此，我們根據文獻[5]、[6]設定的線性產出函數并結合團購網站的特點，假設團購網站的產出函數為：

π=f(xs)xw+ξ,ξ～N(0,σ2)

其中ξ為隨機誤差項，表示外在不可控的因素；xs表示商家的努力水平，具體與商家花在信息共享、培訓、質量指導、協調、管理等方面的人力、物力等耗費有關；xw為團購網站的努力水平，具體可用團購網站在提高自身能力、增加產出等方面的人力、物力等耗費的綜合加權平均值的大小來衡量；f(xs)為團購網站的產出系數，商家的努力水平對團購網站的產出系數起到影響作用，而且f(xs)是關于商家努力水平xs的函數，根據微觀經濟學的原理，f(xs)滿足邊際報酬遞減規律。

（3）文獻[4]—[7]假設委托方為風險中性，代理方為風險規避，但是現實社會中商家與團購網站都是理性經濟人，因此，我們根據文獻[4]—[7]，結合現實社會中商家與團購網站都是理性人，假設商家與團購網站均均是風險規避的，且風險規避不變的特征，假定其效用函數為：

U=-e-ρω

其中，ρ為絕對風險規避量；ω為實際貨幣收入。

（4）根據微觀經濟學的基本原理，結合文獻[13]假設商家的等價努力成本函數為為商家的努力成本系數，αs與商家的能力有關，能力越強，αs越小；同理，團購網站的等價努力成本函數為表示團購網站的努力成本系數，團購網站的努力成本系數與自身能力水平呈負相關性。

（5）為激勵團購網站努力工作，降低自身成本，假定商家與團購網站簽定以下合同：

R(π)=R0+kπ

其中，R(π)為商家支付給團購網站的報酬，R0為商家給予團購網站的固定支付，k為激勵系數，即提成比例。

1.2 建立模型

據前述及假設條件（3）商家與團購網站均是風險規避的，且風險規避不變的特征，不妨令風險規避量分別為ρs，ρw，則商家與團購網站的效用函數分別為：

U(s)=-e-ρsωs，U(w)=-e-ρwωw

ωs，ωw表示商家與團購網站的實際貨幣收益。

根據Arrow-Pratt結論[]1，商家與團購網站經營的風險成本分別為：

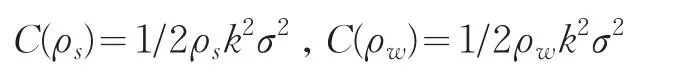
商家與團購網站的實際貨幣收益分別為：

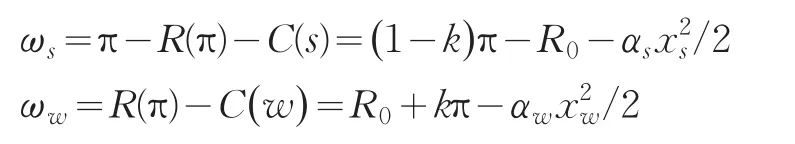
團購網站確定性等價收益為：

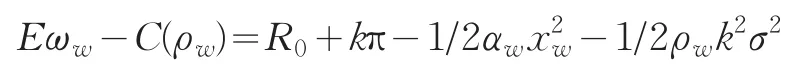
同理，商家的確定性等價收益為：

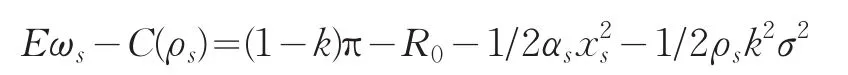
由于團購網站最大化期望效用函數EUw=-Ee-ρwωw等價于最大化確定性收益，因此，我們以確定性收入替代期望效用。不妨設團購網站的保留收入水平為，當確定性等價收益小于時，團購網站接不接受合同。故團購網站參與合作的約束為：

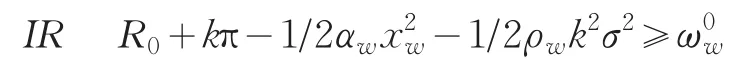
在商家給定團購網站的報酬時，團購網站將選擇最優的努力水平來最大化其確定性等價收益。因此，對于團購網站還必須滿足激勵相容約束條件：

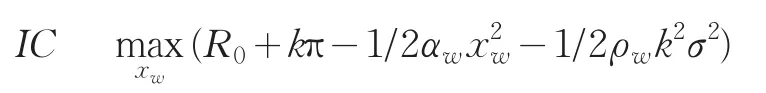
鑒于信息的非對稱，商家不能觀測到團購網站的努力水平，因此，商家必須在激勵團購網站在努力工作的同時實現期望收益的最大化。據前文分析及假設條件，我們建立如下委托代理模型：

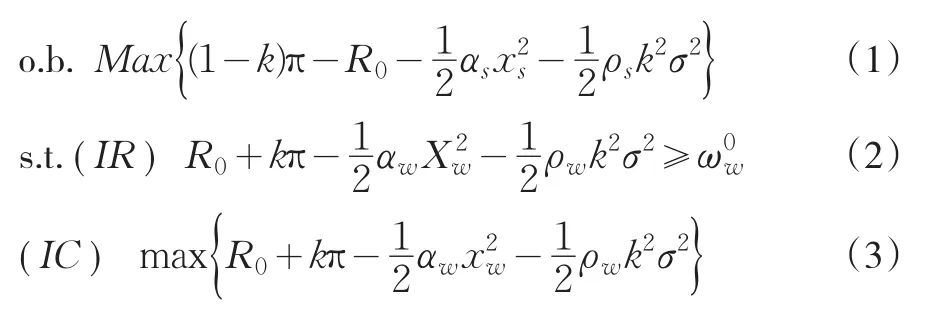
假定團購網站在是否接受合約之間是無差異的，則團購網站總是選擇接受合約；而理性的商家不會給予團購網站更多的支付，所以，在最有情況下，參與約束的（2）式等式成立，結合文獻[8]、[9]，求解可得：

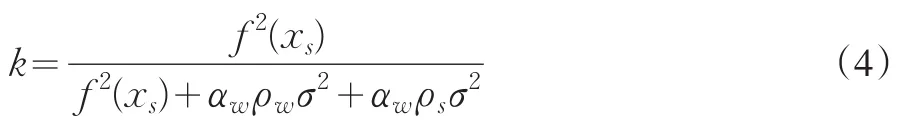
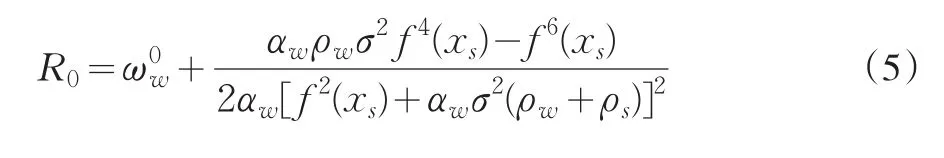
2 模型分析

基于委托代理理論下，商家給予團購網站合理地提成比例（激勵系數）k問題，還需要我們對模型進行進一步的分析：

（1）據（4）式可知，團購網站的提成比例k值大小與f2(xs)成正相關，商家的努力程度越高，給予團購網站的提成比例越大。

（2）據（4）式可知，團購網站的提成比例k值大小與商家的風險規避度ρs成負相關性，商家風險規避度越大，說明商家越害怕風險，則商家給予團購網站的提成比例越小。

當ρs→0時，即商家風險中性，可以解釋為團購網站的提成比例k不受商家的風險影響；當ρs→∞時，即商家風險規避度無窮大，團購網站的提成比例k為0。

（3）據（4）式可知，團購網站的提成比例k值大小與團購網站自身風險規避度成負相關，團購網站的風險規避度越大，說明越害怕風險，則商家給予的提成比例越小。

（4）據（4）式可知，團購網站的提成比例k值大小與團購網站的努力成本系數αw負相關，團購網站的努力成本系數越大，說明團購網站能力越弱，則商家給予能力越弱的團購網站的提成比例越小。

（5）據（4）式可知，團購網站的提成比例k值大小與外生不確定性因素σ成負相關性，外生不確定性因素越多，說明自然社會條件越不穩定，商家給予團購網站的提成比例越小。當σ→0時，k=1，說明不存在外生因素的影響，團購網站的提成比例為1，這種理想狀態在現實社會中是不存在的；當σ→∞時，說明外生不確定因素太大，商家不給予團購網站的提成比例，只給予固定支付。

3 實例分析

為了進一步說明商家如何確定不同情形下給予團購網站的最有報酬及自身的努力水平，我們在這里給出幾種具體情況下的數值算例。根據前述假設（2），不妨設定團購網站的產出系數λ(xs)與商家努力水平xs的函數關系為：

將（6）式帶入（1）（4）（5）式得：

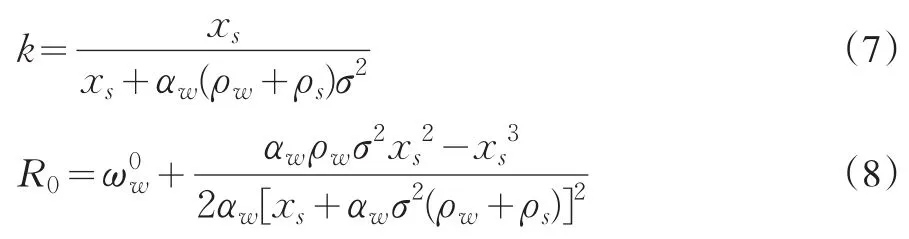
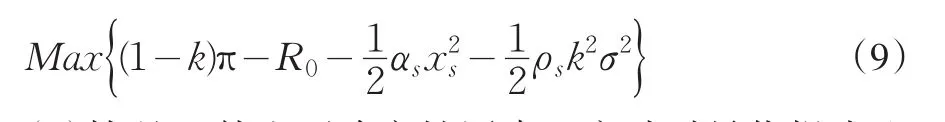
（1）情況1：外生不確定性因素σ變動時最優提成比例k的確定

若ρs=2，ρw=1，xs=64，αw=0.4ωw0=108，分別將其代入（7）（8）（9）式。當σ=15時，R0=109.19，k=19.16% ；當σ=20時，R0=109.66，kσ=20=11.76%＜kσ=15=19.16%。可見，當外生不確定性因素σ越大，說明團購網站外部環境不確定性因素越多，商家給予團購網站的提成比例越小；商家給予團購網站的固定支付分別為109.19和109.66。

（2）情況2：團購網站努力成本系數αw不同時最優提成比例k的確定

若σ=15，ρs=2，ρw=1，xs=64，ωw0=108，將參數代入（7）（8）（9）式。當αw=0.2 時，R0=103.09，k=32.16% ；當αw=0.4時，R0=109.20，k=19.16% ＜k=32.16%。可見，當團購網站努力成本系數增大時，說明團購網站的能力變弱，則商家給予更小的提成比例；商家給予團購網站的固定支付分別為103.09和109.20。

（3）情況3：團購網站風險規避度ρw不同時最優提成比例k的確定

若σ=15，ρs=2，xs=64，αw=0.4ωw0=108，分別 代 入（7）（8）（9）式 。 當ρw=1 時 ，R0=109.20 ，k=19.16%；當ρw=2時，R0=111.30，k=15.09% ＜k=19.16%。可見，當團購網站風險規避度增大時，更不愿意承擔風險，更懼怕風險，商家給予其更小的提成比例；商家給予團購網站的最優固定支付分別為109.20和111.30。

（4）情況4：商家風險規避度ρs不同時最優提成比例k的確定

若σ=15，ρw=1，xs=64，αw=0.4ωw0=108，代入（7）（8）（9）式。當ρs=1時，R0=110.24，k=26.23%；當ρs=2時，R0=109.19，k=19.16%＜k=26.23%。可見，當商家風險規避度增大時，說明商家更懼怕風險，則商家給予團購網站更小的提成比例；商家給予團購網站的最優固定支付分別為110.24和109.19。

（5）情況5：商家最優努力水平的確定

將（7）式變形得：

若σ=15，ρw=1，ρs=2，αw=0.4 ，αs=0.6，將參數分別代入（10）式，則xs=47.65，可見商家在給定的參數情況下的最優努力水平為47.65。

4 結語

以上我們根據商家與團購網站的委托代理關系，考慮了商家的努力水平對團購網站努力產出系數的影響并基于一對一的關系進行研究，從而給出了團購網站一種新型的盈利模式。分析了團購網站最優的提成比例，并得出了以下結論：商家自身能力越強，努力水平就會越高，給予團購網站的提成比例越大；商家與團購網站的風險規避度越大，給予團購網站的提成比例越小；團購網站的能力越強，努力成本系數就越小，商家給予的提成比例越大的激勵。最后我們進行了實例分析進一步的說明了商家給予團購網站的最優提成比例（激勵系數），最優固定支付及最優努力水平的確定方法。本文的研究是以商家與團購網站的一對一的委托代理關系為基礎的，未考慮一個商家對應多個團購網站的情形。商家與多個團購網站情形下的激勵機制將是我們下一步的研究目標。

[1]Kaffman，R.J,B.Wang.Bid Together,Buy Together：On the Efficacy of Troup-buying Business Models in Internet-based Selling[A].In P.B.Lowry,J.O.Cherrington,and R.R.Watson(Eds.).Handbook of Electron?icCommerce in Business and Society[M].Boca Raton,FL:CRC Press,2002.

[2]Kauffmaa,R.J,Wang,B.New Buyers’Arrival under Dynamic Pricing Market Microstructure:The Case of Group-Buying Discounts on the Internet[J].Joumal of Management Information System,2001,18.

[3]趙保國.個人消費者網絡虛擬團購模型構建及優化[J].中央財經大學學報，2005，（11）.

[4]劉志學，許澤勇.基于非對稱信息理論的第三方物流合作博弈分析[J].中國管理科學，2003，11(5).

[5]曹玉貴.工程監理制度下的委托代理分析[J].系統工程，2005,23（1）.

[6]王勇，羅富碧.第四方物流努力水平影響的物流分包激勵機制研究[J].中國管理科學，2006，14(2).

[7]劉元元，李幫義.基于委托代理的信息共享激勵機制研究[J].統計與決策，2009，（8）.

[8]Arrow K.Essays in the Theory of Risk Bearing[M].Chicago:Markham,1970.

[9]Holmstrom Bengt,Milgrom Paul.Aggregation and Linearity in the Pro?vision of Intertemporal Incentives[J].Econometrica,1987,55(2).