從一道電磁感應問題的幾種解法談平均值

王麗軍

（北京師大良鄉附中，北京 102488）

電磁感應的問題中有一道比較常見的題.如圖1（甲）所示，光滑且足夠長的平行金屬導軌MN、PQ固定在同一水平面上，兩導軌間距L＝0.5m，電阻R＝0.4Ω，導軌上停放一質量m＝0.1kg，電阻r＝0.1Ω的金屬桿，導軌電阻不計，整個裝置處于磁感應強度B＝0.5T的勻強磁場中，方向豎直向下，現用一外力F沿水平方向拉桿，使之由靜止開始做勻加速運動，若理想電壓表示數u隨時間關系如圖1（乙）所示.

（1）求金屬桿運動的加速度大?。?/p>

（2）求第3秒末拉力的功率；

（3）若在第4秒末撤去外力F，則金屬桿還能運動多遠？

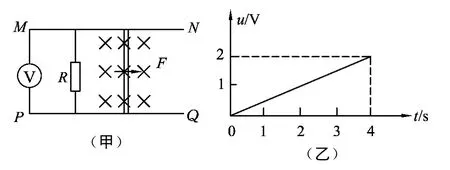
圖1

前兩問的比較簡單在此不再贅述，只分析第三問.

過程分析1：根據前兩問可以求出4s末金屬桿的速度是v0＝10m／s，在撤去外力后，金屬桿只受方向向左的安培力，金屬桿將向右做減速運動直到靜止.

在這個過程中，金屬桿由于切割磁感線產生感應電動勢為E＝BLv，回路中的感應電流為金屬桿受到的安培力為F＝BIL，

可見隨著金屬桿速度的減小，安培力變小，加速度變小，速度隨時間的變化不是均勻的（速度時間圖像如圖2所示），安培力隨時間的變化也不是均勻的，所以這個過程中安培力對時間的平均值，其中F0是撤去外力瞬間的安培力.

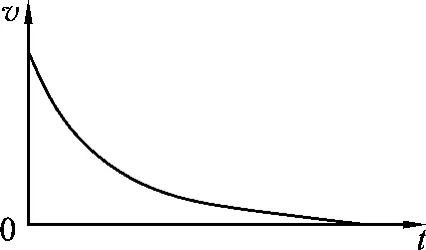
圖2

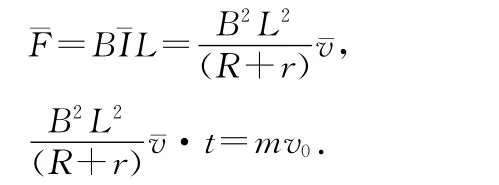
金屬桿運動的距離x＝ˉv·t，代入數據得x＝8m.

解法2：根據動量定理有ˉF·t＝mv0，其中

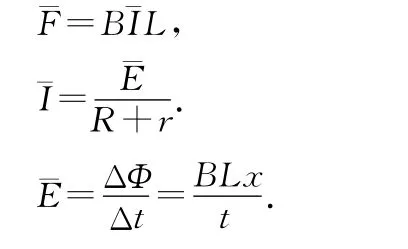
注意：上述兩種解法中的平均值均為對時間的平均值.安培力對時間的平均值

過程分析2：通過上面的分析可知，由于速度隨時間不是均勻變化所以導致感應電動勢、感應電流、安培力隨時間都不是均勻變化，那么速度隨位移的變化是否是均勻的呢？

假設經過一段時間金屬桿的速度從v0減速到v，金屬桿的位移為x.

根據類似解法1和解法2的推導過程可知

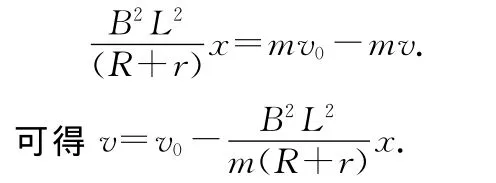
可以看出速度隨位移的變化是線性變化，變化關系如圖3.

即感應電動勢、感應電流、安培力隨位移均勻變化，此過程中安培力對位移的平均值

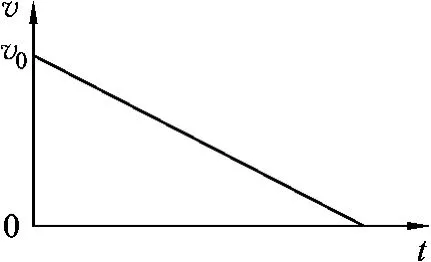
圖3

注意：上述三種解法中有兩個平均值，這兩個平均值的平均的意義是不同的.

小結：關于兩個平均值，一般說來，一個隨時間變化的作用力F（t）作用在質量為m的物體上，經過一段時間t，物體速度從v1變化為v2.根據動量定理，有，則

同時，這個作用力也是隨位移s而變化的，可記作F（s），在速度從v1變化為v2的過程中，發生位移s.根據動能定理，有

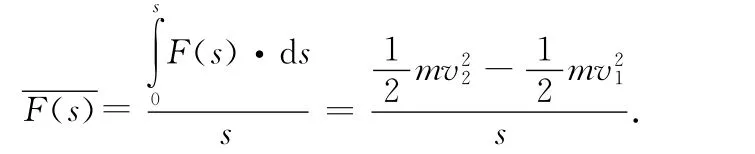
前者稱為作用力對時間的平均值，后者稱為作用力對空間的平均值，一般情況下，二者并不相等在特殊情況下，滿足一定條件，二者可以相等.

所謂“當作恒力處理”，就是把一個變力作用的過程等效為大小等于它的平均力的恒力作用的過程，這里涉及到是哪個平均力的問題.應用動量定理應該是指對時間的平均力，應用動能定理應是指對位移的平均力，而同一個變力對時間的平均與對空間位移的平均一般不相等，一定要區分清楚.

除了上面的3種解法外還可以用積分的辦法.

解法4：設某時刻金屬桿的速度為v，經過很短的時間dt，金屬桿的位移為dx，有

設初速度方向為正，有

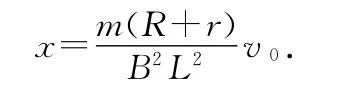
代入數據得x＝8m.

一般情況下，當我們說某個量的平均值，而沒有說明是對什么的平均時，我們就默認為是對時間的平均值，例如我們說的“平均速度”、“平均功率”等等，都是指的對時間的平均值，也就是說，當我們說某個物理量對時間的平均值時，可以省略“對時間”這三個字.

同樣，當我們要求某個過程中的平均作用力時，我們要理解為是對時間的平均，即而不能理解為后者必須稱為“求這個過程中對空間位移的平均作用力”.當我們運用動量定理而求得的平均作用力是對時間的平均力，而我們運用動能定理求得的平均作用力則是對空間位移的平均力.