剩余類環(huán)Z/(pn)上若干類單圈多項式構造
游 偉 戚文峰
(解放軍信息工程大學 鄭州 450002)
1 引言
若f(x)是一個整系數(shù)多項式,當x通過模m的一個完全剩余系時,f(x)也通過模m的一個完全剩余系,則稱f(x)是模m的一個置換多項式。關于置換多項式的研究結果非常多,可參考文獻[1-7]。引起置換多項式迅速發(fā)展的一個主要原因是它已逐漸在數(shù)論,組合論,密碼系統(tǒng)等領域中得到應用。事實上,著名公鑰密碼體制 RSA[8]和分組密碼算法 RC6[9]就是其中的兩個應用。
本文研究的是一類特殊的置換多項式,即剩余類環(huán)上的單圈多項式(見定義 1)。單圈多項式在密碼學的眾多領域都有重要應用。例如,在偽隨機數(shù)發(fā)生器[10]的理論中,狀態(tài)轉移函數(shù)必須提供偽隨機性,特別地,它必須保證狀態(tài)序列的元素分布和周期。為了達到這個目的,我們可以選擇單圈多項式作為狀態(tài)轉移函數(shù),這樣就可以保證狀態(tài)序列達到最大周期并且其元素滿足嚴格一致分布。事實上,經(jīng)典的線性同余發(fā)生器使用的即是一次單圈多項式,它的優(yōu)勢是實現(xiàn)速度快,但弱點是結構過于簡單。本文的目標是構造任意次數(shù)的單圈多項式,這樣就可以利用高次單圈多項式來產(chǎn)生非線性同余發(fā)生器以取代線性同余發(fā)生器。偽隨機數(shù)在包括仿真,抽樣,數(shù)值分析,公鑰密碼算法設計等眾多領域中都有著不同形式的應用。另外,單圈多項式還可以用來構造拉丁方。拉丁方的應用也是極其廣泛的。例如,在保密通信網(wǎng)絡中用來做口令的分發(fā);以及在某些密碼算法的設計中作為多重置換來使用。
Knuth[11]給出了剩余類環(huán)Z/(m)上的所有一次和二次單圈多項式的構造。Larin[12]和 Durand等[13]則分別給出了Z/(2n)和Z/(3n)上任意次單圈多項式的全部構造。然而,對于一般的素數(shù)p,關于Z/(pn)上單圈多項式的構造目前還沒有任何結果。其實,這也并不奇怪,因為即使是有限域Z/(p)上置換多項式的構造都是極其有限的。
本文通過刻畫多項式的系數(shù)給出了Z/(pn)(p≥5)上若干類單圈多項式的構造。由于Z/(pn)上單圈多項式的構造可以歸結到Z/(p2)上,本文首先通過刻畫系數(shù)滿足的條件給出了Z/(5)上任意次單圈多項式的構造,并在其基礎上給出了Z/(52)上 6 次單圈多項式的全部構造。另外,本文還給出了Z/(p2)上 (p-1) 次單圈多項式的部分構造。
2 基礎知識
定義1[12]設f(x)∈Z[x],m≥ 2 是正整數(shù),若遞歸序列ui+1=f(ui)(modm) 的周期達到m,則稱f(x)為剩余類環(huán)Z/(m)上的單圈多項式。
引理1[12]設n≥2,若多項式f(x)∈Z[x]在Z/(pn)上是單圈,則f(x)在Z/(pn-1)上也是單圈。
引理2[12]設p為素數(shù),若多項式f(x)∈Z[x]在Z/(p3)上是單圈,則對任意正整數(shù)n,f(x)在Z/(pn)上都是單圈;特別地,當p?{2, 3}時,若多項式f(x)∈Z[x]在Z/(p2)上是單圈,則對任意正整數(shù)n,f(x)在Z/(pn)上都是單圈。
注 1:由引理 1 和引理 2 可知,當p≥5 時,f(x)在Z/(pn)(n≥2) 上是單圈當且僅當f(x)在Z/(p2)上是單圈。因此,當p≥5時,對Z/(pn)(n≥2) 上單圈多項式的研究都可以歸結到Z/(p2) 上。

下面的引理刻畫了Z/(p)與Z/(p2)上的單圈多項式所滿足條件之間的聯(lián)系。
引理3[13]多項式f(x)∈Z[x],若f(x)在Z/(p)上是單圈,則下面的3個條件是等價的。(1)f(x) 在Z/(p2)上是單圈;(2)對任意x∈Z,fp(x)-x≠0(modp2),并且 (fp)'(x)≡1(modp); (3)存在x∈Z,滿足fp(x)-x≠0(modp2),并且 (fp)'(x)≡1(modp)。
注2:由引理 3 可知,若f(x)在Z/(p)上是單圈,則f(x)在Z/(p2)上也是單圈 ?fp(0) ≠ 0(modp2),并且 (f p)′(0)≡ 1(modp)。
3 Z/(5)上單圈多項式的系數(shù)刻畫
3.1 常數(shù)項為 1 的情形
定理1設f(x)=adxd+ad-1xd-1+…+a1x+1∈Z[x],則f(x)在Z/(5)上是單圈當且僅當A0,A1,A2,A3滿足表1中條件之一。

表1 f(x)在Z/(5)上是單圈的條件
證明因為f(x)=adxd+ad-1xd-1+…+a1x+1,所以

若f(x)在Z/(5)上要構成單圈,則f(1)=1+A0+A1+A2+A3≠ 0 或 1(mod 5),從而有A0+A1+A2+A3≡1, 2或3 (mod 5)。下面分情形討論:
(1)當A0+A1+A2+A3≡ 1(mod5),此時,f(x)在Z/(5)上是單圈當且僅當

連同f(0)=1和f(1)≡2(mod 5),分別求解上述兩個同余方程組可得(A0,A1,A2,A3)≡(0,1,0,0)或(0,4,4,3)·(mod 5)。
(2)當A0+A1+A2+A3≡2(mod 5),同理得f(x)在Z/(5)上是單圈當且僅當(A0,A1,A2,A3)≡(0,1,3,3)或(0,1,4,2)(mod 5)。
(3)當A0+A1+A2+A3≡3(mod 5),同理得f(x)在Z/(5)上是單圈當且僅當(A0,A1,A2,A3)≡(0,4,2,2)或(0,0,0,3) (mod 5)。 證畢
3.2 常數(shù)項不為 1 的情形




表2 g(x)在Z/(5)上是單圈的條件
4 Z/(52)上 6 次單圈多項式的全部構造
4.1 常數(shù)項為 1 的情形
引理4若f(x)在Z/(5)上是單圈,則(f5)′(0)≡a1[(D1+D3)2-(D0+D2)2][(D1-D3)2-(2D2+3D0)2](mod 5)。
證明 因為fk(x)=f(fk-1(x)),所以 (fk)′(x)=f′(fk-1(x))·(fk-1)′(x),故有(f5)′(x)=f′(f4(x))·(f4)′·(x) = … =f′(f4(x)) ·f′(f3(x)) ·f′(f2(x)) ·f′(f(x))·f′(x)。又f(x)在Z/(5)上是單圈,從而對任意x∈Z,有(f5)′(x)≡f′(0)f′(1)f′(2)f′(3)f′(4)(mod 5)。另外

因此(f5)′(0)≡a1[(D1+D3)2-(D0+D2)2][(D1-D3)2-(2D2+3D0)2](mod 5)。 證畢
引理5f(x)如上,對任意素數(shù)p和正整數(shù)k,若fk(0)≡c(modp), 0 ≤c≤p-1,則fk+1(0)≡f(c)+f'(c)(fk(0)-c)(modp2)。
證明 因為fk(0)≡c(modp), 0 ≤c≤p-1,所以fk(0)-c≡0(modp)。則有

注 3:若(A0,A1,A2,A3)≡(0,1,0,0)(mod 5),則由式(1)可知f(0)=1,f2(0)≡2(mod 5),f3(0)≡3·(mod 5),f4(0)≡-1 (mod 5)。
由引理5通過迭代可得

定理2設f(x) =a6x6+a5x5+a4x4+a3x3+a2x2+a1x+1∈Z[x],則f(x)在Z/(52)上是單圈當且僅當a1≡1(mod 5),a2≡a3≡a5≡a6≡0 (mod 5),a4≡0·(mod 5)且a4≠ 5(mod 52)。
證明 由定理 1 及注 2 可知,若f(x)在Z/(5)上是單圈,即A0,A1,A2,A3滿足表1中條件(I)-條件(VI)中的某一個,則f(x)在Z/(52)上是單圈當且僅當 (f5)′(0)≡1(mod 5),及f5(0)≠0(mod 52)。
由Ai和Di的定義易得

下面分情況進行討論:
(1)當 (A0,A1,A2,A3)≡(0,1,0,0)(mod 5),由式(4)可得D0≡0(mod 5),D1≡a1(mod 5),D2≡a2(mod 5),D3≡0(mod 5)。

由此可知,為了給出f(x)在Z/(52)上是單圈的充要條件,我們只需說明當條件式(5)滿足時,f5(0) ≠ 0·(mod 52) 當且僅當a4≠ 5(mod 52)。
當條件式(5)滿足時,由式(2)和式(4)可得f′(2)≡a1+2a2≡1(mod 5),f'(3)≡a1+3a2≡1(mod 5),f'( 4 )≡a1+4a2≡1(mod 5)。
另外,由式(3)可得
f5(0)≡f(-1)+f'(4)(f(3)+1)+f'(4)f'(3)(f(2)-3)+f'( 4 )f'(3)f'(2)(f(1)-2)(mod 52)≡f(-1)+(f(3)+1)+(f(2)-3)+(f(1)-2)(mod 52)≡5a1+15a2+10a3+24a4+20a6(mod 52)≡5-a4(mod 52)
因此,當條件式 (5) 滿足時,f5(0)≠0(mod 52) 當且僅當a4≠5(mod 52)。故在此情形下f(x)在Z/(52)上是單圈當且僅當a1≡1(mod 5),a2≡a3≡a5≡a6≡0 (mod 5),a4≡0 (mod 5)且a4≠ 5(mod 52)。
(2)當(A0,A1,A2,A3)≡(0,4,4,3) (mod 5),由式(4)可得D0≡0 (mod 5),D1≡a1(mod 5),D2≡a2-1·(mod 5),D3≡ -1(mod 5)。
由引理 4 可知(f5)′(0)≡a1[(a1-1)2-(a2- 1)2][(a1+ 1)2+(a2-1)2](mod 5)。
(3)當(A0,A1,A2,A3)≡(0,1,3,3)(mod 5),同理得(f5)′(0)≡a1[(a1- 1)2- (a2- 2)2][(a1+ 1)2+ (a2- 2)2]·(mod 5)。
(4)當(A0,A1,A2,A3)≡(0,1,4,2) (mod 5),同理得(f5)′(0)≡a1[(a1+ 1)2-(a2- 1)2][(a1-1)2+(a2- 1)2]·(mod 5)。
(5)當(A0,A1,A2,A3)≡(0,4,2,2) (mod 5),同理得(f5)′(0)≡a1[(a1+ 1)2-(a2+ 2)2][(a1-1)2+(a2+2)2]·(mod 5)。

在情況(2)- 情況(6)中,遍歷a1和a2的所有取值,易知 (f5)′(0) ≠ 1(mod 5)。這意味著在這些情況下f(x)在Z/(52)上都不可能構成單圈。 證畢
4.2 常數(shù)項不為 1 的情形
推論2設g(x)=a6x6+a5x5+a4x4+a3x3+a2x2+a1x+a0∈Z[x],則g(x)在Z/(52)上是單圈當且僅當a1≡1(mod 5),a2≡a3≡a4≡a5≡a6≡0(mod 5),a0≠0(mod 5)且a0≠(a4/5)(mod 5)。

5 Z/(p2)上(p-1)次單圈多項式的部分構造
引理6設素數(shù)p>3,則

證明因為有限域Z/(p)中的所有非零元素構成乘法循環(huán)群,設=〈g〉。所以
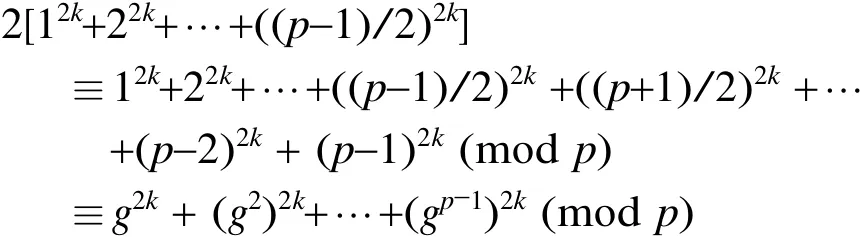


當k= (p-1)/2 時,由歐拉定理可知


證明首先,因為a1≡1 (modp),a2≡a3≡…≡ap-2≡ap-1≡0 (modp),所以f(x)≡x+1(modp)。顯然f(x)在Z/(p)上是單圈。另外,f′(x)=(p-1)ap-1xp-2+ (p-2)ap-2xp-3+…+ 2a2x+a1,因此可得f′(x)≡a1≡1(modp)。
其次,因為f(x)在Z/(p)上是單圈,類似引理4的證明可得(fp)'( 0 )≡f'( 0 )f'( 1 )f'( 2 )…f'(p-1)(modp)≡1(modp)。
最后,因為f(x)≡x+1(modp),由引理5可得

由引理 6和a1≡1(modp),a2≡a3≡…≡ap-2≡ap-1≡0(modp),有f p(0)≡2ap-1(p-1)/2+p(modp2)≡p-ap-1≠0 (modp2)。由注 2 可知,f(x)在Z/(p2)上是單圈。 證畢
6 結束語
目前,只有p=2,3 時,針對剩余類環(huán)Z/(pn)上單圈多項式的研究才全部得以解決。本文對Z/(5)上的任意次單圈多項式進行了完整的系數(shù)刻畫,進一步,對Z/(52)上的 6 次單圈多項式進行了完整的系數(shù)刻畫;另外,本文給出了Z/(p2)(p>3)上的(p-1)次單圈多項式的部分構造。我們下一步的工作有兩個方向:第一,對Z/(p)(p>5)上的單圈多項式進行完整的系數(shù)刻畫;第二,對Z/(p2)(p>3)上的任意次單圈多項式進行完整的系數(shù)刻畫。
[1]Rivest R L. Permutation polynomials modulo 2w.Finite Fields and Their Applications, 2001, 7(2): 287-292.
[2]Weng Guo-biao and Dong Chao-ping. A note on permutation polynomials overZ/nZ.IEEE Transactions on Information Theory, 2008, 54(9): 4388-4390.
[3]Coulter R, Henderson M, and Matthews R. A note on constructing permutation polynomials.Finite Fields and Their Applications, 2009, 15(5): 553-557.
[4]Ostafe A. Multivariate permutation polynomial systems and nonlinear pseudorandom number generators.Finite Fields and Their Applications, 2010, 16(3): 144-154.
[5]Li Ji-you, Chandler D B, and Xiang Qing. Permutation polynomials of degree 6 or 7 over finite fields of characteristic 2.Finite Fields and Their Applications, 2010, 16(6): 406-419.
[6]Akbary A, Ghioca D, and Wang Qiang. On constructing permutations of finite fields.Finite Fields and Their Applications, 2011, 17(1): 51-67.
[7]Marcos J E. Specific permutation polynomials over finite fields.Finite Fields and Their Applications, 2011, 17(2):105-112.
[8]Rivest R L, Shamir A, and Adleman L M. A method for obtaining digital signatures and public-key cryptosystems.Communications of the ACM, 1978, 21(2): 120-126.
[9]Rivest R L, Robshaw M J B, Sidney R,et al.. The RC6 block cipher. http://theory.lcs.mit.edu/~rivest/rc6.pdf, 1998.
[10]Anashin V and Khrennikov A. De Gruyter Expositions in Mathematics. Berlin: Walter de Gruyter, 2009, Vol.49:Applied Algebraic Dynamics.
[11]Knuth D E. The Art of Computer Programming. Reading,MA: Addison-Wesley Publ. Co, 1998, Vol.2: Seminumerical Algorithms (3rd Edition).
[12]Larin M V. Transitive polynomial transformations of residue class rings.Discrete Mathematics and Applications, 2002,12(2): 127-140.
[13]Durand F and Paccaut F. Minimal polynomial dynamics on the set of 3-adic integers.Bulletin of the London Mathematical Society, 2009, 41(2): 302-314.

