裝有軟鋼阻尼器鋼框架地震作用下的仿真分析

聞 輝

(中冶華天工程技術有限公司，江蘇南京 210019)

0 引言

對于結構在地震過程中的動力反應可以通過數值方法求解二階微分方程來求得，實際上，對于任何一個二階動力系統，可以將其看成一個輸入—輸出系統。這樣可以通過MATLAB語言中的Simulink工具箱對該系統進行動態仿真。采用動態仿真計算可以避免繁雜的程序編制，同時將地震過程中的結構當作控制系統分析，概念清楚，易于理解[1]。

本文以裝有軟鋼阻尼器的被動控制結構為例，對結構的動力反應進行動態仿真分析。

1 軟鋼阻尼器的等價線性化

為了便于使用Simulink工具箱對受控結構進行動力仿真，需要對軟鋼阻尼器非線性力進行等價線性化處理。

首先以單自由度體系為例來說明等價線性化的原則。由動力學知識可知，在地震作用下單自由度非線性結構體系的動力方程可表示為:

其中，m為體系的質量;x(t)分別為體系相對于地面的水平位移、速度、加速度為地面運動水平加速度;分別為非線性阻尼力和非線性恢復力。

設與方程(1)等效的線性方程為:

其中，ce，ke分別為等效線性阻尼系數和等效線性剛度系數。

由式(2)可知，等效線性化的基本原則就是在某種準則下合理地選取ce和ke，使所等效的線性方程的解“最優地逼近原非線性方程的解”。

考慮多自由度耗能減震的特點，歐進萍等人提出了采用割線剛度和阻尼系數等概率幅值平均值的等效線性化方法，采用雙線性模型的耗能器的等效線性阻尼和剛度可按下式計算[3，4]:

其中，ce為耗能器的滯變恢復力在位移幅值為a時的等效線性阻尼;ke為耗能器的滯變恢復力在位移幅值為a時的等效割線剛度;ΔW(a)為耗能器的滯變恢復力在位移幅值為a時恢復力曲線包圍的面積;xm為地震作用時耗能器的最大相對位移。

軟鋼阻尼器的恢復力都可近似地用如圖1所示的雙線性模型描述[5]，于是，按式(3)相應的得到耗能器的等效阻尼和等效剛度如下:

其中，kh0為滯變型耗能器與支撐串聯組合單元的初始剛度;xhy為滯變型耗能器與支撐串聯組合單元的屈服位移;α為滯變型耗能器的第二剛度系數;ω為耗能減震結構彈性振動的基本固有頻率。

2 裝有軟鋼阻尼器結構的仿真過程

采用基于割線剛度和阻尼系數等概率幅值平均法對軟鋼阻尼器進行等效線性化，求出軟鋼阻尼器的等效粘滯阻尼系數che和等效剛度khe，則軟鋼阻尼器等效線性化后的控制力可用下式表達:

加入軟鋼阻尼器結構的運動微分方程為:

其中，M0，K0分別為原結構的質量矩陣和剛度矩陣;C0為原結構的阻尼矩陣，采用常用的瑞雷阻尼假定，C0=α1M0+α2K0，α1，α2均為與結構體系有關的常數;{l}為n×1維單位列向量為輸入到結構的地震加速度;Khe，Che分別為軟鋼阻尼等效線性化后的等效剛度和等效粘滯阻尼矩陣，是由式(6)中的khe和che組合形成的矩陣，可表達成下列形式:

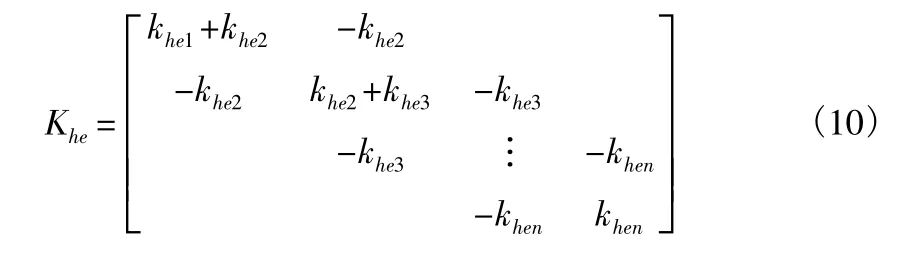
其中，khen，chen分別為第n層阻尼器的剛度總和和阻尼總和。式(7)可用狀態空間描述為:

其中，u=－;0，I分別為n×n維的零矩陣和單位矩陣。

令A=0]，根據該系統的狀態空間描述，可以繪制系統的動態結構框圖，如圖2所示。根據此動態框圖，在Simulink模型編輯器上用相應模塊建立模型[7-9]，在給定的輸入下便可以對安裝軟鋼阻尼器的結構進行動態仿真分析。

3 實例分析

為了便于說明問題，本文以某單跨5層鋼框架為例，對安裝有軟鋼阻尼器的結構在地震作用下進行Simulink動態仿真分析。5層鋼框架結構布置如圖3所示，層高均為800 mm，層間側向剛度kf=250 kN/m，屈服位移uf=15 mm，結構分析中輸入三條地震波，分別為El-Centro波、TAFT波和寧河天津波，峰值加速度均為0.2g。按照GB 50011-2001建筑抗震設計規范對消能減震結構參數范圍的規定[10]，本文選取軟鋼阻尼器的屈服位移ud=2 mm，ud/uf=2/15，SR=8，則耗能減震裝置的剛度kd=2 000 kN/m。軟鋼阻尼器的第二剛度系數α=0.05，極限位移um=30 mm。

在峰值加速度為0.2g的El-Centro波和天津波作用時，分別對安裝有軟鋼阻尼器的有控結構和未安裝阻尼器的無控結構進行Simulink動態仿真分析，畫出結構頂層的位移時程曲線和加速度時程曲線如圖4～圖7所示。

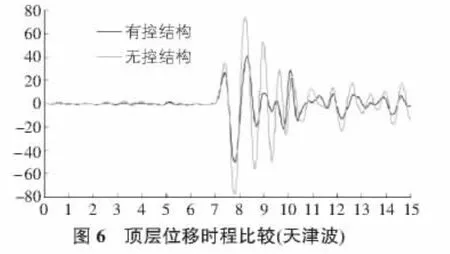
從圖4～圖7中可以直觀地看出，裝有軟鋼阻尼器的有控結構地震反應明顯減小。

4 結語

本文通過對軟鋼阻尼器進行等價線性化處理，引入現代控制理論，運用狀態向量和狀態空間的概念，并借助于MATLAB的Simulink工具箱，對安裝有軟鋼阻尼器的結構進行了動力時程分析。這種分析方法簡潔省時，非常實用。

[1]徐趙東，郭迎春.MATLAB語言在建筑抗震工程中的應用[M].北京:科學出版社，2004:35-44.

[2]Iwan W D，Gates N C.Estimation Earthquake Research of Simple Hysteretic Structures.Journal of Engineering Mechanics Division，ASCE，No.EM3，1979:105.

[3]歐進萍，吳 斌，龍 旭.耗能減震結構的抗震設計方法[J].地震工程與工程振動，1998，18(2):122-124.

[4]歐進萍，王光遠.結構隨機振動[M].北京:高等教育出版社，1998:120-135.

[5]李玉順，大井謙一，沈世釗.極低屈服點軟鋼阻尼器恢復力模型的研究[J].世界地震工程，2004(6):142-145.

[6]張 磊，畢 靖.MATLAB實用教程[M].北京:人民郵電出版社，2008:15-30.

[7]王正林，王勝開.MATLAB/Simulink與控制系統仿真[M].北京:電子工業出版社，2005:218-222.

[8]花炳燦，陳清祥.消能減震技術在某文物保護性建筑加固工程中應用[J].建筑結構，2007(37):19-23.

[9]金來建，宋曉紅，陳清祥，等.中國婦女活動中心二期工程南區酒店結構設計[J].四川建筑科學研究，2007(33):130-133.

[10]GB 50011-2008，建筑抗震設計規范[S].