卡車板簧支架拓撲優化設計

姚芒榮

(陜西重型汽車有限公司，西安710200)

傳統的產品設計是根據經驗設計產品，然后進行反復的物理試驗，驗證設計的合理性，這樣不但費時而且造成不必要的浪費，很不經濟.目前，汽車行業的競爭日益激烈，為了在本行業中設計出既經濟又實用的產品，有限元模擬技術引起了設計人員廣泛的關注。這種技術不僅可以減少反復的物理試驗，避免材料和人工的浪費，而且可以縮短產品設計的周期，促進新產品的早日上市。HyperWorks的OptiStuct模板，是以有限元方法為基礎的最佳優化工具，本文基于此模板，利用拓撲優化技術，建立板簧支架的優化模型，根據優化結果對產品進行了設計，并對設計合理性進行了有限元分析驗證。這種設計思路應該得到大力推廣。

1 拓撲優化

1.1 拓撲優化的數學模型

拓撲優化能夠在給定的設計區域內，尋求結構材料的最合理分布，對于連續結構來說，目前采用的材料流動方法有Homogenization和Density兩種方法。

本論文選用Density法，其基本思想是將連續結構離散為有限元模型，然后引入一種假想的[0，1]之間的密度值，每個單元的密度為設計可變量，這樣就將拓撲優化問題轉化為單元材料密度的最優分布問題，應用最優化準則法或數學規劃方法求解材料最優分布設計，假定密度與材料特性呈非線性關系[1]

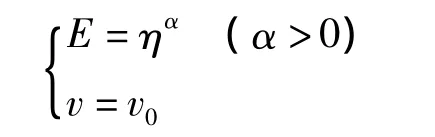
式中:v0——為實際使用材料的特性;

v——為泊松比;

E——為材料的彈性模量。

變密度法數學模型如下:

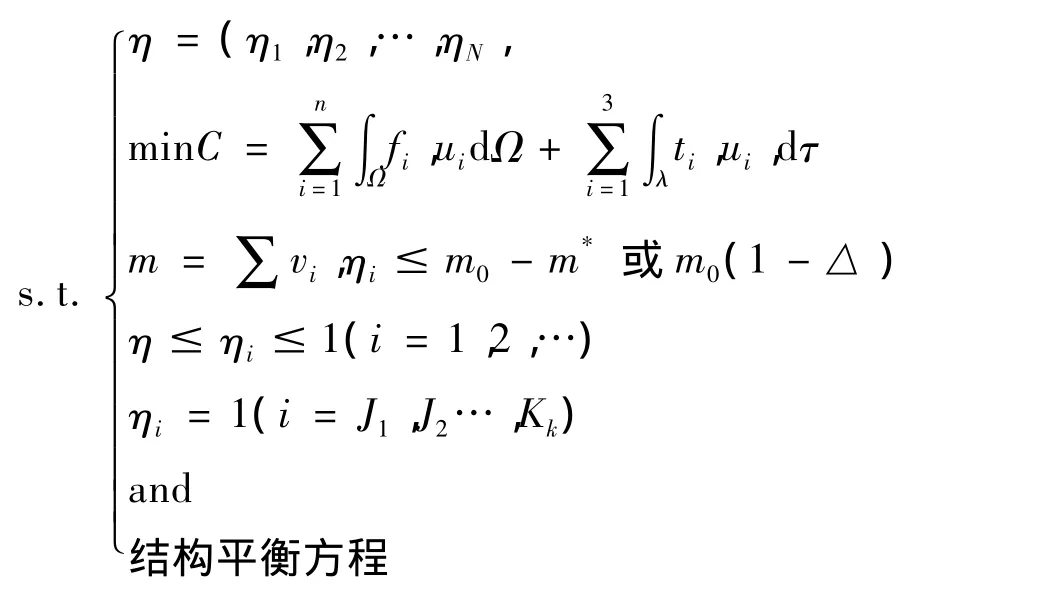
式中:Ω——為設計空間;

τ——為Ω的應力邊界;

ηi—— 為單元密度;

fi——為作用在初始結構上的體積力;

ti——為作用在初始結構上的面積力;

m0——為給定初始結構材料質量的上限;

m*——為優化時指定去除材料的質量;

△——為優化時指定去除質量的百分比;

ηi1—— 為密度下限;J1，J2，…，Jk——為優化后單元密度保持不變的單元號。

1.2 邊界條件

1.2.1 約束邊界條件

根據實際使用情況，如圖1所示和車架連接的5個孔位，除了繞Y軸自由度釋放外，其余5個自由度全部約束。

整個板簧支架受力主要分成兩個部分，第一部分為前板簧對支架的力，第二部分為中間板簧對支架的力。第一部分的力分別為Z向27.5 kN，Y向19.25 kN;第二部分的力分別為Z向27.5 kN，Y向19.25 kN，X 負向19.25 kN.

1.2.2 拓撲邊界條件

圖1為前板簧后支架拓撲模型上定義的設計空間(深灰)和非設計空間(淺灰)。設計空間部分的材料分布將按照Density方法進行拓撲優化。

本拓撲設置位移響應和質量響應，在優化時為了保證整個模型的剛度和強度，根據以往試驗結果，總位移上限定為2 mm，最大應力限制為250 MPa;同時考慮鑄造拔模方式和方向。

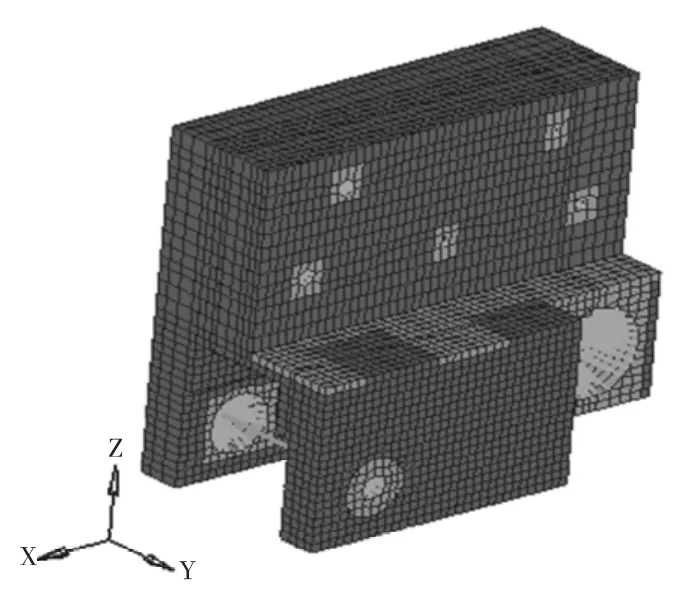
圖1 拓撲空間和非拓撲空間Fig.1 Topological space and non-topological space

1.3 拓撲結果

圖2為61次迭代后最終的拓撲結果，用OSS-mooth導出 igs格式模型，為板簧支架設計提供參考。

1.4 拓撲設計模型

圖3為根據拓撲結果的指導和參照現有的板簧支架，在CATIA中建立的前板簧后支架。

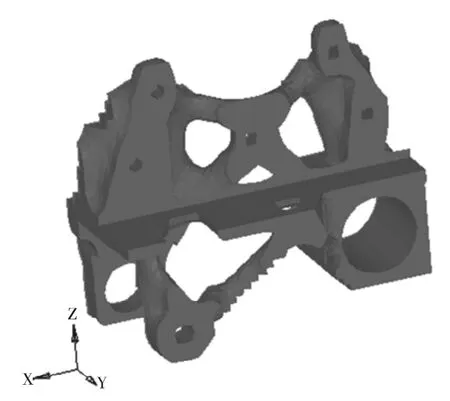
圖2 拓撲結果Fig.2 Topological result

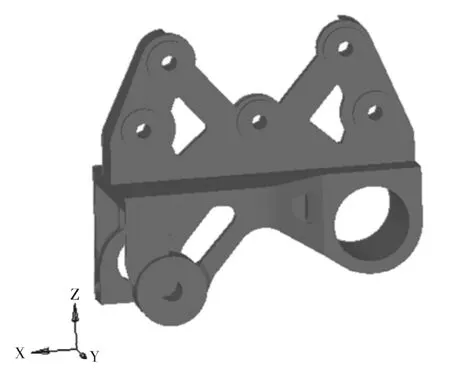
圖3 設計模型Fig.3 Design model

2 驗證設計模型

2.1 設計模型靜強度分析

為了驗證該設計模型的強度，在HyperWorks軟件的OptiStruct模板下，對本支架進行了靜強度分析，結果如圖4所示。通常由于用Rigid單元模型的螺栓連接方式，剛度過大，螺栓孔周圍的應力可以忽略[2]，本結構支架的最大應力為 145.47 MPa。靜強度用屈服極限310 MPa進行校核，安全系數為2.13，靜強度滿足設計和使用要求。

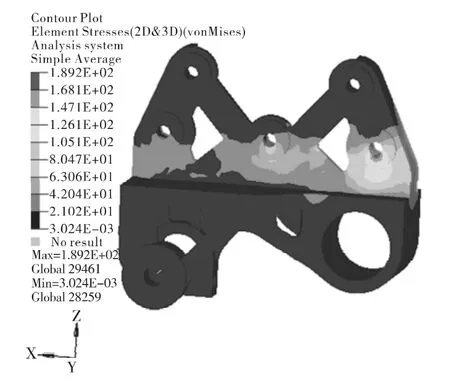
圖4 靜強度分析結果Fig.4 Analysis result of static strength

2.2 設計模型疲勞分析

本論文利用疲勞分析軟件FEMFAT，根據支架實際使用狀態，在靜力計算的基礎上選取正弦交變載荷對本設計支架進行了疲勞強度和壽命分析，結果如圖5和圖6所示。存活率要求99.9%的情況下，安全系數需達到1.32[3]。本結構的最小疲勞安全系數為1.56，最小疲勞壽命為1.0×1011次(設計要求1.0×106次)，滿足設計要求(不考慮螺栓孔周圍的應力)。

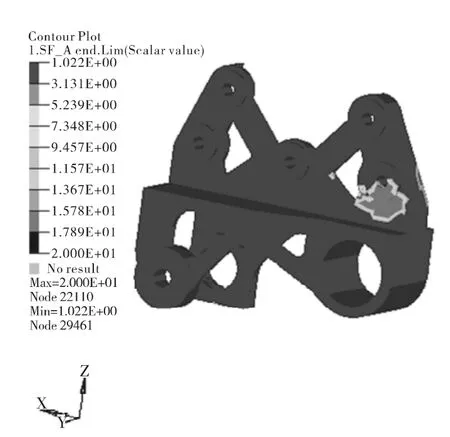
圖5 疲勞強度分析結果Fig.5 Analysis result of fatigue strength

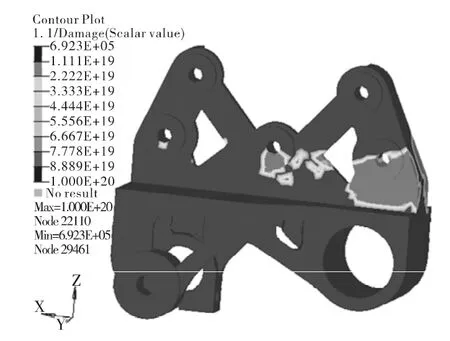
圖6 疲勞壽命分析結果Fig.5 Analysis result of fatigue life

3 結束語

(1)根據拓撲優化結果進行板簧支架設計，能找到模型的最優結構，縮短產品設計周期。

(2)通過有限元模擬技術，對根據拓撲優化結果設計的模型進行強度分析驗證，結果表明新設計的板簧支架，滿足強度要求。

(3)拓撲優化設計是產品的初步優化設計，要完成板簧支架的完整優化設計，還要做進一步的形貌和尺寸優化，對設計進行細化，這種設計思路可以為其它產品結構設計所借鑒。

[1]MLEJNEK H P，SCHIRRMASCHER R.An engineer's approach to optimal material distribution and shape finding[J].Comput Method Appl Mech Eec Engrg，1993，106(1/2):1-26.

[2]張勝蘭，鄭東黎，郝琪，等.基于HyperWorks的結構優化設計技術[M].北京:機械工業出版社，2007.

[3]高鎮同，熊駿江，等.疲勞可靠性[M].北京:北京航空航天大學出版社，2000.

[4]廖焰，劉建生，陳慧琴.新型空心火車車軸重要結構參數有限元分析[J].太原科技大學學報，2007，28(6):446-450.

[5]HAECHANG GEA.Topology optimization，a new micro-structure based design domain method[J].Computers ＆ structures，1996，61(5):781-788.

[6]高英，高昱.重型車前懸架的建立及參數優化[J].太原科技大學學報，2011，32(5):446-450.