鑄態2.25Cr1Mo0.25V鋼的高溫熱變形行為

焦永振，安紅萍，劉建生

(太原科技大學材料科學與工程學院，太原030024)

隨著石油冶煉技術的發展，加氫反應器作為煉油工業中的重要部件向著設備大型化、高性能的趨勢發展。2.25Cr1Mo0.25V鋼以其更高強度、良好的抗高溫回火脆性及優越的抗堆焊層氫剝離性迅速成為了制造加氫反應器的首選材料[1]。目前，國內對該鋼也做了些研究[2-5]，他們研究了鍛態下的組織、性能、工藝熱變形行為。但對鑄態2.25Cr1Mo0.25V鋼的熱變行為涉及相對較少。在熱變形過程中，形變溫度、應變速率和流變應力等熱力學參數都會影響材料的熱變形力學行為，而材料的熱變形力學行為，又是衡量材料塑性加工性能的一個重要指標。本工作研究了2.25Cr1Mo0.25V鋼在鑄態下的熱變形行為，分析在熱壓縮過程中熱力學參數之間的關系，為相關的數值模擬提供數據基礎。

1 試驗方法與過程

本次試驗所用材料為中國二重冶煉的234t大型2.25Cr1Mo0.25V鑄態鋼錠，取樣位置位于錠身處距冒口1 400 mm處，從鋼錠中心部位，沿半徑方向由內而外的等軸晶區內，其化學成分如下表所示:

表1 2.25Cr1Mo0.25V鋼的化學成分(%，質量分數)Tab.1.Chemical compositions of 2.25Cr1Mo0.25V steel in wt%

將取下的材料制成尺寸為?8×12 mm的圓柱體試樣，采用Gleeble-1 500D熱模擬試驗機做熱壓縮試驗，形變溫度分別為950℃，1 050℃，1 150℃，1 250 ℃，應變速率分別為 0.005 S-1，0.01 S-1，0.1 S-1，真應變為 0.5，試驗流程如圖所示(圖 1)。

試樣高溫變形后，應立即進行急冷，使其保留高溫形變結束時的組織。將熱壓縮變形后的試樣，采用線切割機床沿軸線方向剖開后，進行磨制、拋光，用加洗潔精的過飽和苦味酸溶液在40℃的溫度下進行腐蝕，并采用ZAISS Imager.A1m光學顯微鏡觀察組織，用截線法測量觀察到的晶粒尺寸，測定晶粒個數不少于300個。

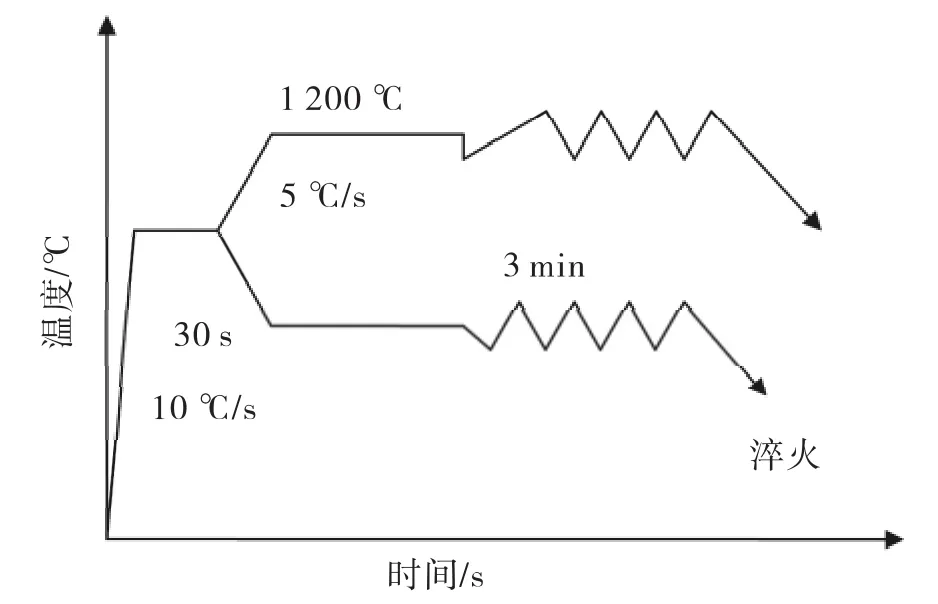
圖1 實驗流程圖Fig.1 The experiment procedure

2 試驗結果與分析

2.1 不同形變參數下的真應力-應變曲線圖

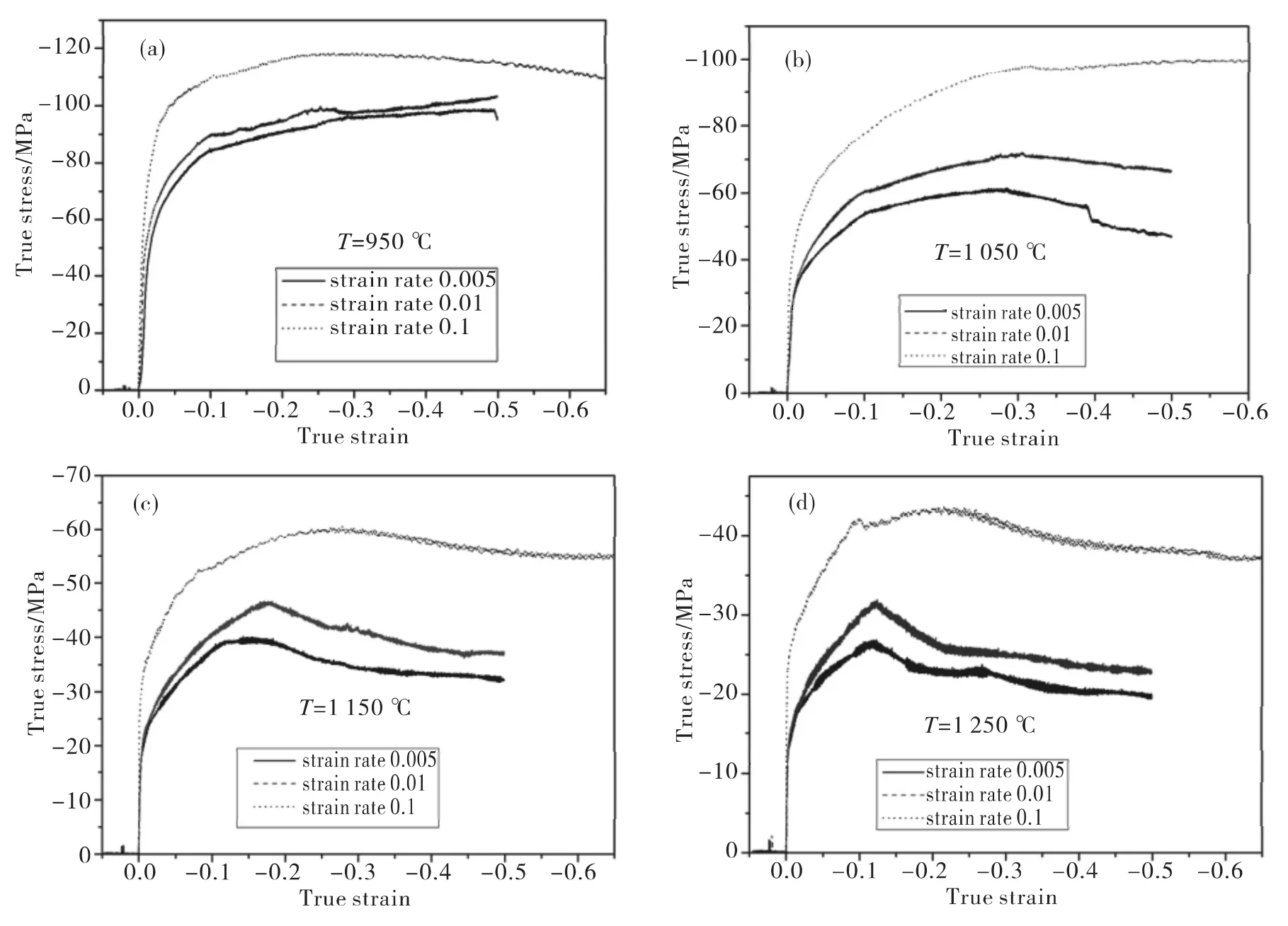
圖2 不同變形條件下的真應力-真應變曲線Fig.2 True stress-true strain curves under different deformation conditions

圖2是最大變形量為40%時，在不同的溫度和應變速率下的真應力-應變圖。從圖中可以看出，應力應變曲線的類型包括，加工硬化型曲線、動態回復型曲線和動態再結晶曲線。在溫度較低，應變速率較大的條件下，真應力應變曲線呈動態回復型;在溫度較高，應變速率較低的條件下，真應力應變曲線呈現動態再結晶型。

溫度為950℃，應變速率為0.005 S-1和0.01 S-1條件下的應力應變曲線的特征為，流變應力隨著應變值的增加而增大，符合屬于加工硬化型應力應變曲線的變化規律。溫度為950℃，應變速率為0.1 S-1和1 050℃各個應變速率條件下的曲線特征為，其流變應力隨應變的增大而增大，當達到某個定值時逐漸趨于穩定狀態，符合動態回復型曲線的變化規律。在溫度為1 150℃和1 250℃的條件下，各應變速率下的曲線的特征為，流變應力先增大到一個峰值，然后隨應變的增加，流變應力有所降低，降低到某一定值后進入一個穩態的平衡階段，該特征符合動態再結晶類型曲線的變化規律。

從應力-應變曲線圖2中可以看出，在溫度和應變量相同的條件下，應變速率越低，峰值應力越小，峰值應變越小。如在溫度為1 050℃，應變速率為0.1S-1條件下的峰值應力為 100.12 MPa，應變速率為 0.01 S-1條件下的峰值應力為 72.028 MPa，應變速率為0.005 S-1條件下的峰值應力為61.357 MPa.由于應變速率較低時，動態再結晶容易發生，抵消了加工硬化作用，使得材料的流變應力降低。隨著應變速率的提高，峰值應力和應變會隨之增大，動態再結晶會變得困難。由于應變速率的增加，峰值應力增大，導致變形抗力增大，不利于動態再結晶的進行，因此在該條件下加工硬化在熱壓縮過程中占主導地位，致使流變應力增大。

在應變速率和應變量相同的條件下，材料的流變應力、峰值應力和峰值應變均隨著形變溫度的升高而呈現降低的勢態。如在應變速率為0.005 S-1，溫度為950℃的條件下，峰值應力為98.892 MPa，溫度為1 050℃的條件下，峰值應力為61.357 MPa，溫度為1 150℃的條件下，峰值應力為40.023 MPa，溫度為1 250℃的條件下，峰值應力為26.815 MPa。由于當形變溫度較低時，能量較低，無法使位錯產生攀移和交滑移，此時加工硬化率大于動態再結晶和回復的軟化速率，該階段主要發生加工硬化。隨著溫度升高，原子運動能力增強，空位密度增大，位錯運動的驅動力增大，動態再結晶會很容易發生。動態再結晶會完全或部分消除了加工硬化效果，使流變應力逐漸降低。曲線的峰值應變也隨溫度的升高而減小，較流變應力與峰值應力而言相對緩慢，受溫度影響較弱。

2.2 高溫熱變形本構方程和形變激活能的確定

熱變形激活能是發生動態回復和動態再結晶的動力，其大小決定了變形過程中的動態回復和動態再結晶發生的情況。Arrhenius方程包含了變形激活能Q、溫度T和應變速率˙ε之間的關系[3-6]。

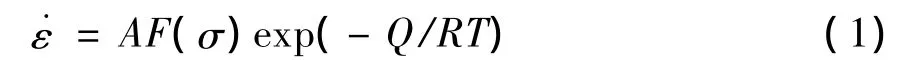
其中，F(σ)有三種形式，當應力較低時，即:ασ ＜ 0.8時，F(σ)= σn1;

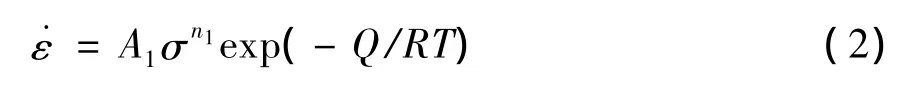
當應力較高時，即ασ ＞ 1.2時，F(σ)=exp(βσ)

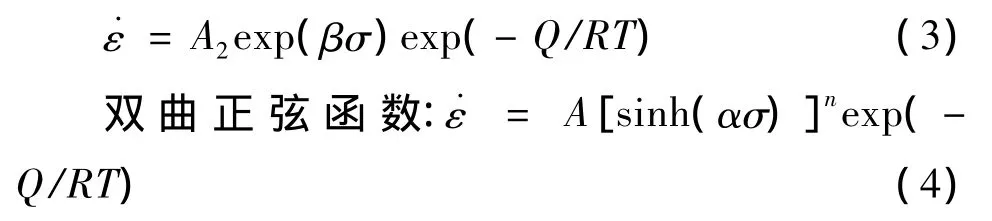
雙曲正弦函數適用于不同溫度、應變率和應變下的應力;式中:˙ε為應變速率(s-1);R為氣體常數(8.31 J/mol·K);T為絕對溫度(K);Q為形變激活能(kJ/mol);σ 取峰值應力 σp(MPa);A，A1，A2，α，n和n1為材料常數，其中α=β/n1.

對式(1)和(2)，兩邊求對數得:

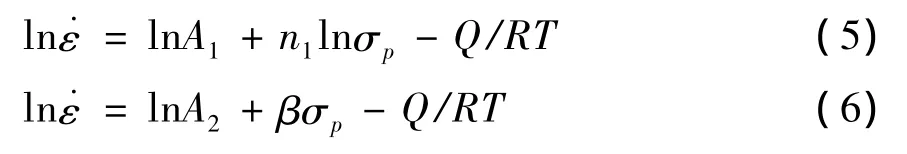
當形變溫度相同時，上式中的lnA1、lnA2和Q/RT均為常數。分別繪制lnσp、σp和ln˙ε的關系圖(圖3、圖4)。線性回歸得出不同溫度下的斜率，對其倒數求平均值得出n1=9.267 32;采用相同方法可求出 β =0.141 19，則 α = β/n1=0.015 2.

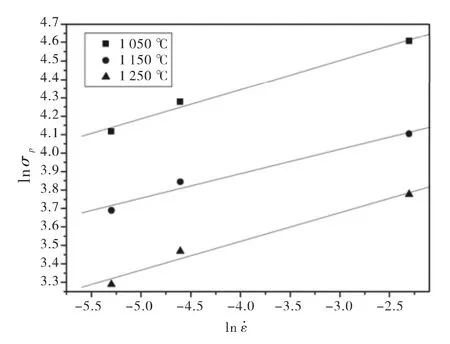
圖3 lnσp與ln˙ε的關系Fig.3 Relationship between lnσpand ln˙ε

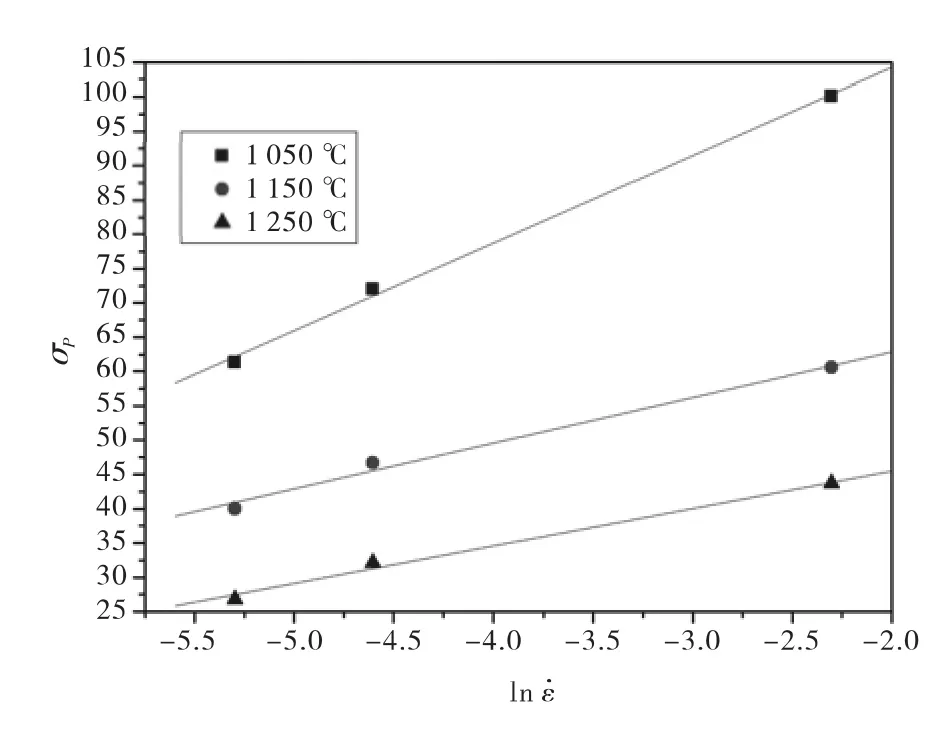
圖4 σp與ln的關系Fig.4 Relationship betweenσpand ln

對(4)式，兩邊取對數得:

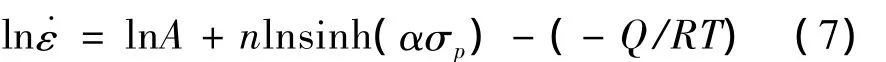
并對式(7)進行偏微分，得出形變激活能的Q的表達式:

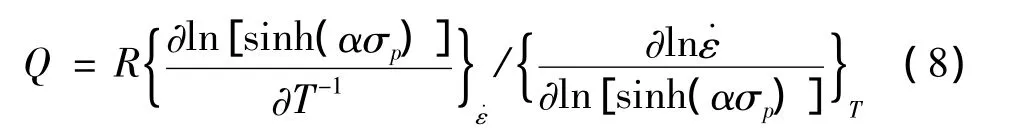
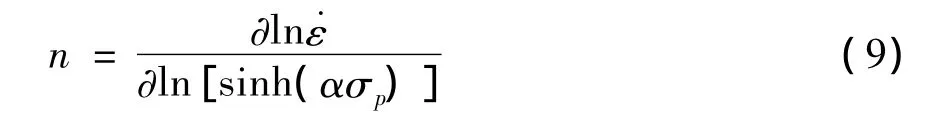
當溫度不變時，n的求解關系式可表示為:

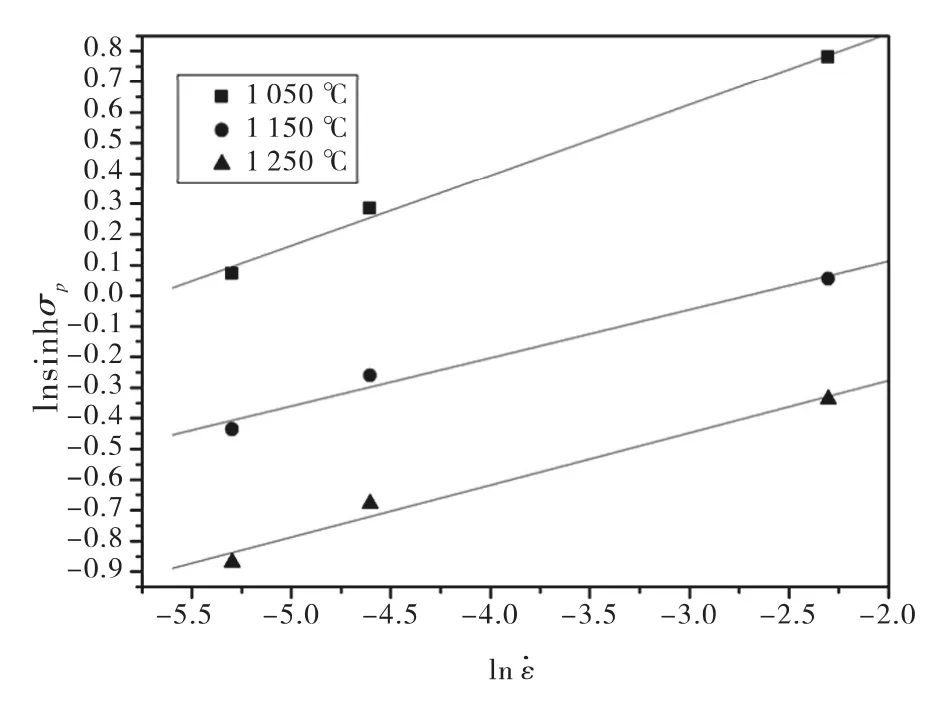
圖5 ln[sinh(ασp)]與ln的關系Fig.5 Relationship between ln[sinh(ασp)]and ln

當應變速率不變時，形變激活能的關系式可表示為:

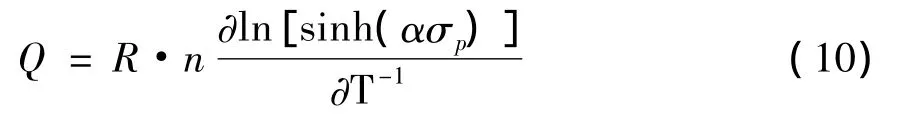
對ln[sinh(ασp)]和10 000/T的關系作圖6，可得出平均值為0.61，將上述擬合出的數值帶入Q的表達式:Q=R·n × 0.61=305.312 kJ/mol.

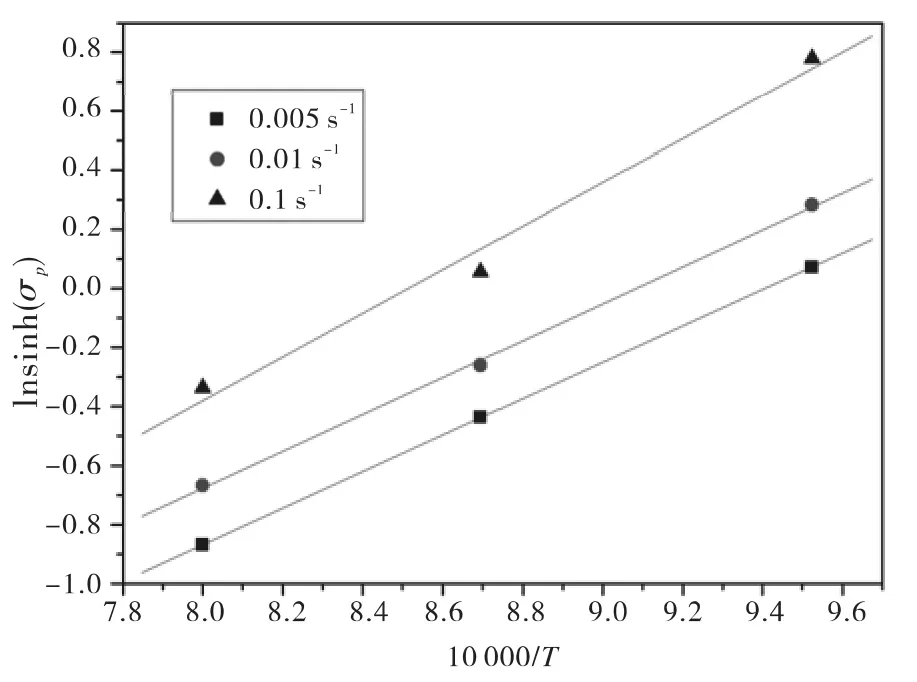
圖6 ln[sinh(ασp)]與溫度T的關系Fig.6.Relationship between ln[sinh(ασp)]and temperature

高溫塑性本構關系體現了流變應力、形變溫度和應變速率等變形過程中熱力學參數之間的關系。Zener和Hollomon在1944年研究鋼的應力-應變關系時發現，他們取決于應變速率和形變溫度T，其關系可以用Zener-Hollomon參數來表示[7]:

式中Z是Zener-Hollomon參數，是用溫度補償了應變速率，Q為形變激活能，引入雙曲正弦函數可得:

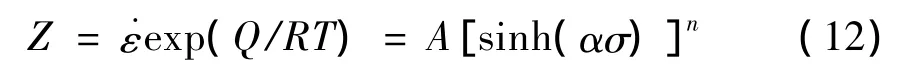
將求得的Q值、溫度、應變速率及其它參數帶入式(11)中，在得到lnZ值后，對式(12)兩端求對數，并對 lnZ-ln[sinh(ασp)]作關系圖7.

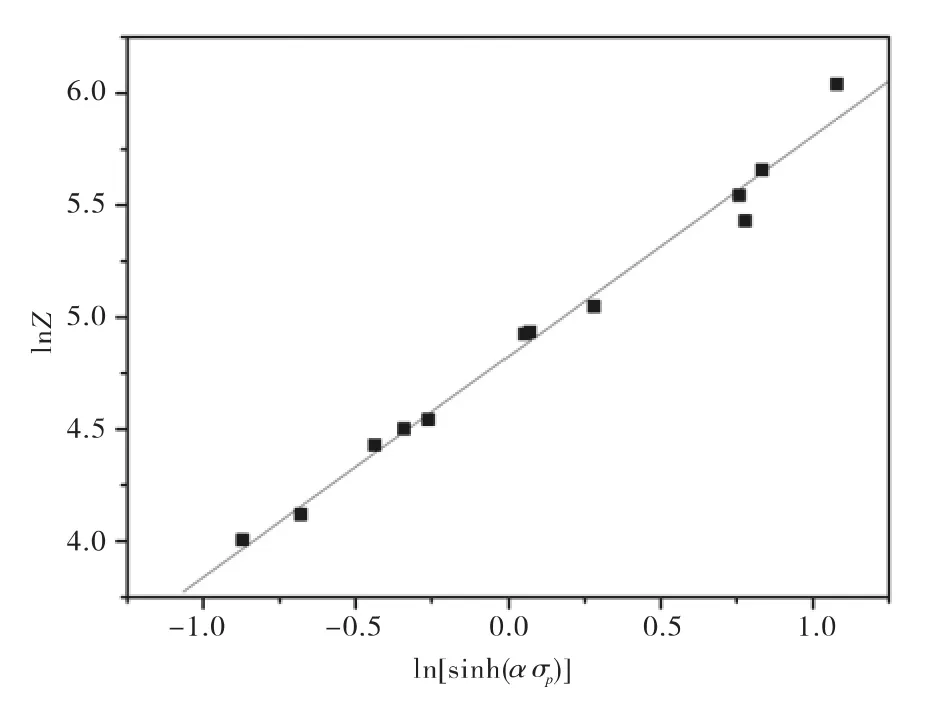
圖7 lnZ 與 ln[sinh(ασp)]關系圖Fig.7 Relationship between ln[sinh(ασp)]and lnZ

由圖7可以看出lnZ與ln[sinh(ασp)]呈線性關系，其線性相關度達到99.3%，由此表明可以用雙曲正弦函數來描述高溫熱變形過程的本構關系。而lnA為線性回歸的截距，則lnA=29.053 3，則A=4.15×1012S-1;將擬合出的各個數據帶入雙曲正弦函數，可得到本構方程:

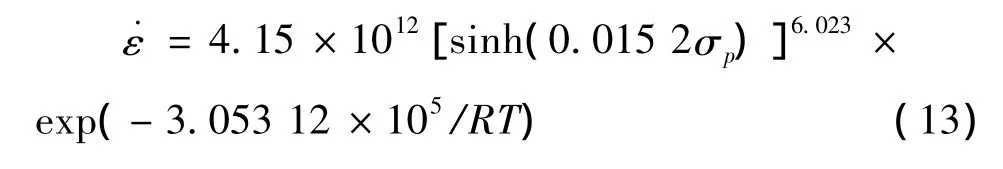
則Z參數可表示為:

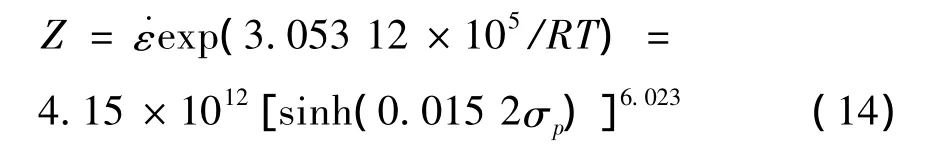
3 結論

(1)通過對鑄態鋼2.25Cr1Mo0.25V高溫形變過程中應力-應變曲線的研究得出，隨著形變溫度的升高和應變速率的減小，流變應力減小，峰值應力和應變降低，但應變速率為0.005 S-1和0.01 S-1時，4個溫度下的流變應力值較為接近。

(2)確定高溫變形過程中的形變激活能Q為305.312 kJ/mol，并建立該過程中的本構方程為:

˙ε=4.15×1012[sinh(0.015 2σp)]6.023×exp(-3.053 12 × 105/RT)

[1]陳曉玲，李多民，段滋華.加氫反應器的發展現狀[J].化工裝備技術，2009，30(1):29-30.

[2]張景利，付瑞東，王純宇，等.2.25Cr-1Mo-0.25V 鋼的熱變形行為及其形變組織[J].塑性工程學報，2010，17(3):45-49.

[3]RAO K P，H AW BOLT E.Development of constitutive relationships using compression testing of a medium carbon steel[J].Transactions of the ASME Journal of Engineering Materials and Technology，1992，114(1):116-123.

[4]HEE Y.KIM ，SOON H Hong.High temperature deformation behavior and microstructral evolntion of Ti-47Al-2Cr-4Nb intermetallic alloys[J].Scripta Materialia，1998，38(10):1517-1523.

[5]GRONOSTAJSKI Z J.Development of constitutive equation of copper-silicon alloys[J].Journal of Materials Processing Technology，1996，60(5):621-627.

[6]柏永清，陳明明，陳慧琴.316LN熱變形行為及動態再結晶晶粒的演變規律[J].太原科技大學學報，2009，30(5):424-425.

[7]ZENER C，HOLLOMON J H.Effect of strain-rate up on the plastic flow of steel[J].J Appl Phys，1944，15(1):22-32.