乒乓球戰術行為博弈分析的理論體系建構

劉文明，唐建軍

（1.浙江大學 教育學院體育學系，浙江 杭州310028；2.北京體育大學，北京100084）

乒乓球運動競賽必然存在某種意識程度上的“交叉效應”，即一方運動員的行為勢必會影響對手的策略選擇與比賽結果，這種雙方隊員對交叉效應的認識，以及雙方據此認識而采取的戰術行動，構成了乒乓球運動競賽取勝的核心。若三思而后行——明白對手的目標和偏好，以及行動的約束和限制，并根據自己的標準以一種謀略方式選擇行動以期得到最好結果——則可稱為在理性地行動［1］博弈論為乒乓球戰術行為分析增加了一個維度，即與其他決策者的互動。博弈論是關于互動情形下理性行為的科學，不能說博弈論對乒乓球戰術進行分析就可以教給我們對抗的秘訣，或確保永不失敗［2］因為絕大多數現實乒乓球比賽情形包含了大量的特異性反應和機會元素，但是博弈論可以提供一些思考策略互動問題的一般性原理，可以告訴我們在謀劃一個成功策略之前，必須把這些博弈思想和一些具體的計算方法補充到現在所處的場合中，這時博弈論的一般性原理能夠為運動員、教練員提供了一個參照點，可以更快、更自信地歸納和總結出具體乒乓球戰術博弈特征，在行動中增大成功概率。

1 乒乓球戰術行為博弈理論的概念

“博弈”是社會生活中存在的形形色色的需要依靠策略戰勝對手的，具有競爭性和對抗性的現象。博弈競爭就是社會實踐中有規則可循的、采用計謀的、富有理性的、期望得到理想或滿意結果的競爭。體育博弈，是在一定的競爭規則的限定下進行，最具理想意義的競爭。隨著體育運動實踐的發展，其中充滿了各種沖突、對抗與競爭表現出鮮明的博弈特征，促進了體育博弈理論的形成。“體育博弈論”是關于體育競爭的理論體系，是研究體育競爭中如何戰勝對手，提高勝算，獲取優勝的理論（李益群、謝亞龍）［3］。首先，乒乓球運動實踐是一種體育博弈現象，具有強烈的競爭性、對抗性和戰術行為策略性；其次，乒乓球戰術行為策略具有顯著的互動性、相互依存性的特點，即戰術行為的交叉效應；再者，乒乓球戰術行為的最終目的就是戰勝對手取得比賽的優勝。由此三個方面確定了乒乓球戰術行為博弈理論，即是關于乒乓球戰術行為合理運用的理論體系，是研究如何在乒乓球競賽實踐中戰勝對手，提高勝算，獲取比賽優勝的理論。乒乓球戰術行為博弈理論是以“博弈論”的基礎理論、思想方法去研究和探索乒乓球技戰術在競賽過程中合理運用的微觀問題的理論，探討在乒乓球運動競賽中如何去戰勝對手、提高勝算、獲取優勝的科學理論。

根據乒乓球比賽規則和戰術行為的交叉效應，乒乓球競賽戰術實施過程可以表示為相互作用的耦合系統，根據戰術實施過程的相互制約關系，把對抗中參與人所擁有的戰術行為集合為，所實施的戰術行動表示為 （戰術策略選擇及實施如:發球落點）看作是對參與人所發生的作用效應，而參與人所擁有的戰術行為集合表示為，對的戰術行為的反應行可表示為（戰術策略選擇及實施如:接發球落點）是參與人對參與人的作用所產生的反作用，并再次作用于參與人，如此反復進行。這樣博弈雙方之間形成耦合系統關系，如圖1所示。

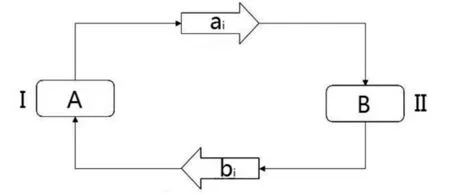
圖1 乒乓球競賽戰術行為實施過程耦合關系模型

2 乒乓球戰術行為博弈的構成要素

2.1 乒乓球戰術行為博弈參與人（players）

乒乓球戰術行為的博弈人是指在乒乓球戰術行為博弈中獨立決策、獨立承擔博弈結果的個人或者組織，每個參與人的目標都是通過選擇行動來最大化自身的效用。只要在一個博弈中統一決策、統一行動、統一承擔結果，不管一個組織有多大，哪怕是一個國家，甚至是多個國家組成的聯合國，都可以作為博弈中的一個參與人。正在比賽狀態時，乒乓球戰術行為的發起者為參與競爭的乒乓球運動員，因此乒乓球戰術行為的博弈人為直接參與實施技戰術的乒乓球運動競賽的運動員。但教練員往往是運動員戰術行為或者是策略的制定者，同時在比賽中也可以實施暫停、手勢等等手段間接性參與到乒乓球戰術行為的實施過程中，并往往對比賽結果產生巨大影響，所以也是乒乓球戰術行為博弈中的重要參與人之一；其次，科研人員對技戰術的研究也在逐步地深入到運動實踐，給運動員、教練員提過決策支持等，也對乒乓球競賽戰術的使用產生一定的影響。

2.2 乒乓球戰術行為博弈的行動（actions or moves）

乒乓球戰術博弈中的行動，是參與人在博弈的某個時點的決策變量，在乒乓球運動實踐中行動可以指在競賽過程中某階段如發球、接發球、第三拍、第四拍和相持過程中的技戰術運用，理論上可以從三個層次進行劃分:①戰術層面有“發球搶攻”，“接發球搶攻”等；②技術層面有控制技術（擺短、劈長）、防守技術（推擋、放高球）及進攻技術（挑打、拉攻）等；③制勝因素層面有力量、旋轉、線路、落點、弧線等。

60年代初為中國乒乓球隊備戰第26屆世乒賽形成技戰術診斷指標開始，直至第47屆世乒賽科研攻關與科技服務的40多年中，確定科研與實踐都相對固定的診斷指標。指標體系確定是從實踐需要開始，并經過實踐篩選，再到實踐檢驗的過程［4］第24、25、26、27屆奧運會和其間的4屆亞運會及7屆世界錦標賽備戰訓練的檢驗，證明是可靠的。其中四和五級指標的劃分可以看作戰術行動在不同博弈分析角度的具體體現，見表1。

表1 戰術診斷比賽效果的四級和五級指標

2.3 乒乓球戰術行為博弈的信息（information）

在乒乓球戰術行為博弈中信息是參與競爭的雙方運動員有關此場比賽的博弈知識，有關對手特征和行動的知識。也可以具體表述為雙方運動員在特定時間點對于自己和對手特定行動功效的了解。如賽前的比賽技戰術分析（錄像觀察、經驗總結）、比賽中已經發生的具體行動知識和對彼此戰術風格的了解等都是乒乓球戰術博弈的信息。“知己知彼，百戰不殆”體現了博弈信息的重要性，現代比賽技戰術分析工作已經非常深入，對運動員的技戰術分析也相當全面，中國乒乓球隊建立了大量的國外乒乓球運動員的戰術信息庫。并能夠以多媒體的形式來展現國外主力隊員的技戰術信息。

基于比賽視頻技術發展起來的多媒體技戰術分析，能以視頻、動畫和圖表數據等多種形式清楚有序，生動形象地將對手的技戰術特點展示出來，從而有效地幫助教練員和運動員更加細致地觀察、分析對手，提高大賽前備戰訓練的針對性與科學性［5］。

圖2 中國國家乒乓球隊業務學習多媒體資料

乒乓球戰術博弈信息的特點是參與競爭雙方的運動員的“共同知識”（common knowledge），這是一個非常重要的概念［6］。共同知識指的是“雙方乒乓球運動員知道，雙方運動員知道雙方運動員知道，雙方運動員知道雙方運動員知道雙方運動員知道…的知識”，在乒乓球戰術博弈中，每個參與人的行動集合都是共同知識。比如說參與人知道自己的行動集合，參與人知道參與人的行動集合，參與人知道參與人知道自己的行動集合，參與人知道參與人知道參與人知道自己的行動集合，如此等等。

2.4 乒乓球戰術行為博弈的戰略（strategies）

乒乓球戰術行為博弈的戰略指的是參與人（乒乓球運動員）在給定信息的情況下的行動規則，它規定了參與人（乒乓球運動員）在什么時候選擇什么行動。因為信息集包含了一個參與人有關其他參與人之前行動的知識，戰略告訴該參與人如何對其他參與人的行動做出反應，因而戰略是參與人（雙方運動員）的“相機行動方案”（contingent action plan）。

乒乓球戰術行為博弈的戰略根據乒乓球項目具體實施過程可進行兩個層面的劃分:乒乓球戰略構成策略層面可以理解為戰術單元、單個戰術和若干單個戰術構成的戰術體系——戰術風格。乒乓球戰術最基本的戰術形式是戰術單元，所謂戰術單元是指單一技術的戰術化，比如目的性、策略性地使用發球而直接得分。而所謂策略，是指在單一技術的使用中，根據對手情況，通過速度、力量、旋轉和落點線路的變化來爭取得分。戰術單元是構成戰術的基本“細胞”，兩個以上的戰術單元構成了單個戰術。所謂單個戰術就是結合技術的戰術化，如反手用推擋壓住對手反手大角度獲得主動后，伺機側身正手進攻得分。若干單個戰術組合構成一個戰術體系［7］

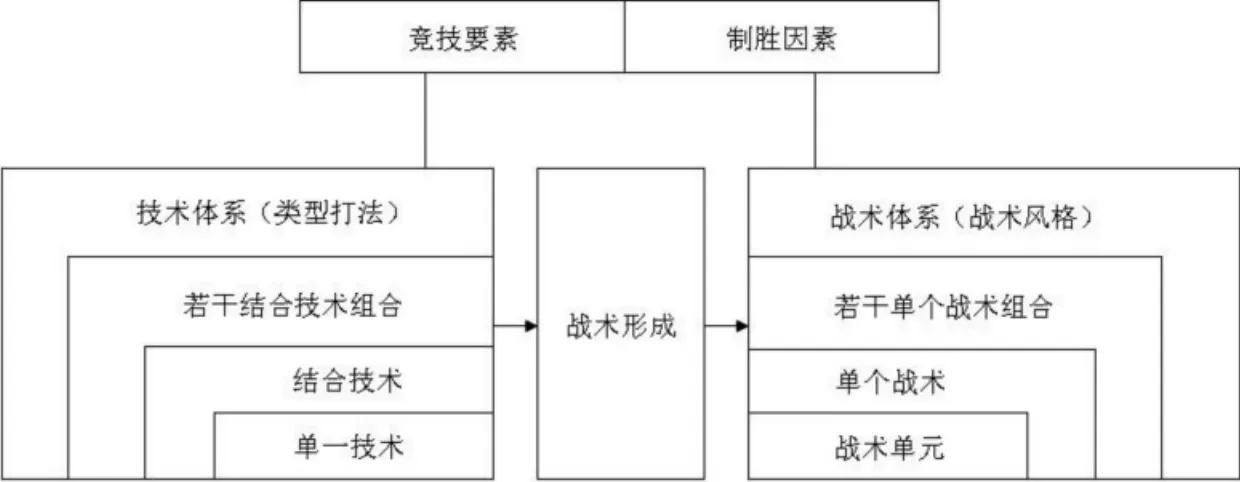
圖3 乒乓球技術、戰術和戰術形成結構與關系模式圖

乒乓球戰術行為博弈的戰術層面主要指戰術的數量，包括進攻戰術的數量、控制戰術的數量和防守戰術的數量。戰術數量是戰術能力在數量上的體現，它是戰術質量存在的基礎。在比賽中單一戰術，會使對手很快適應，在高水平的比賽中是沒有質量可言的。在乒乓球的基本戰術中進攻打法類型的戰術包括:發球搶攻戰術；對攻戰術；拉攻戰術；搓功戰術；接發球戰術。削攻或削攻結合打法類型的戰術包括:發球搶攻戰術；削攻（攻削）結合戰術；搓、攻、削結合戰術；搓攻戰術；接發球戰術。運動員必須掌握多種戰術，才能提高戰術的應變能力，爭取戰術運用的主動［7］。

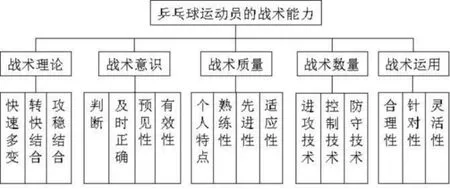
圖4 乒乓球運動員戰術能力系統構成圖

2.5 乒乓球戰術行為博弈的得益（payoffs）

支付在乒乓球戰術行為博弈中指的是特定戰略組合下參與人（雙方運動員）的確定效用水平，或是指參與人得到的期望效用水平。對應于乒乓球戰術行為博弈方的每一組可能的決策，都有一個結果表示該策略組合下各博弈方的所得或所失。支付是乒乓球戰術行為博弈的參與人真正關心的東西。在此處應該強調的是由于乒乓球比賽計分規則的特殊性，所以博弈雙方的得益可進行個多層次的劃分，即一分球的得失；一局球的勝負；一場比賽的輸贏。得益即參加乒乓球戰術行為博弈的各方從博弈中所獲得的利益，它是各博弈方所追求的根本目標，也是戰術行為和判斷的主要依據。乒乓球戰術博弈必須對得益做出規定，得益可以是正值，也可是負值，得益是分析博弈模型的標準和基礎。在乒乓球戰術行為的博弈過程中，最直接的目的贏得每一分，博弈的直接結果是一分球的得失，進而變成一局球的得失，最終通過局數的得失決定整場比賽的勝負。所以，乒乓球戰術行為的直接得益（一分球的得失）與戰術行為的最終得益（一場比賽的勝利）存在間接性的相關關系。這里的根本目標不是前兩個層次而是在第三個層次（一場比賽的勝利），因為在乒乓球項目中存在得分多并不能贏得比賽的現象［8］。

2.6 乒乓球戰術行為博弈的次序（orders）

在乒乓球戰術行為博弈過程中參與人即雙方運動員在進行獨立決策時，也就是戰術行動的實施過程是有順序、先后進行，并且不止一次地進行決策選擇，乒乓球戰術博弈中行動順序對博弈結果有著非常重要的影響。在規定一個博弈時必須規定其中的次序，因為即使博弈的其他方面都是相同，次序不同一般就是不同的博弈類型，同樣的參與人，同樣的行動集合，行動的順序不同每個參與人的最優選擇就不同，博弈的結果就不同（事實上，不同的博弈順序意味著不同的博弈）。特別是在不完全信息博弈中，后行動者可以通過觀察先行動者的行動來獲得信息，從而使得博弈分析成為預測人的行為的一個有力工具，在乒乓球戰術行為博弈當中，如發球段的技戰術行為實施和接發球段的技戰術行為實施存在明顯的差別，對博弈結果也有重要的影響。乒乓球戰術行為博弈的行動是劃分乒乓球戰術行為博弈類型的一個重要標準（靜態博弈和動態博弈）。在乒乓球戰術行為博弈論中一般假定參與人的行動空間和行動順序是所有參與人的“共同知識［9］”。

2.7 乒乓球戰術行為博弈的結果（outcome）

乒乓球戰術行為博弈結果是博弈分析者所感興趣的所有東西，如乒乓球戰術博弈的均衡戰略組合，均衡行動組合，均衡支付組合等，從實踐的角度上講是對比賽雙方運動員乒乓球戰術行為運用規律的認識，有助于提高運動員的比賽獲勝概率；從理論的角度講是對乒乓球項目本質規律的深入認識，對乒乓球項目發展有著巨大的促進作用。

2.8 乒乓球戰術行為博弈的均衡（equilibrium）

均衡是乒乓球戰術行為博弈參與人雙方的各自最優戰略組成的一個戰略組合。乒乓球戰術行為博弈中的均衡概念包括優勢策略均衡（Dominant Strategy Equilibrium）、混合策略均衡（Mixed Strategy Nash Equilibrium）、納什均衡（Nash Equilibrium）［10］。

3 乒乓球戰術行為的博弈類屬研究

3.1 博弈人數

根據博弈的參與人數的多少可以分為二人博弈和多人博弈。乒乓球比賽都是雙方爭勝的比賽，直接表現為雙方為一場比賽勝負進行戰術行為的互相制約和反制約，如果是雙打比賽也可把場上的同隊兩個隊友看作一個博弈方，所以乒乓球戰術行為博弈為兩人博弈。

3.2 博弈次序

根據博弈行動的次序可將博弈分為序貫行動（sequential moves）和同時行動（simultaneous moves）兩種博弈類型。乒乓球戰術行為在實施時嚴格遵守時間序列，即一拍擊球后（發球）接著是對手的一拍擊球（接發球），接著到發球搶攻或控制（第三拍）和接發球搶攻或控制（第四拍），再到相持階段。每個乒乓球運動員都必須思考:如果我這樣做，我的對手會怎樣反應？對未來結果的計算支配著乒乓球運動員當前的行動。從乒乓球戰術行動的實施過程角度，乒乓球戰術行為博弈應屬于序貫博弈。

3.3 得益特點

根據博弈得益的特點如一方贏就是另一方輸，得失總和為零，這類博弈可稱為零和博弈（zero－sum games），更一般的講，零和博弈的思想就是參與人利益完全沖突的；如果利益并不是精確為零，可稱為常和博弈（constant－sum games）。乒乓球競賽雙方的利益完全沖突，一勝一負相伴而生。乒乓球競賽中一方的得分必是對方的失分，在一分球的博弈中雙方戰術得益（得失分）的總和為零，在一局球、一場球的總得益（總得失分）的總和也是零。即參與競爭雙方的利益完全沖突，因此乒乓球戰術行為從得益（得失分）角度上應屬于零和博弈。

3.4 博弈次數

在乒乓球競賽中，并不是簡短單一的一分球的爭奪，而是以一分球為得益單位的多次戰術行為的互動博弈，每一分球的爭奪都是從發球、接發球、第三拍、第四拍……直至一分球結束，再到一局的輸贏，最后才能最終決定比賽的勝負。在這里得分多并不一定能夠取得比賽勝利，也是乒乓球博弈的一個特點。所以乒乓球戰術行為博弈屬于重復博弈，這樣在持續多次的重復博弈過程中，給我們提供了分析博弈雙方的戰術行為“路徑依賴”和博弈“納什均衡”的可能性。

3.5 博弈信息

在臨場乒乓球戰術行為博弈的實施過程中，雙方都了解目前的戰況以及過去的過程，并且也都知道對手以贏得比賽為目標。但在此類博弈過程中，博弈雙方在每個行動點上是無法獲悉決策所需的全部信息的，如對手將把球回到什么位置以及怎么配套等，所以可以稱這種情況為不完美信息（imperfect information）。在賽前比賽技戰術行為分析時，當乒乓球博弈參與人一方比另一方了解更多信息時，這類情況稱為不完全信息（incomplete information）或者非對稱信息（asymmetric information）就會相應產生詭計和陰謀［11］此時乒乓球戰術博弈參與人可以推測、隱藏或傳遞錯誤信息，這都是乒乓球戰術博弈策略的重要組成部分。在博弈過程中參與人所擁有的信息對博弈的結果有重要的影響，當參與人擁有不同的信息時，如何操縱和信息本身就是一場博弈，甚至比后續的博弈更為重要。

3.6 博弈規則

乒乓球戰術行為博弈的規則是確定的，是所有參與人必須遵守的。比賽規則包括乒乓球比賽的物質條件如球臺、球網裝置、球、球拍，比賽條件如場地要求等；比賽中的基本概念；比賽的勝負機制；比賽紀律等。乒乓球比賽規則保證了乒乓球戰術行為博弈的公平競爭，機會均等原則。國際奧委會要盡可能地平均分布奧運會金牌的精神，國際乒聯對乒乓球的競賽規則作了一系列的重大改變:2000年10月將乒乓球比賽中一直使用的直徑為38mm的乒乓球改為直徑為40mm的大球，2001年9月1日將原來乒乓球的21分賽制改為11分賽制，從2002年9月1日起實行新的發球規定，也叫無遮擋發球。2008年9月，國際乒聯的禁膠令頒發，奧運會后，這一禁令全面執行，乒乓球進入“無機膠水”時代。乒乓球博弈規則的每一次修改都對乒乓球技戰術的使用有著非常明顯的影響。

4 乒乓球戰術行為博弈的表述方法

一個博弈可以用兩種不同的方式來表述，一種是戰略式表述（strategic form representation），另一種是擴展式表述（或者譯為“展開式表述”）（extensive form representation）。盡管理論上這兩種表述形式幾乎是完全等價的，但從分析的方便性的角度來講，戰略式表述更適用于靜態博弈，而擴展式表述更適合于討論動態博弈［12］

4.1 乒乓球戰術行為博弈的戰略式表述

戰略式表述又稱標準式表述（normal form representation），在這種表示中，所有參與人同時選擇各自的戰略，所有參與人選擇的戰略一起決定每個參與人的支付。請注意，這里參與人“同時選擇”的是戰略，而不是行動。因為戰略是參與人行動的全面計劃，戰略式表述也可以描述動態博弈［13］。

在乒乓球戰術博弈過程中，參與人個數等于表的維度。顯然乒乓球戰術行為博弈參與人為雙方運動員，所以發球－接發球博弈的博弈矩陣表的維度是二維。矩陣表中的行和列上的文字表示了兩個參與人可選擇的策略，所以矩陣表的規模是由參與人的策略數量決定的。表中的每個單元格列出了相應策略組合下各參與人的得益。

下面博弈矩陣表提供的信息有（如圖5所示）:博弈雙方（發球方）和（接發球方）；博弈方所擁有的策略集合為旋轉發球和不轉發球兩種；表中前一個數字代表了博弈方的相應得益。對應的，博弈方擁有的策略集合為控制和進攻兩種接發球策略；表中的后一個數字代表了博弈方的得益。

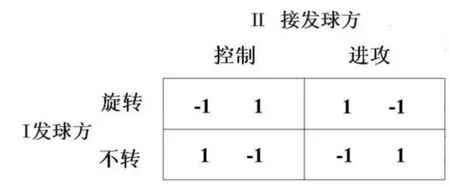
圖5 發球－接發球戰術行為博弈戰略式表述

4.2 乒乓球戰術行為博弈的擴展式表述

博弈的擴展式表述（extensive form representation）更適用于描述和分析動態博弈。博弈的擴展式表述所“擴展”的主要是參與人的戰略空間。戰略式表述簡單地給出參與人有些什么戰略可以選擇，而擴展式表述要給出每個戰略的動態描述:誰在什么時候行動，每次行動時有些什么具體行動可供選擇，以及知道些什么。簡單地說，在擴展式表述中，戰略對應于參與人的相機行動規則（contingent action plan），即什么情況下選擇什么行動，而不是簡單的，與環境無關的行動選擇［13］。

如圖6給出了發球－接發球序貫行動博弈的樹形圖。這個博弈有兩個參與人與參與人，假設參與人獲得了發球權，即戰術行動的發起者在圖的最左端的結點（node）上表達出這個含義即發球，該結點被稱作博弈樹的初始結（initial mode）或者根（root）。同時也可以稱作為行動結（action node）或決策結（decision node）在此結點有兩個可選擇的戰術行為分別用“發旋轉球”和“發不轉球”加以標明，并用從初始結發出的枝（branch）來加以表示。現在接發球方開始在新的結點上行動了，在的結點上分別也有兩個戰術行為可以進行選擇“控制”和“進攻”。沿著每條路徑都存在一個最后的結點，即終結點（terminal node）。在該結點，所有參與人不再進行行動選擇（注意終結點與行動結是不同的），表示了這些特定行動序列的結果即參與人的得益。

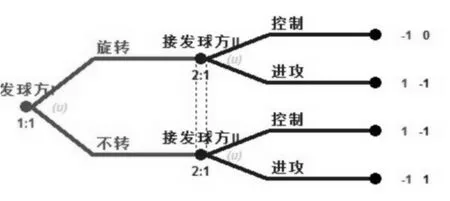
圖6 發球－接發球戰術行為博弈擴展式表述

5 乒乓球戰術行為博弈的求解方法

5.1 戰略式博弈模型的求解方法

劣策略概念及其提出劣策略涉及到博弈論的公理基礎。只有在博弈論中把局中人是完全理性的共同知識盡可能的公理化（Binmore，1992），運用歸納方法為博弈論構建堅實的基礎，使它成為可信賴的工具，那么博弈中局中人在個人理性假設下，可以相對定義劣策略，并且拒絕嚴格劣策略成為理性 選 擇 的 必 要 條 件 （Weirich，1998［14，15］）。 進 一 步，把Nash均衡作為非合作博弈中最基本的解，才會有兩個基本結論:①嚴格剔除劣策略過程中不會消去Nash均衡；②重復剔除劣策略過程后剩下的最后唯一的策略組合（即重復剔除的占優均衡）是Nash均衡。事實上，重復剔除嚴格劣策略是均衡的精煉（即對概念詳細區分的）過程（武康平，2001）。所以重復剔除劣策略成為分析博弈和尋找Nash均衡的基本方法之一。在圍繞博弈論基本概念發展中，D.Berhemi（1984）和D.Pearce（1984）在假設局中人是貝葉斯優化者為共同知識假設下導出了被占優策略的重復剔除。占優策略均衡、重復剔除的占優均衡、Nash均衡在非合作博弈論中作為主要的概念其關系也得到了揭示（張維迎，1996［16，17］。

5.2 擴展式博弈模型的求解方法

極小極大算法（minimax algorithm）是為博弈中的一方尋找一個最優行動方案的方法［18］。為了找到當前的最優行動方案，需要對各個行動方案可能產生的后果進行比較。具體地說，就是要考慮每一方案實施后對方可能采取的所有行動，并計算可能的分值。為計算分值，需要定義一個估值函數，用來估算當前博弈樹葉節點的分值。當葉節點的估值計算出來后，再推算出父節點的分值。推算的方法是，對于“或”節點，選其子節點中一個最大的分值作為父節點的分值，這是為了使自己在可供選擇的方案中選出一個對自己最有利的方案；對于“與”節點，選其子節點中一個最小的分值作為父節點的分值，即考慮最壞的情況。如果一個行動方案獲得較大的倒推值，則它就是當前最好的行動方案。為了表述方便，我們將取極大值的一方稱為Max方，另一方稱為Min方。

6 結 論

6.1 乒乓球戰術行為博弈理論，即是關于乒乓球戰術行為合理運用的理論體系，是研究如何在乒乓球競賽實踐中戰勝對手，提高勝算，獲取比賽優勝的理論。乒乓球戰術行為博弈理論是以“博弈論”的基礎理論、思想方法去研究和探索乒乓球技戰術在競賽過程中合理運用的微觀問題的理論，探討在乒乓球運動競賽中如何去戰勝對手、提高勝算、獲取優勝的科學理論。

根據乒乓球比賽規則和戰術行為的交叉效應，乒乓球競賽戰術實施過程可以表示為相互作用的耦合系統。

6.2 乒乓球戰術行為博弈要素包括:參與人（players）、行動（action or moves）、信息）（information）戰略（strategy）、支付（payoff）、次序（order）結果（outcome）和均衡（equilibrium）。對一個乒乓球戰術行為博弈描述至少必須包括參與人、戰略和支付，而行動與信息則是建筑材料。參與人、行動、次序和結果結合起來稱為乒乓球戰術行為博弈的規則（rules of the game），我們的研究目的在于運用博弈的規則來確定并分析乒乓球戰術行為博弈的均衡。

6.3 乒乓球戰術行為的博弈類屬可從不同角度出發進行分類，從博弈的參與人數量角度上乒乓球戰術行為博弈是兩人博弈；從博弈的次序角度上可定義為序貫博弈；從博弈的得益特點角度為零和博弈；從博弈的次數角度為重復博弈；從博弈的信息角度可定義為完美但不完全信息博弈，乒乓球戰術行為博弈有著特定的博弈規則，雙方運動員必須遵守，并且規則對戰術行為的實施有著非常明顯的影響。乒乓球戰術行為的博弈類屬是確定其納什均衡的基本前提。

6.4 根據乒乓球戰術行為實施的特征，乒乓球戰術行為博弈模型的建構，可有兩種表示方法，如把戰術行為的博弈過程，看作是純策略同時行動博弈，那么就可以用博弈表也稱博弈矩陣或支付表來進行描述。如果把乒乓球戰術行為博弈中戰術行為博弈看作是序貫博弈，可以用博弈樹進行表示。這種樹型圖被稱作博弈的擴展式表示方法。

［1］李光久.博弈論基礎要點注釋與題解精編［M］.南京:江蘇大學出版社，2008:32－46.

［2］迪克西特·斯克絲.策略博弈［M］.蒲勇健，等譯.第二版.北京:中國人民大學出版社，2009:68－74.

［3］李益群，謝亞龍.體育博弈論［M］.北京:北京體育大學出版社，2002:8－21.

［4］張曉蓬.中國乒乓球隊戰術訓練水平定量診斷方法及實踐效用［D］.中國優秀博碩士學位論文全文數據庫（博士），2004:25－36.

［5］張輝.球類比賽計算機診斷與分析［M］.哈爾濱:黑龍江科學技術出版社，2006:165－181.

［6］Shapley，Lioyd S.A Palue for N－Person Games［J］.grinceton University Press，1953（28）:307－17.

［7］唐建軍.乒乓球運動教程［M］.北京:北京體育大學出版社，2005:42－86.

［8］張輝，霍赫曼·安德烈亞斯.球類比賽數學模擬診斷的理論與實踐［J］.體育科學，2005（11）:3－5.

［9］G.Debreu，H.Scarf.A linit theorem on the core of an economy［M］.International Economic Review，1963:235－246.

［10］Von Neumann，J.，Morgenstern Oskar.Theory of games and economic behavior［M］.Princeton，1944:178－185.

［11］D.Kreps，R.Wilson.Sequential equilibria［M］.Econometrica，1982:863－894

［12］R.Selten.Reexamination of the perfectness concept for equilibrium points in extensive games［J］.International Journal of Game Theory，1975（4）:25－55.

［13］謝識予.經濟博弈論［M］.上海:復旦大學出版社，2002:9－31.

［14］Ken G.Binmore.A text on game theory［J］.Published Simultaneously in Canada，1992（4）:8－12.

［15］Weirich，Paul.Game theory revised by decision rules［J］.Cambridge University Press，1998（2）:7－10.

［16］張維迎.博弈論與信息經濟學［M］.上海:上海人民出版社，2004:27－38.

［17］約翰·納什［美］.納什博弈論論文集［M］.張良橋，王曉剛，譯.北京:首都經濟貿易大學出版社，2000:56－64.

［18］王騏.博弈樹搜索算法的研究及改進［D］.浙江大學，2006:25－32.