同信道干擾下相關多輸入多輸出信道容量分析
閆秋娜 岳殿武,2 王 謙
(1.大連海事大學信息科學技術學院,遼寧 大連116026;2.東南大學移動通信國家重點實驗室,江蘇 南京210096)
引 言
近年來,在發送端和接收端使用多個天線的多輸入多輸出(MIMO)無線通信系統由于極大地增加了信道容量,引起了廣泛的關注。關于無線MIMO系統,人們已在多個方面對其進行了深入的研究,尤其是在信道容量方面。然而,迄今為止對信道容量的分析還主要集中在沒有同信道干擾情況下的MIMO 系統[1]。
在蜂窩移動通信系統中,多個用戶由于共享同一個射頻頻譜因此不可避免的引入了同信道干擾,從而嚴重地影響了系統提供給用戶的服務質量。為此,不少學者開始對衰落環境下帶有同信道干擾的MIMO信道容量進行研究[2-5]。特別是,Kang等人推出了MIMO信道容量矩生成函數(MGF)、均值和方差的精確閉式表達式[3]。然而,他們所考慮的僅是在Rayleigh衰落環境下通信用戶的發送和接收天線陣都不相關的情況。在許多實際無線環境中,由于缺少散射條件,天線之間容易存在信號相關;此外,由于物理尺寸的限制,在移動終端使天線之間間隔較遠是非常困難的,因此,也會使天線之間存在著空間相關性。最近,Wang等人研究了通信用戶接收天線陣帶有空間相關性的情景,并在存在同信道干擾情況下獲得了MIMO Rayleigh衰落信道容量的分析結果[5]。
鑒于上述因素,本文側重研究帶有同信道干擾和發送相關的MIMO信道容量問題。主要針對通信用戶和同信道干擾用戶都處于Rayleigh衰落環境的情況。
復矩陣變量分布理論是本文所采用的主要分析工具。這個理論已經成功的用于不帶有干擾的MIMO信道容量分析中[1]。
1.矩陣變量的超幾何函數
1.1 矩陣變量超幾何函數的定義
許多矩陣變量分布,特別是中心二次型分布,都能表示成矩陣變量的超幾何函數形式[7-8]。矩陣變量的超幾何函數是單變量超幾何函數的一般化,而單變量的超幾何函數已經被廣泛地應用在科學與工程領域。下面給出復數域上矩陣變量超幾何函數的定義,并討論復矩陣變量超級幾何函數與單變量超級幾何函數之間的關系。
對于一個預先給定的正整數k,可用一個正整數向量k=(k1,k2,…,kp)表示k的一個劃分。對于一個劃分就意味著這些正整數分量之和為k.復多元的超幾何系數可表示為

式中:(x)n=x(x+1)…(x+n-1)是Pochhammer符號[7]。
定義1[7]令X是一個p×p的Hermitian矩陣。則復矩陣變量超幾何函數定義為

式中:a1,…,am;b1,…,bn是任意復數;表示對所有劃分k的求和;Ck(F)是關于k的F的帶狀(Zonal)多項式。
為了證明第3部分中提出的定理1,需要給出兩個矩陣變量的超幾何函數的定義,下述定義雖然和James在文獻[7]中所給出的定義在形式有些不同,但在本質上是一樣的,就像在文獻[1,8]中所使用的那樣。
定義2[7-8]令p≤q,涉及兩個 Hermitian矩陣X(p×p)和Y(q×q)的超幾何函數定義為

式中各種符號所表示的含義同定義1,其詳細討論可參考文獻[1,9]。
1.2 基于單變量超幾何函數的表達式
矩陣變量的超級幾何函數雖然便于理論上的分析,但不方便進行實際的數值計算。為此,討論其與便于數值計算的單變量超級幾何函數之間的關系。
一般Hermitian矩陣變量超幾何函數可以由單變量超幾何函數來表示。
一個p×p的對角矩陣Λ =diag(λ1,λ2,…,λp),(λ1>λ2>…>λp)的Vandermonde矩陣可表示為

引理1[1]令B是一個p×p的Hermitian矩陣。定義 Θ=eig(B)=diag(ω1,…,ωp),ω1> …>ωp,則關于矩陣B的超幾何函數可表示為

式中:F=[fij],i,j=1,2,…,p,且該矩陣中元素可表示為單變量超幾何函數:

如下面的引理2所述,兩個Hermitian矩陣變量的超幾何函數也能夠由單變量超幾何函數來表示。
引理2[1]令
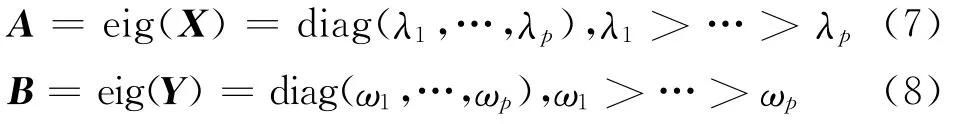
再定義
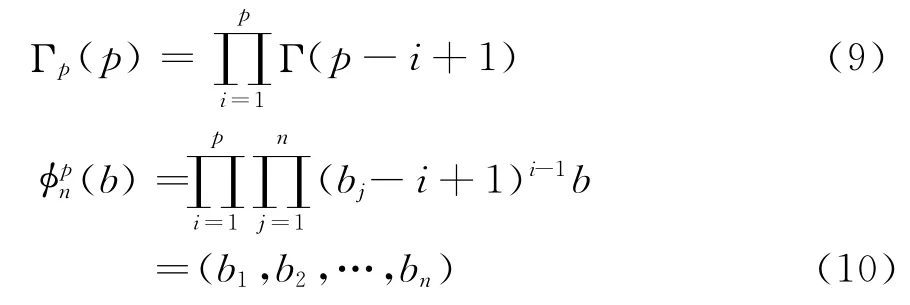
則

式中:L=[lij],i,j=1,2,…,p,且該矩陣中元素可表示為單變量超幾何函數:

引理1和引理2將會為矩陣變量超幾何函數的數值計算提供方便。
2.MIMO系統模型
考慮一個帶有t個發射天線和r個接收天線的無線通信系統。假定該系統是一個僅限干擾的系統,其加性噪聲因影響比較微弱,可以在分析中忽略。設有l個干擾用戶,每個干擾用戶具有ti(i=1,…,l)根干擾天線。接收端接收的r×1階向量可表示為

式中:H是服從高斯分布的r×t階歸一化信道復矩陣,H ~(0,Σ ?Ψ),Σ ?Ψ 是隨機矩陣H 的協方差矩陣(參見文獻[9]的第7章);s是一個t×1階的歸一化發射信號向量,且相關性為E(ss?)=Rs;Es是系統的總發射功率。同樣,對于第i個同信道干擾,Hi是r×ti階歸一化干擾信道矩陣,si是ti×1階干擾用戶發射信號向量,其平均功率為Ei,且可假定 Hi~CNr,t(0,Σi? Ψi),si~(0,Ri).
對于式(13)中的隨機矩陣H和Hi,現給出進一步說明。矩陣H和Hi的相關性分別由Σ?Ψ和Σi?Ψi表示。Σ和Σi分別表示在接收端輸入信號和干擾信號的r×r階相關矩陣。Ψ表示發射天線陣列的t×t階相關矩陣,而Ψi是第i個干擾的ti×ti階相關矩陣。這些矩陣與天線陣列的結構、信道的特性等因素密切相關。
為了簡明起見,和文獻[2-5]類似,對接收機,其上所有的干擾信號si(i=1,…,l)都假定是不可知的,且都為復高斯向量。因此,在Hi(i=1,…,l)為已知的條件下,干擾為復高斯的,其協方差矩陣為

式中:

為了便于分析處理,首先假定Σ1=Σ2=…=Σl=Σ.注意 .這個假定的約束條件比起文獻[2-4]更為寬松些。因為在這些文獻中除了約束所有干擾的相關接收矩陣都是相同的之外,還要滿足Σ1=Σ2=…=Σl=I.為了得到簡化的閉式表達式,現進一步假設[5-6]

此外,還要假設接收端完美地知道信道狀態信息,而發送端不知道。那么當發射信號不相關,即Rs=It時,系統能夠獲得最大瞬時容量,這時Rs是最優的。為此,可假定Rs=It,同時也假定

在上述所有的假設下,下面推導隨機矩陣ρH?(Hi)-1H的統計表達式。其中

3.帶有干擾的MIMO信道容量
3.1 矩生成函數和遍歷容量
對于MIMO信道的輸入向量s和式(11)給出的輸出向量y,其瞬時互信息I(s,y)的表達式為[2-5]

式中

令

CNr,tI(0,Ir?ItI)。則根據文獻[9]中的定理7.4.1的證明,Q又可以表示為

于是MIMO信道的遍歷容量可表示為

進一步互信息I(s,y)的矩生成函數可表示為

那么通過式(26)就可求得遍歷容量[5]。

3.2 矩生成函數表達式
定理1 假設通信用戶接收端天線數小于或等于所有干擾用戶發射端天線數之和,即r≤tI,則互信息I(s,y)的矩生成函數可表示為


定理1之證明見附錄A。
為了便于數學處理,在MIMO系統的性能分析中通常要采用r≤tI的假設[3,5-6]。這個假設特別符合移動通信下行傳輸情況,因為體積小、重量輕的手提或便攜式發送終端實際上只能安裝一兩個天線。
3.3 MIMO信道的遍歷容量
現給出基于單變量超幾何函數的MIMO系統遍歷容量表達式。
定理2 假設r≤t1,并令Λ =eig(It-)=diag(λ1,λ2,…,λt),λ1<λ2< … <λt。則 MIMO遍歷容量可表示為

式中

定理2之證明見附錄B.
4.數值結果
下面要用數值結果驗證分析結論的正確性,討論各種系統參數對MIMO系統遍歷容量的影響,并與已有的文獻結果[4-5]進行比較。
為了簡明起見,只利用文獻[12]中的指數模型來描述發送端和接收端天線之間的相關性:

式中gr和gt分別表示接收端和發送端天線陣的相關系數,范圍從0到1,增加表示天線之間的相關性增強。
將發送端天線之間和接收端天線之間的相關系數分別設置為0.1和0.5,然后固定發送端天線數目為2.在圖1中,對不同的接收端天線數目和總干擾發送天線數目下的信道容量理論分析結果進行蒙特卡羅仿真驗證。為了使統計結果可靠,蒙特卡羅仿真實驗次數取定為106,以下同。從圖1可以看出,理論數值結果和蒙特卡羅仿真結果非常匹配,從而驗證了理論分析結果的正確性。
在圖2中,對不同的發送端天線陣相關系數下的信道容量進行數值比較。為了公正的比較,其他參數的設置相同,即t=2,r=3,tI=4,gr=0.5.從圖2可以發現,理論結果和仿真結果非常符合,且相關性越高,容量越小,這符合MIMO空間相關性對性能負面影響的特征。并且還可以看出,強的空間相關性對遍歷容量的影響是非常大的,尤其是在高信干比的區域。

圖2 不同發送端天線陣相關系數信道容量與ρ的關系曲線
在圖3中,對不同的總干擾發射天線數目下的信道容量進行了比較。圖中信干比(SIR)是接收信號和干擾信號功率之比,可表示為


圖3 不同總干擾發射天線數目下信干比的信道容量
從圖3可以看出,當干擾天線的數量增加時,容量會降低,但降低的幅度逐漸變小。這是因為在同樣條件下干擾天線的數量多比數量少所形成的干擾統計方差會更高些,但隨著數量增多,該方差也逐漸收斂到一個固定值。
在干擾天線數tI=4、發送天線數t=4和接收天線數r=4情況下,圖4比較了發送空間相關性和接收空間相關性對遍歷信道容量的影響。圖4共畫了四條曲線,其中兩條曲線對應發送相關參數取gt=0.2,0.6兩種情況,而其他兩條對應接收相關參數取gr=0.2,0.6兩種情況。從圖4可見,盡管空間相關性參數選取一樣,發送相關性和接收相關性都對遍歷信道容量產生影響,但發送空間相關性隨著相關參數增加對遍歷信道容量影響越來越嚴重,且明顯超過接收空間相關性的影響。

圖4 發送相關性和接收相關性對遍歷信道容量的影響比較
在干擾天線數tI=6和接收天線數r=3情況下,對于不同發送天線數目,圖5側重比較了有和沒有發送空間相關性對遍歷信道容量的影響。圖5對比了t=2,4,6三種情況。從圖5可見,隨著發送天線數增加,不論有沒有空間相關性,遍歷容量均越來越大。空間相關性雖然會使遍歷容量有所影響,但這影響并不隨發送天線數變化而明顯發生變化。
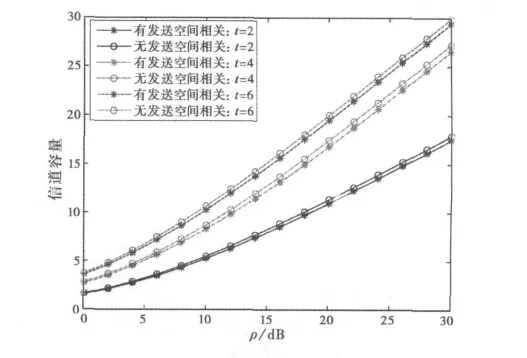
圖5 不同發送天線數目下發送空間相關性對遍歷信道容量的影響
在發送天線數t=3和接收天線數r=3情況下,圖6比較了同信道干擾和發送空間相關性對遍歷信道容量的影響。圖6中虛線表示沒有干擾也沒有空間相關性情況,其他四條曲線中臨近虛線的兩條曲線對應相關參數取gt=0.6,0.9兩種情況,另外兩條對應干擾天線數取tI=6,9兩種情況。從圖6可見,盡管同信道干擾和發送空間相關性都對遍歷信道容量產生影響,但空間相關性影響是有限的,而同信道干擾隨著干擾天線數目增加越來越嚴重,明顯超過空間相關性的影響。

圖6 同信道干擾與發送空間相關性對遍歷信道容量的影響比較
5.結 論
在Rayleigh衰落環境下,深入地研究了具有同信道干擾和發射空間相關性的MIMO信道容量問題。在假定當接收端完美地知道信道狀態信息而發射方不知道情況下,利用矩陣變量分布理論,首先推導出MIMO信道互信息的矩生成函數的精確閉式表達式,然后通過該表達式可進一步得到MIMO遍歷容量的精確表達式。可見,對MIMO衰落信道容量的分析在很大程度上要依賴于矩陣變量分布理論。
由于數學處理的難度,在系統模型中還不得不加入了一些限制和約束。因此,就一般模型而言,帶有同信道干擾和空間相關性的MIMO信道容量問題依然是一個沒有徹底解決的困難問題。這將需要更復雜、更有力的數學工具來幫助解決。
[1]KIESSLING M.Unifying analysis of ergodic MIMO capacity in correlated Rayleigh fading environments[J].European Transactions on Telecommunications,2005,16(1):17-35.
[2]KANG M,YANG L,ALOUINI M S.Performance analysis of MIMO channels in presence of co-channel interference and additive Gaussian noise[C]//Proc the 35th Annual Conference on Information Sciences and Systems.Baltimore,2003.
[3]KANG M,ALOUINI M S.Capacity of MIMO Rician channels with multiple correlated Rayleigh co-channel interferers[C]//Proc IEEE Global Telecommun Conf.San Francisco,2003:1119-1123.
[4]KANG M,YANG L,ALOUINI M S.Capacity of MIMO channel in the presence of co-channel interference[J].Wireless Communications and Mobile Computing,2007,7(1):113-125.
[5]WANG Y,YUE D W.Capacity of MIMO Rayleigh fading channels in the presence of interference and receive correlation[J].IEEE Transaction on Vehicular Technology,2009,58(8):4398-4405.
[6]KANG M,ALOUINI M S.Quadratic forms in complex Gaussian matrices and performance analysis of MIMO systems with co-channel interference[J].IEEE Transaction on Wireless Communications,2004,3(2):418-431.
[7]JAMES A T.Distributions of matrix variates and latent roots derived from normal samples[J].Ann Math Stat,1964,35(2):475-501.
[8]KHATRI C G.On the certain distribution problems based on positive definite quadratic functions in normal vectors[J].Ann Math Statist,1966,37(2):468-479.
[9]GUPTA A K,NAGAR D K.Matrix Variate Distributions[M].NewYork:Chapman& Hall/CRC,2000.
[10]KHATRI C G.Classical statistical analysis based on a certain multivariate complex Gaussian distribution[J].Ann Math Statist,1965,36(1):98-114.
[11]CHIANI M,WIN M Z,ZANELLA A.On the capacity of spatially correlated MIMO Rayleigh-fading channels[J].IEEE Trans Inform Theory,2003,49(10):2363-2371.
[12]ZHANG Q T,CUI X W.Outage probability for optimum combining of arbitrarily faded signals in the presence of correlated Rayleigh interferers[J].IEEE Transactions on Vehicular Technology,2004,53(4):1043-1051.
[13]YAN Q N,YUE D W.Matrix variate distributions and MIMO channel capacity[C]// Conference Proceedings of 2009International Institute of Applied Statistics Studies.Qingdao,China,2009:386-394.

