小樣本條件下一種旋轉機械振動狀態閾值的確定方法及應用

李會鵬 明廷鋒 賀 國

（海軍工程大學船舶與動力學院 武漢 430033）

振動是影響大型旋轉機械安全運行的重要因素，因此對旋轉機械的振動監測可及時發現問題，有效保障設備的安全運行.自助法和隨機加權法都是利用樣本重采樣技術進行樣本擴充的方法［1－3］.經仿真計算和實際應用表明，隨機加權法較自助法有更高的精確度［4］.然而，這兩種方法對樣本信息依賴較大，若直接運用該方法對樣本進行擴充，可能會產生較大的誤差.本文綜合運用隨機加權法、Bayes方法和信息融合方法，對小樣本條件下振動閾值的設定方法進行研究，以期最好地解決小樣本條件下的閾值設定問題.

1 特征值的均值與方差估計方法

1.1 隨機加權法

設未知參數α服從正態分布，大小相互獨立.記α＝（x1，x2，…，xn）為現場子樣，μ和σ2分別為α的均值和方差，運用隨機加權法估計μ和σ2，具體步驟如下.

1）計算現場子樣的均值ˉx和方差s2，即有：

2）產生N 組Diricklet隨機向量，V（i）＝（Vi1，Vi2，…，Vin），i＝1，2，…，N，這里（Vi1，Vi2，…，Vin）為參數（1，1，…，1）的 Diricklet隨機向量，記它的聯合分布為（1，1，…，1）.它可按如下方法產生：

設v1，v2，…，vn－1是（0，1）上均勻分布的隨機變量v的獨立同分布子樣，對其按從小到大的次序重新排序，記為v1≤v2≤…≤vn－1.又記v0＝0，vn＝n，Vij＝vj－vj－1，j＝1，2，…，n.那么，（Vi1，Vi2，…，Vin）的聯合分布就是（1，1，…，1）.它就是所需的Diricklet隨機向量.

分布參數μ，σ2的均值估計分別為

1.2 驗前分布的信息融合

式中：wi為第i個信息源的權重因子＝1.

樣本方差

1.3 Bayes統計推斷方法

在正態分布條件下，未知參數β的均值μ與方差σ2的聯合共軛分布是正態－逆Gamma分布，即（μ，σ2）～N－IGa.式中：μπ，kπ，為共軛先驗分布∏（θ）的超參數.根據文獻［8－9］可以得出以下結論.

1）（μ，σ2）的后驗分布也是正態 －逆 Gamma分布 N－IGa.

2）μ的后驗分布是自由度為vk的學生氏分布），即μ／

3）σ2的后驗分布是逆Gamma分布

2 小樣本條件下特征值的統計參數估計方法

結合上述分析和旋轉機械振動的特征值－振動有效值分布規律，根據數理統計分析的基本理論和一般步驟，綜合運用Bayes方法、信息融合方法和隨機加權法，得到振動有效值分布特性統計參數估計流程，見圖1.

圖1 小樣本下旋轉機械振動特征值的統計參數估計流程

該流程的主要思路是：首先對n組樣本的數據量進行判斷，若樣本數小于20，運用小樣本統計方法.其次，利用專家經驗對各個小樣本進行判斷，選擇正常的樣本進行小樣本統計運算；再次，判斷正常樣本是屬于現場樣本還是屬于歷史樣本：若樣本屬于現場樣本，則通過隨機加權法可以得到現場樣本的分布；若樣本屬于歷史樣本，則利用隨機加權法可以得到先驗分布.在得到各個歷史樣本的先驗分布的基礎上，運用信息融合方法對各個樣本信息進行信息融合得出樣本信息的驗前分布；最后運用Bayes統計推斷方法進行后驗推斷，獲得所需參數的特征值估計，再依據3σ方法設定合適的閾值.

3 仿真研究

3.1 隨機加權法估計樣本的均值與方差

根據1.1中隨機加權法對其均值和方差的分布情況進行估計：樣本M 均值μM～N（14.33，0.462），方差σ2M～N（2.13，1.342）；樣本 N 均值μN～N（14.79，0.612），方 差～N（3.76，1.732）；樣本Q均值μQ～N（15.36，0.682），方差～N（4.44，1.362）.

3.2 歷史樣本的信息融合

根據1.2中先驗信息融合方法計算得到：w1＝0.599 0，w2＝0.401 0.

那么，樣本信息融合后均值

同理，得方差ˉσ2～N（2.78，1.512）.

3.3 特征值統計參數的Bayes推斷方法

令μ的先驗分布表示為∏（μ），σ2的先驗分布表示為∏（σ2）.由3.2的計算，得∏（μ）先驗均值為＝14.51，先驗方差為＝0.532；∏（σ2）的先驗均值為＝2.78，先驗方差為＝1.512.

根據1.3中的結論2和結論3的建立以下2組方程組

將上面兩方程組聯立，求得先驗分布的超參數為

由1.3中的結論4，求得后驗分布超參數為

因此μ的后驗期望估計為

運用隨機加權法、信息融合方法和Bayes統計推斷獲得參數的分布估計為N（14.89，4.00）.定義該方法為Bayes－隨機加權法.將該方法與經典統計、隨機加權法進行對比，見表1.

表1 統計參數估計結果對比

分析表1，隨機加權法與經典統計法相比，它的方差估計值更小，其均值估計值變化不大.而Bayes后驗推斷融合了先驗分布和現場信息進行后驗估計，使得計算出后驗估計的均值和方差更加逼近期望，它對均值估計值與期望值非常接近，它對方差的估計值與期望值一致，取得了較理想的結果.由此可見，本文給出的Bayes－隨機加權法對小樣本統計特征推斷有一定的優越性.

4 實例應用

對一臺離心泵機組故障模擬平臺的振動狀態進行監測.現有歷史樣本A，B和C，分別為：樣本A（31.50，32.95，28.50，30.84，30.16，32.71），樣本B（22.82，22.96，23.67，21.92，21.67，22.69），樣本C（23.97，23.65，23.77，25.03，22.93，24.54）.并有現場樣本D（23.46，25.59，25.96，24.86，24.08，25.23），上述樣本振動數據均為該離心泵機組水平方向加速度振動有效值，單位為mm／s2.

4.1 樣本信息的均值與方差估計

根據1.1中隨機加權法計算得到樣本A均值μA～N（31.10，0.572），方差～N（2.78，0.852）；樣本B 均值μB～N（22.62，0.252），方差～N（0.53，0.162）；樣 本 C 均 值 μC～N （23.98，0.252），方差～N（0.53，0.172）；樣本D 的均值μD～N（24.86，0.332），方差～N（0.89，0.252）.

4.2 先驗信息的分析與融合

依據專家經驗知悉該離心泵機組故障具有“浴盆曲線”特性，見圖2，起始段故障率較高，為磨合期，經過一段時間后，故障率減小，為偶發期，隨著運行時間的增加故障率開始增加，即為耗損期.

圖2 離心泵機組故障概率模型圖

依據圖2所示設備故障概率模型圖，對先驗樣本A，B和C進行分析，可知樣本A的振動數據偏大.結合該監測樣本的獲取時機恰好是在設備剛投入使用不久.根據圖2知，該設備正處于磨合期，因此振動較大，波動也較為明顯；而樣本B和C的振動較為平穩，波動較小.因此，在選擇先驗樣本時，為避免振動閾值設定不合理，應把樣本A舍去，僅選用樣本B和C作為先驗信息.

根據1.2中先驗信息融合方法.計算wi得到：w1＝0.502 4，w2＝0.497 6.

那么，樣本信息融合后均值

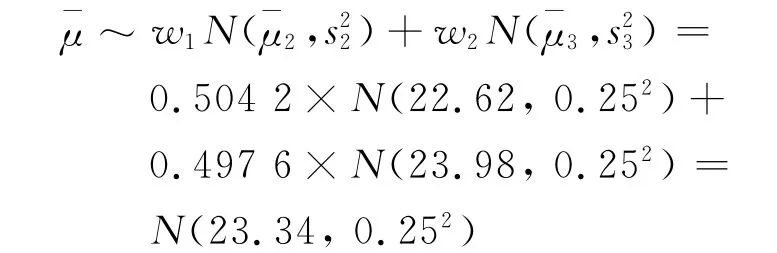
同理可得樣本信息融合后方差ˉσ2～N（0.53，0.162）.

4.3 Bayes統計推斷方法估計統計參數

計算過程與3.3一致，得μ的后驗期望估計為

4.4 振動有效值的閾值設定

通常，設備振動較小時不認為是故障狀態，所以只需設定報警上限，而不用設定報警下限.根據閾值評定準則，可求出閾值的報警限：

同理，隨機加權法設定的報警閾值為27.53，利用經典統計法設定的報警閾值為27.68，單位均為mm／s2.

現模擬離心泵機組的地腳螺栓松動故障，測取并計算得到10組故障樣本（水平向加速度振動有效值）：G（30.17，27.61，28.72，27.16，28.68，29.46，28.08，29.43，26.93，31.64），單位為mm／s2.分別利用Bayes－隨機加權法、隨機加權法和經典統計法設定報警閾值，結果見圖3.

圖3 離心泵機組水平向振動有效值報警線圖

從圖3可以看出：應用Bayes－隨機加權法設定的報警線沒有出現誤報和漏報的情況，應用隨機加權法設定的報警線出現2次漏報，應用經典統計方法設定的報警線出現3次漏報.由此可見，本文給出的振動狀態閾值設定方法因為融合了驗前信息，所制定的報警線更加的科學，得到最好的效果，而應用隨機加權法制定的報警效果稍差，應用經典統計制定的報警效果最差.

5 結 論

1）隨機加權法適用于小樣本條件下的樣本擴充，與傳統的數理統計相比，得出的統計參數的分布的估計精度更高，但該方法對樣本本身的信息依賴性較大，容易受樣本信息的波動而波動，造成估計精度誤差較大.

2）信息融合方法有效解決了來自不同分布數據的合理利用問題，該方法根據樣本數據的穩定性大小合理的設定權重值.當樣本數據的穩定性好時權重值設定較大，反之權重值就較小.

3）綜合運用隨機加權法、信息融合技術和貝葉斯方法進行參數的統計推斷，得出的推斷參數值合理和穩定，可彌補隨機加權法的不足.

4）將Bayes－隨機加權法應用到小樣本條件下的某離心泵機組整機振動閾值的設定.結果證明設定的閾值合理、有效.

［1］EFRON B.Bootstrap methods：another look at the jacknife［J］.The Annals of Statistics，1979，7（1）：1－26.

［2］DONALD B R.The bayesian bootstrap［J］.Annals of Statistics，1981，9：130－134.

［3］鄭忠國.隨機加權法［J］.應用數學學報，1987，10（2）：247－253.

［4］張湘平，張金槐，謝紅衛.基于隨機加權法的BAYES精度評定［J］.國防科技大學學報，2001，23（3）：98－102.

［5］張 喆，馮 靜.基于混合驗前分布的小子樣維修性驗證試驗方法研究［J］，兵工自動化，2010，29（2）：27－29.

［6］張堯庭，陳漢峰.貝葉斯統計推斷［M］.北京：科學出版社，1991.

［7］陳小佳，沈成武.既有橋梁的貝葉斯網絡評估方法［J］.武漢理工大學學報：交通科學與工程版，2006，30（1）：132－135

［8］戚宗鋒.電子裝備小子樣試驗方法研究［D］.長沙：國防科學技術大學，2002.

［9］陳春良，石 全，張會奇，等.AHP－Bayes及Bootstrap方法在戰損裝備維修工作量統計建模中的應用［J］.裝甲兵工程學院學報，2009，23（2）：5－8.

［10］盛 聚，謝式千，潘承毅.概率論與數理統計［M］.3版.北京：高等教育出版社，2003.