黃沙吹盡 返璞歸真——一道習題的多角度探究

☉湖北省宜昌市夷陵中學 徐 勇

學生上完選修4-5《不等式選講》第二講“柯西不等式”不久，一個學生拿著一道題來問我，原題如下：

我和這名同學一起分析，覺得要求出u的最小值，去根號是關鍵，于是有了如下探究：

探究一：由柯西不等式（a2+b2）（c2+d2）≥（ac+bd）2得：

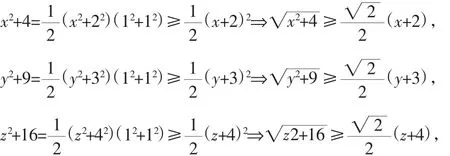
探究二：

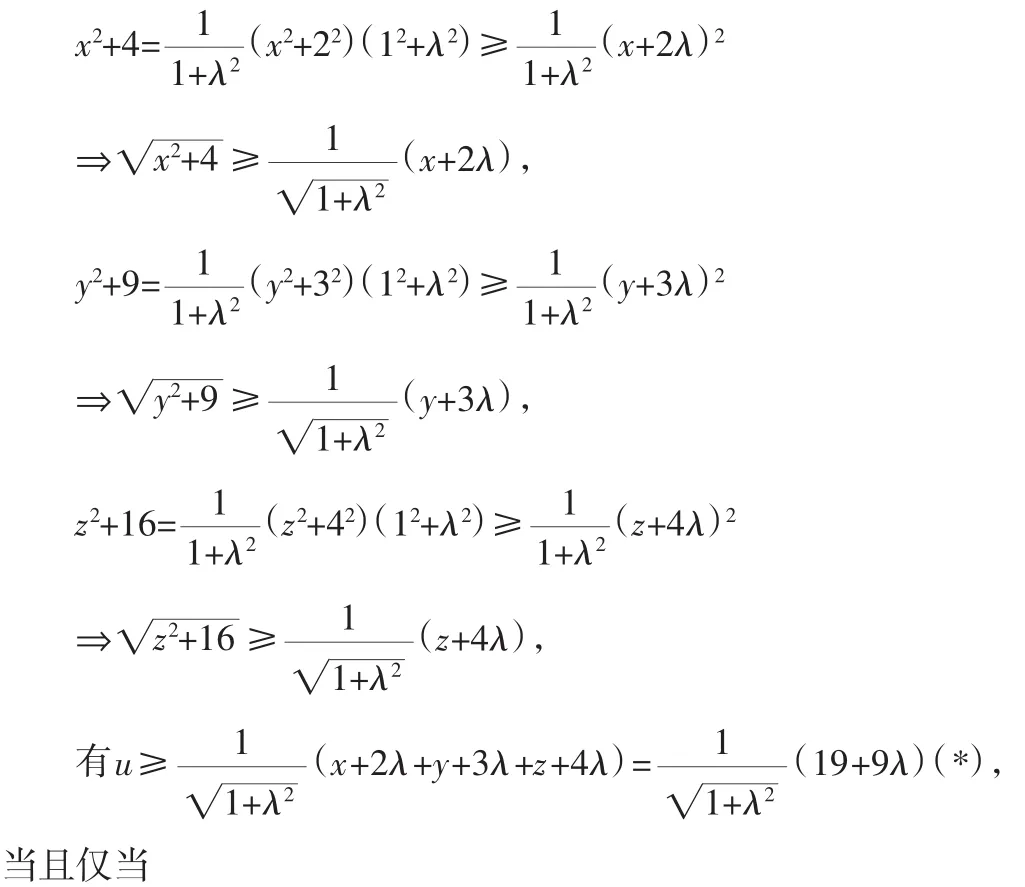
和學生一起探究完這道題，感覺這道題能很好地培養學生的觀察、分析、辨誤、糾誤能力，是一道難得的好題，于是決定在習題課上面向全班學生評析此題.

第二天的習題課上，當我按照上面的探究一、探究二講解完這道題，并再次強調此題構造柯西不等式的思路時，幾個學生在下面小聲說，這樣構造也太麻煩了吧！這句話打消了我接著講下一題的計劃.是啊，像探究一、二這樣做確實能解決問題，但付出的代價太大了，還不如發揮學生的主體地位，讓學生繼續探究下去！于是，我引導道：“還有沒有更簡單的方法？請大家思考并討論.”經過熱烈的討論，不少同學舉起了手，我點了學生甲，請他到黑板前面讓大家分享他的成果，于是有了如下探究：

探究三：考慮到柯西不等式左邊有兩組平方和相乘，而本題的函數u為三項相加，只要先把u平方即可得到乘積形式，即u2=x2+4+y2+9+z2+16+2 ［8）=（x+y+z）2+81=442，當且僅時等號成立.又u＞0，故umin=

教室里響起了熱烈的掌聲！探究三充分考慮了柯西不等式的結構特點，求解更為直接.那這道題還有沒有別的做法呢？這時學生的思維完全打開了，不久學生乙就給出了另一種方法：

探究四：本題函數u為根式和形式，且被開方數為平方和形式，這一點與二維形式的三角不等式吻合，所以連續兩次運用三角不等式即可，

學生乙的做法跳出了柯西不等式的窠臼，根據函數式的整體結構特點進行有效聯想，做法漂亮、干脆，令人眼前一亮！當大家還沉浸在這種優美解法中時，學生丙舉手站了起來：

探究五：探究四的做法實質就是構造三個向量：a=（x，2），b=（y，3），c=（z，4），，當且僅當向量a，b，c同向共線，即時兩等號同時成立.故u

好一句“實質就是”，讓我們對函數u有了新的認識.那我們對函數u還能從別的角度去認識它嗎？果真是“思想有多遠，行動就有多遠”，很快學生們就給出了另一種探究思路：

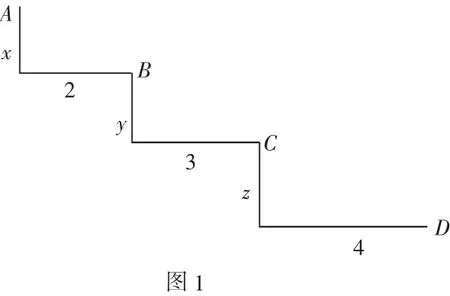
由兩點間線段最短有

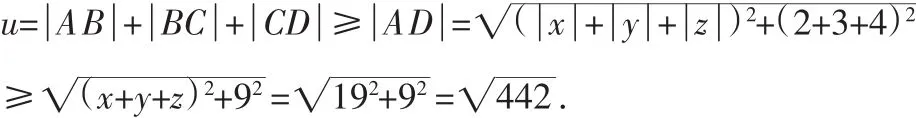
真是令人拍案叫絕！一道看似需要用柯西不等式才能做的問題，竟然用初中的平面幾何知識就輕易解決了！學生們徹底沸騰了……

反思：很多學生包括老師在內都有一種思維定勢，認為新課后的作業、習題一定要用新課上的知識去解決，這種觀點其實是大錯特錯的.本案例中，通過放手發動學生去思考，學生不斷優化自己的思維，在創造、再創造中得出很多體現了書本知識靈活應用的方法，逐步對問題的本質有了清晰的認識.另外，本次探究成功很重要的一點是有了學生的積極參與.布魯納認為：在教學過程中，學生是一個積極的探索者，教師的作用是形成有助于學生獨立探究的情境，讓學生自己思考問題，參與知識獲得的過程.教師要舍得留出時間和空間給學生，以供他們馳騁自己的思維.