基于矩陣的電子公文加密解密方法
張善文, 王保倉, 周爭光
(西京學院工程技術系,西安 710123)
0 引言
隨著電子公文的廣泛應用和不斷發展,一方面是資源的節約和工作效率的極大提高;另一方面是電子公文的安全性問題[1-2]。實際上,在電子公文投入應用之日起安全問題就隨之而來。例如,如何保障電子公文的真實性和來源的可靠性以及文件如何存檔,如何確定發送者身份的真實性,如何保障文件數據的完整性,如何防止發送者的不可抵賴性等。電子公文同其他電子文檔一樣可能會遭遇偽造、篡改、增刪、冒名等;電子公文又與傳統紙質文件不同,電子公文載體具有易損、信息易變、形式多樣和記錄虛化等特點,形成后必須及時、妥善地加以管理,否則可能對日后的檔案完整性造成無法挽回的損失。因此,如何保證電子公文的安全性是政府部門電子政務發展的重要內容。現在,電子公文傳送過程中數據的安全性是通過加密和數字簽名或數字水印來實現的[1-6]。公開密鑰基礎設施(PKI)是通過使用公開密鑰技術和數字證書來確保電子公文系統信息安全并負責身份驗證的一種有效方法[3],但該體系存在一些不足:1)私鑰安全性難以保證,私鑰是一組數字串,一旦被竊取,數據發送方的身份將無法準確鑒別,可追溯性也難以保證;2)認證信息和電子公文的分離,不利于電子公文的交換和長期保存。采用數字水印技術可以實現電子公文安全系統,其優點在于它能夠很好地對文檔的完整性進行驗證。由于電子公文載體的特殊性造成了文本數字水印技術上的困難,而水印算法的安全性不能依靠保密水印算法來實現,所以大多數水印算法都是公開的,一旦水印算法被公開,所有采用該方法加密的電子公文可能面臨來源不可靠的風險。常用的公鑰密碼算法其安全性都是基于數論上的困難問題,如分解大整數和求解特定循環群上的離散對數問題。已經證明整數分解和離散對數問題可以使用量子計算機在多項式時間內解決,為了消除量子計算機的實際實現所帶來的潛在威脅,人們希望設計更多解決別的數學困難問題的公鑰密碼算法[7-8]。基于組合問題的公鑰密碼的設計與分析是目前研究的一個熱點,本文提出一種基于組合矩陣的電子公文加密方法。
1 電子公文的安全傳輸和接收
電子公文系統的安全性主要包括公文數據傳輸流程設計、身份識辨、電子排版、電子蓋章及印章管理、全程加密、遠程傳版、收發文審計管理和可開放定制等,將電子公文傳輸方式從傳統的“先打印后發送”更改為安全的“先傳輸后打印”模式,從而達到既能用計算機網絡安全傳輸紅頭文件,又基本不改變現有工作流程的目的,并解決相應帶來的遠程傳版、電子公章管理、系統安全性、電子公文有效性等問題[1-2,4-6]。下文給出電子公文安全傳輸和發收方案如圖1~圖4所示。
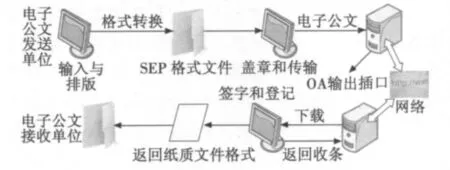
圖1 電子公文發送和接收系統流程圖Fig.1 Flowchart of electronic document sending and receipting system
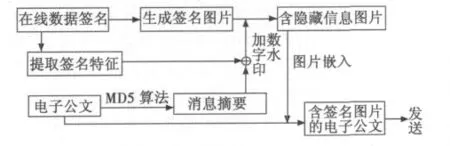
圖2 電子公文水印加密發送流程圖Fig.2 Watermarking transceiver encryption flowchart of electronic documents
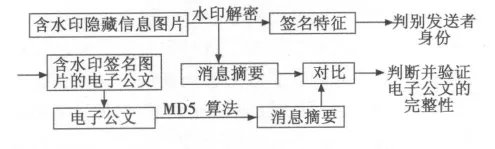
圖3 電子公文水印接收解密流程圖Fig.3 Watermarking transceiver decryption flowchart of electronic documents
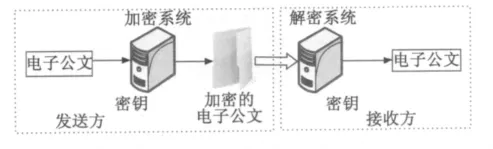
圖4 電子公文加密系統Fig.4 Symmetric encryption of electronic documents
其中:圖1為電子公文的傳輸示意圖;圖2為電子公文水印加密發送流程;圖3為電子公文水印接收解密流程圖;圖4為一般電子公文加密系統框圖。
2 電子公文的加密方法
基于矩陣的電子公文安全性發收方案包括3部分:密鑰生成、加密、解密和參數選取[9-12]。
1)密鑰生成。密鑰生成方法所涉及到的矩陣的維數記為n,在實際應用過程中一般選取n=4。一對公鑰和私鑰按如下方式產生:隨機選取一個1024 RSA模數N=pq,其中p和q是素數,則|p|2=|q|2=512。隨機選取一個n維矩陣 A:A=(aij)n×n,其中,aij為矩陣A的任意一個元素,且矩陣A在R上是可逆的,它的逆矩陣記作A-1。再隨機選取4個矩陣C、D、E、F:使得 aij,cij,dij,eij,fij∈ZN,滿足下面兩個條件
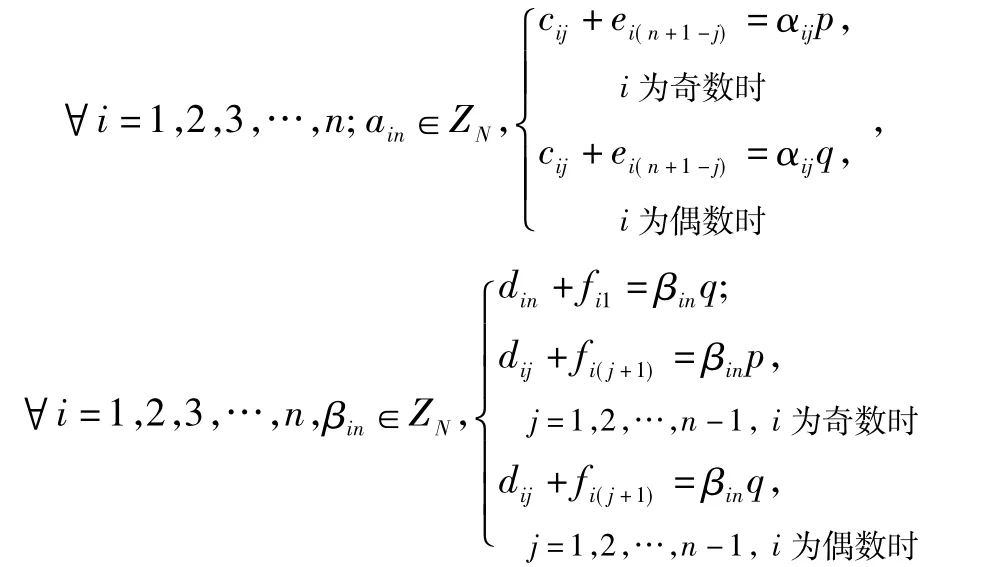
為使該加密算法的解密正確,要求矩陣C、D、E、F是模N可逆的,矩陣D和F模N的逆矩陣分別記作D-1和 F-1,計算如下。
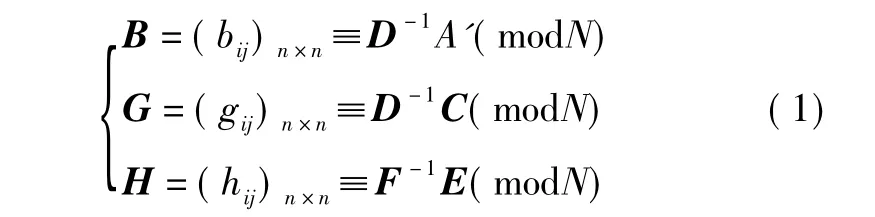
則矩陣B、G、H 和模數 N 是公鑰,私鑰由 D、F、A-1以及 p、q 構成。
2)加密。待加密明文M的長度記為|M|2=ln,將M 分為 n 塊:m1,m2,…,mn,則每塊的長度為|mi|=l。加密明文M,發送者隨機選取2n個整數 r1,r2,…,rn,s1,s2,…,sn∈Zn,計算發送者密文為
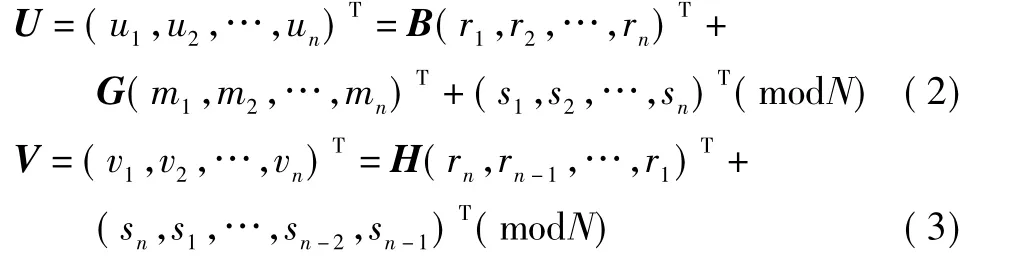
則密文為二元組(U,V)。
3)解密。收到密文對(U,V)后,接收者按下列步驟獲取明文M
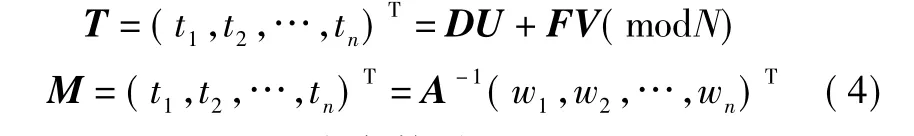
4)參數選取。可以取l=450,設置|aij|2=59。在參數選取過程中A是可逆的,一般A-1中的元素是有理數,這些數很難在計算機中進行有效的表示。因為矩陣A是模N可逆的當且僅當gcd(|A|,N)=1,因此,對于較小的矩陣的維數n和較大的RSA數N=pq,一個隨機選取的n階方陣總是模N可逆的。
3 密鑰分配
對于一些重要的電子公文加密解密過程通常要求由兩人或多人同時參與才能生效,這時就需要將秘密分給多人掌管,并且必須有一定人數的掌管秘密的人同時到場才能恢復這一秘密。在電子公文加密解密中,我們采用Shamir門限秘密分割方案。
Shamir門限方案可按如下的一般方式構造。設GF(q)是一有限域,其中q是一大素數,滿足q≥n+1,秘密s是在GF(q){0}上均勻選取的一個隨機數,表示為 s∈GF(q){0}。k -1 個系數 a0,a1,…,ak-1的選取滿足 ai∈RGF(q){0}(i=1,2,…,k -1)。在 GF(q)上構造一個k-1次多項式
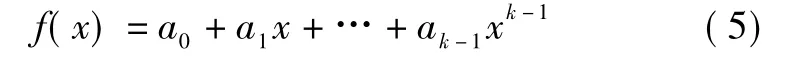
設n個參與者為 p1,p1,…,pn,記 pi分配到的子密鑰為f(i)。如果任意 k個參與者 Pi1,…,Pik,(1≤i1<i2<… <ik≤n)要想得到秘密 s,利用(il,f(il)|l=1,2,…,k)構造線性方程組
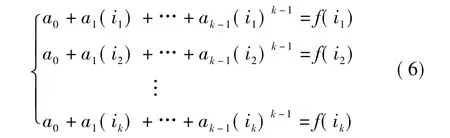
因為il(1≤l≤k)均不相同,所以可由Lagrange插值公式構造多項式
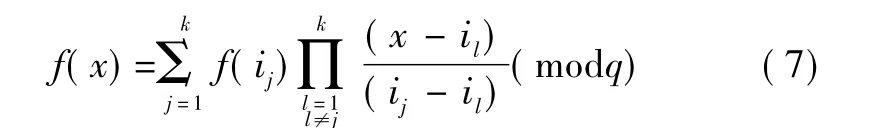
從而可得秘密s=f(0)。
然而,參與者僅需知道f(x)的常數項f(0)而無需知道整個多項式f(x),所以僅根據式(8)就可求出s
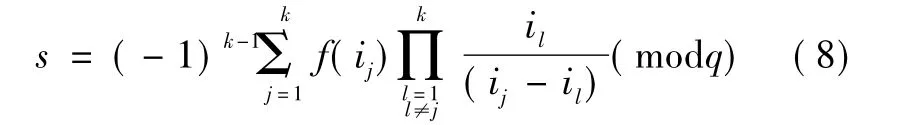
如果k-1個參與者要想獲得秘密s,可構造出由k-1個方程構成的線性方程組,其中有k個未知量。
對GF(q)中的任一值s0,可設f(0)=s0,由此可得第k個方程,并由Lagrange插值公式得出f(x)。因此,對每一s0∈GF(q)都有一個唯一的多項式滿足式(8),所以已知k-1個子密鑰得不到關于秘密s的任何信息,因此這個方案是完善的。
4 性能分析
在本文提出基于矩陣的加密方法中,公鑰由3個n階方陣B、G、H以及模數N構成。因此,公鑰長度大約是(3n2+1)倍的 N 的長度;私鑰包括 D,F,A-1,p,q,因此公鑰和私鑰長度分別可以通過(3n2+1)×1024和2n2×1024+n2×512+2×512來估計。
本文提出的方法和RSA方法都要求生成兩個強素數[13],密鑰生成算法的計算量基本相同。因RSA算法是一個陷門單向置換,其密文擴展為1:1,所以RSA的密文擴展比基于矩陣的密碼算法小。本文方法需要隨機選取幾個模N可逆的矩陣,而RSA方法則需要選取一個加密指數e,根據對密鑰長度的估計,本文方法的密鑰長度要比RSA的大,但基于矩陣的密碼算法總的加解密計算復雜度比RSA方法小。雖然RSA算法可以通過使用中國剩余定理來提高其解密速度,但卻無法做到使其加解密算法的計算復雜度都是二次的,本文加解密算法的計算復雜度都是二次的。RSA方法基于整數分解,而本文方法不是直接基于整數分解,因此,如果整數分解問題被有效地解決了,則RSA算法不一定是安全的,而基于矩陣的密碼算法仍可以使用,可以看出本文提出的方法優于RSA方法。
5 結論
電子公文傳輸系統作為一種安全、高效、高技術的電子政務系統,以其獨特的數字化傳輸技術進行公文的瞬間傳輸,從而徹底改變了延續多年的傳統公文傳遞方式,促進了政府電子政務和企業信息化的快速發展。但是,電子公文是通過網絡傳送的,其傳送和接收是在高度自由的網絡環境中進行的,則必定會存在一定的安全隱患。本文給出了一種基于矩陣的電子公文加密算法,并介紹了電子公文加密中的Shamir門限秘密分割方案,該電子公文安全性方案能大力推動電子政務和企業信息化廣泛和深入的運作。
[1] 張大陸,時慧.電子公文中數字簽名的設計與實現[J].計算機應用研究,2001,18(6):78-80.
[2] 官盱玲.電子公文應用的不安全因素及對策[J].江西行政學院學報,2004(4):84-87.
[3] 謝冬青,冷劍.PKI原理與技術[M].北京:清華大學出版社,2004.
[4] PENG S H,HA K C,KIM J H,et al.New public key cryptosystem using finite non abelian groups[C]//Crypto LNCS 2139.Berlin:Springer-Verlag,2001:470-485.
[5] PENG S H,KWON D,HA K C,et al.Improved public key cryptosystem using finite non abelian groups[DB/OL].IACR Eprint-Server,Report 2001/066,http://eprint.iacr.org/2001/066.
[6] YAMAMURA A.Public-key cryptosystems using the modular group[C]//PKC’1998,LNCS 1431,Berlin:Springer,1998:203-216.
[7] FELLOWS M R,KOBLITZ N.Combinatorial cryptosystems galore[M].Contemparary Mathematics.1994:51-61.
[8] GRANT D,KRASTEV K,LIEMAN D,et al.A public key cryptosystem based on sparse polynomials[C]//Proceedings of an International Conference on Coding Theory,Cryptography and Related Areas,2000:114-121.
[9] YAMAMURA A.A functional cryptosystem using a group action[C]//ACISP’1999,LNCS 1587,Berlin:Springer,1999:314-325.
[10] WANG Baocang,HU Yupu.Public key cryptosystem based on two cryptographic assumptions[J].IEE Proceedings of Communications,2005,152(6):861-865.
[11] WANG Baocang,HU Yupu.Diophantine approximation attack on a fast public key cryptosystem[C]//The 2nd Information Security Practice and Experience Conference,Lecture Notes in Computer Science,Berlin,2006,3903:25-32.
[12] WANG Baocang,HU Yupu.Provably secure public key cryptosystem with double trapdoor decryption mechanism[Z].China Crypt 2006,Jinan:292-296.
[13] 周全,黃繼海.基于多代理的分步簽名方案[J].電光與控制,2006,13(3):105-108.

