學會逆向運用『冪的運算性質』

☉河南省新鄉市第十中學 魏秋菊

冪的運算有四個性質，即同底數冪的乘法性質、冪的乘方性質、積的乘方性質和同底數冪的除法性質.它們是整式乘法的基礎和主要依據，四個運算性質反過來也是成立的，在解題時能正反靈活地運用冪的運算性質，會給解題帶來很大的幫助.

一、同底數冪的乘法公式的逆向運用

逆用同底數冪的乘法法則，可以把一個冪分解成兩個（或兩個以上）同底數冪的積.用式子表示為：am+n=am·an（m，n都是正整數）.其中，拆分所得的（兩個或兩個以上）同底數冪的底數與原來冪的底數相同，指數之和等于原來冪的指數.

例1 若5m=x，5n=y，則5m+n+3=_________.

分析：注意到已知式與未知式之間的底數是相同的，而指數存在著和的關系，于是，逆用法則進行計算.

解 ：5m+n+3=5m·5n·53=125xy.

二、冪的乘方運算性質的逆向運用

例2 若a=2555，b=3444，c=5333，d=6222，試比較a、b、c的大小.

分析：只要將這幾個數化為同指數或同底數進行比較即可，而各個指數均是111的倍數.

解：a=2555=（25）111=32111；

b=3444=（34）111=81111；

c=5333=（53）111=125111；

d=6222=（62）111=36111.因為32＜36＜81＜125，所以a＜d＜b＜c.

三、積的乘方運算性質的逆向運用

積的乘方性質反過來用式子表示為：an·bn=（ab）n（n是正整數）.要準確把握式子的特點，具備能轉化為相同指數的冪的積的式子能應用這一法則，如.靈活地正、反使用本法則可以簡化計算.

例3 計算（-0.125）2005·82007.

分析：當底數間互為倒數時，通常逆用“積的乘方的運算性質”，靈活整合，使得它們的指數相同，使指數都化為2005，這樣就會使運算過程變得簡便，也會使運算結果變得較為簡單.

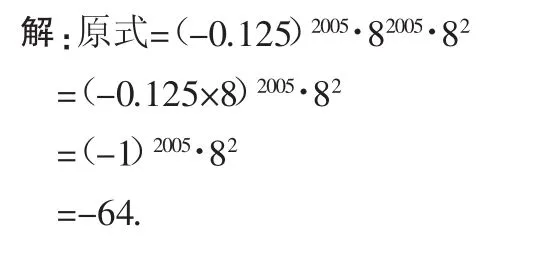
四、同底數冪的除法公式的逆向運用

逆用同底數冪的除法法則，可以把一個冪分解成兩個（或兩個以上）同底數冪的商.用式子表示為：am－n=am÷an（m，n都是正整數）.其中，拆分所得的（兩個或兩個以上）同底數冪的底數與原來冪的底數相同，指數之差等于原來冪的指數.

例4 已知am=9，an=27，求a3m－2n的值.

分析：將指數相減恢復為冪的除法，將指數相乘恢復為冪的乘方.

解：a3m－2n=a3m÷a2n=（am）3÷（an）2=93÷272=36÷36=1.

五、冪的運算性質綜合運用

例5 已知ax=2，ay=5，求a3x-2y的值.

分析：該題可先將同底數冪除法性質反過來運用后得到a3x-2y=a3x÷a2y，這時再將冪的乘方性質逆用一次，得到a3x-2y=a3x÷a2y=（ax）3÷（ay）2，再代入已知條件就可求出所求代數式的值.

例6 若整數N=2m×58是一個11位數，試探求m的所有可能取值.

分析：用一個具體的數字代入顯然是不可取的，應把58設法轉化為108即可.

解：N=2m×58=2m－8×2m×58=2m－8×2×（）

58=2m－8×108，要使整數2m－8×108是一個11位數，只要使2m－8是一個三位數即可，而27，28，29都是三位數，所以m-8的值為7，8，9.所以m的值為15，16，17.

點評：本題靈活運用了積的乘方的逆向運用及同底數冪的乘法的逆向運用，使題目化繁為簡，化難為易，收到事半功倍的效果.