追問引渡 演繹精彩

☉山東省濱州市北鎮中學初中部 邢成云

追問引渡 演繹精彩

☉山東省濱州市北鎮中學初中部 邢成云

提問是課堂教學中不可或缺的交流手段，是開啟學生心智的鑰匙，是引起思考的策動力.陶行知先生云：“發明千千萬，起點是一問．智者問得巧，愚者問得笨．”已經形象地道出了問的重要性.“問得巧”能使得師生思維產生“同頻共振”，增進師生間的信息與情感交流，從而有效驅動學生積極參與.而適時適地、一語深中肯綮地追問（即追根究底地問，是課堂教學中普遍運用的一種方式，它是針對某一內容或某一問題，為了使學生弄懂弄通，在已提出問題、學生也有了一定的理解之后，再次補充或深化的“二度提問”），能有效擴充學生的思維張力，培養學生思維的深刻性品質，收獲生成的碩果.

下面是筆者教學實踐中思考過的一些案例，書來與眾同仁探討.

一、追問——由淺入深

一個問題解決的同時，往往會潛伏著新的問題的出現，若就此打住，學生的思維就會止步，此時若洞察時勢，來一個追問，或許就能激活學生的思維因子，如此，才能撥動心靈的琴弦，啟迪智慧的火花，由淺薄引向深入，會收獲意想不到的效果.

案例 1：學完完全平方公式后，化簡：（n+1）2-n2，學生幾乎都能依據完全平方公式得到正確答案2n+1，若就此作罷，也算完成了本節基本的學習任務.若適時追問，可收獲意外的驚喜.

追問：“若將（n+1）2-n2=2n+1左右交換過來看，你有什么發現？”

學生：2n+1=（n+1）2-n2，多么美妙的結果，當 n 為整數時，這個式子可表示：一個奇數能表示為兩個數平方的差，進一步可能還發現：兩個連續自然數的和可以寫成這兩個數的平方差.

可見一個追問，把一個機械的套公式計算升華為“初等數論”中的問題，帶有數學鑒賞的韻味.

若繼續追問：“這個化簡還有其他方法嗎？”

估計有部分學生能想到逆用平方差公式，即（n+1）2-n2=［（n+1）+n］［（n+1）-n］=2n+1.

若這樣的話，又把學生引向了逆向思維的境界，同時為后續的“因式分解”作出了鋪墊，一箭雙雕.

綜上，在面對一個淺層的問題時，不妨運用教學機智來一個追問，將學生由淺嘗輒止引向“求其甚解”，使學生的思維登臨高處，從而深化學生的認知.

二、追問——指點迷津

英國心理學家貝恩布里說過：“差錯人皆有之，而作為教師，對學生的錯誤不加以利用則是不能原諒的.”初學新知，出現認知偏差在所難免，若一味圍追堵截學生的錯誤認識，往往適得其反，此時不妨沉下心來，把錯誤為己所用，通過追問，引發學生的再度思考，讓學生在自我肯定與否定中，走出迷茫，走向澄明，勝過老師的千言警示.

案例2：學習實數后對“”的認識.

一種觀點（絕大多數人支持）：它是分數；另一種觀點（少數人支持）：它是無理數.

顯然認知對立出現了，孰是孰非，一時難分難解.至此，筆者追問（持分數觀點的）：

師（追問）：π是個什么數？

生：是個無理數.

師（追問）：無理數是如何定義的？

生：無限不循環小數.

師（追問）：一個無限不循環小數除以2后，數的位數怎樣？是否循環？

生：還是無限位，仍然不會循環.

師：那不就自明了嗎？

生（將信將疑）：原來是這樣.

師（繼續）：看來還沒真正領會，那請繼續思考分數是怎么定義的.

生：（一時語塞，其他同學也說不來）

師：那請同學們拿出《現代漢語詞典》查一下，看是如何解釋的？

生（紛紛動手查閱）：把一個單位分成若干等份，表示其中的一份或幾份的數叫做分數.如等.

師：請同學們看這一定義，很明顯，分數的分子分母應該是一個什么數？

生：整數.噢，明白了.

說完后如夢方醒，疑竇頓開：若是分數的話，不但有分數線，分數線上、下兩部分都是整數才行.

這樣，步步為營地追問，把矛盾推向前臺，使學生在接受回答的同時，自行完成了無理數、分數的再次建構，化解了偏頗認知，有迷途知返之效！

案例3：如何構建二次函數模型求最大值？

師：已知周長為60的長方形，什么時候面積最大？最大面積多少？

生（脫口而出）：是正方形時面積最大，最大面積為225.

（說明：學生由經驗可知，周長一定時的長方形面積的最大值是S正方形，故而迅速作出回答）

師：若一邊靠墻，其余三邊總長為60米的長方形什么時候面積最大？

生（很多同學根據原有經驗，仍馬上回答）：也是正方形時.

師（追問）：那么最大面積是多少？

生（通過簡單計算）：邊長為60÷3=20，最大面積S=202=400.

師（故弄玄虛）：老師如果能根據題目中的條件，設計出一個面積大于400的長方形，你們信不信？”

生（眾）：不可能.

師：不信，你們看：如圖（圖略），當垂直于墻的這一邊長為12，另一邊長為36時，滿足周長60，但長方形的面積為432，大于400.

生（眾）：唉，怪了！還有更大的？

學生驚詫中……

師（看時機到，追問）：這種情況下，最大面積到底是多少呢？該怎樣求呢？

生（部分醒悟）：噢，知道了，需要建立函數表達式……

至此，師生帶著問題共同踏上探索之旅：設垂直于墻的邊長為 x 米，則矩形的面積 S=x（60-2x）=-2x2+60x=-2（x2-30x）=-2（x2-30x+225）+450=-2（x-15）2+450，所以當 x=15 時，矩形的面積最大且為450.

點評：學生用了想當然的做法，不顧條件地隨意遷移了自己的經驗，實際上這個信息與原有的知識經驗發生了沖突，通過筆者的追問，好似“仙人指路”，在學生腦海中激起了思維的漣漪，從而把知識的甘泉注入到他們的心田，余味悠長，方法將扎根于學生的腦海中.

三、追問——自悟自醒

數學的學習離不開悟，這是真正理解數學的開始.教師面對一個典型錯誤的出現，往往沉不住氣，急于“一棍子打死”，這樣勢必掩蓋了問題出現的根源，也就做不到“對癥下藥”.但若延遲判斷，把“球”再踢給學生，采取追問導引的方法，把學生的錯誤釣出來，擺在桌面上，學生在心悅誠服后，必定會幡然醒悟，有一番長進.

稍思之后提問一名中等生，答：3.

沒加評判，繼續問：9的算術平方根為什么？

該生答：3.

尚未領會.

師：你知道自己錯在何處了嗎？

……

至此澄明，學生如釋重負，臉上露出笑容.

說明：癥結出在文字與符號的相互干擾上.

四、追問——探明緣由

有很多問題我們可能知其然而不知其所以然，或者利用合情推理得到了猜想，此時學生的思維處于感性的高度，若沒有“為什么”的追問引渡，學生只能在知識海洋的岸邊徘徊，并容易給學生以誤導，犯下想當然的錯誤，若在此探本溯源，適時追問，就可能把學生由感知推向理性，在說理中練就自己的理性精神，使得合情推理與邏輯推理和聲共振，奏出美妙的樂章.

案例5：三角形內角和的教學.

教材上給定的思路是先折紙再說明內角和的度數，這實際上是一種自欺欺人的做法，因為這一結論學生在小學就已經知道了，再故弄玄虛，佯裝不知還有什么意義？鑒于此，還不如直接發問：“同學們知道三角形的內角和是多少嗎？”估計稍有點小學基礎的學生就能作答：“180度.”此時追問：“你能說明這個結論嗎？”估計學生可能一時無語，此刻倒恰好能激起學生的探究欲，然后再引導學生展開探究，既自然順暢，又不失內驅力，學生會在動腦活動中獲得思維的發展，而不是教材中簡單的動手活動.

新課程標準擺正了合情推理的地位，但并不是不要邏輯推理，若我們的認識僅停留在直覺猜測等似真水平上，那我們的思維只能在低空盤旋，不能沖入云霄，當然也就沒有“會當凌絕頂，一覽眾山小”的美妙感覺.若在似真處通過究其緣由式的追問，就能把學生的思維從感性引向理性，在和諧中發展學生的數學素養.

五、追問——引領思維

朱熹言：“讀書無疑者須先教有疑，有疑者卻要無疑，到這里方是長進.”學習如果總是在一種“平衡”與“自足”的狀態下進行，是難以產生沖動與激情的.有時候學生沒有問題是最大的問題，是不求甚解的隱形凸顯，為此，在學習過程中，教師要不失時機地選擇學生學習過程中看似尋常處、無疑處（學生提不出問題，但不慎即無意滑過處）設置問題，挑開學生認識上的“疑點”、“盲點”等，打破平衡，在風平浪靜中布隱患，人為制造認知沖突，掀起思維的波瀾，促使學生醒悟、警覺，實現無疑到有疑，有疑到無疑的轉化，追問的目的是探明學生的思維狀態，對學生解決問題的思維策略進行必要的引領，以防不經意間的滑過，實現平淡向深入的轉化.不然，師生之間的問答就容易變成知識結論的簡單傳遞，無益于學生思維方式的改善.

在學習韋達定理的使用時，學生常常顧此失彼.

案例6：若關于x的一元二次方程x2-mx+2m-1=0的兩個實數根分別是x1、x2，且x12+x22=7，試求m的值.

大部分學生不管三七二十一，把x1+x2=m，x1x2=2m-1代入x12+x22=7（可變為（x1+x2）2－2x1x2=7）中，得 m2－2（2m－1）=7，整理得m2－4m－5=0，解之得 m1=5，m2=－1，大功告成！

實際上，當m=5時，原方程沒有實數根．可見學生的解答出了問題，實際證明，老師就是喊破嗓子明令糾正，學生的問題該怎么錯就怎么錯，此時不妨用追問的方式發問：“能把它們對應的方程的根求出來嗎？”學生自然就能在求根的過程中發現自己的淺薄，原來m取5是行不通的．至此韋達定理的使用條件就不言自明了.否則的話，韋達定理的使用條件很易被漠視，而輕輕從思維區域“滑過”，成為后來的“頑癥”.這樣，督促學生自打自招，自行糾偏，印象勢必深刻、記憶自然久遠，其認識也會在切身感受中得以提升.

六、追問——廣開思路

由于學生的個性差異，思考問題的方式、解決問題的方法等不盡相同，在一個問題暫時性獲解后，可通過追問，引發學生的深度思考，催生奇思妙想，將問題的求解思路拓寬，把學生的思維由狹隘的過道引向“開闊地帶”，會對學生思維品質的養成大有裨益.

案例7：如何畫一條直線把如圖1的平行四邊形面積二等分？

一般學生能獲得如下方法：（1）連對角線所在的直線（圖2、圖 3）；（2）過一組對邊的中點的直線（圖 4、圖 5）.

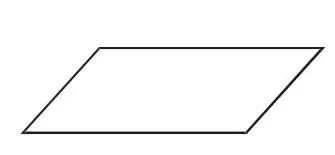
圖1

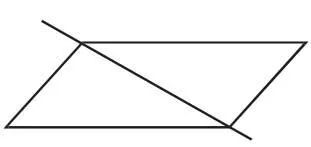
圖2

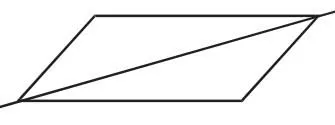
圖3

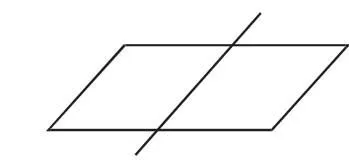
圖4

圖5

問題的獲解往往會帶來學生心理的閉鎖，不想再探索下去.這是一種常態心理，若老師無視這種心理，就此終結，學生就錯失了一次廣開思路的機會，老師不妨來一個追問：還有沒有其他的方法？

實際上，只要通過平行四邊形對角線的中點的直線均可.

若發現有阻力，可繼續追問：若把剛才發現的圖2～圖5的4條直線畫在同一個圖形上，你會發現什么？

學生立即會發現4條直線交于一點，這一點就是對角線的交點.至此，學生會受到啟發，得到猜想：只要過對角線的交點就行.

為了說明方法的可行性，追問：你能證明這一猜想嗎？如此，學生的思維從感性到理性，層層深入，視野跟隨追問不斷開闊.

試想，沒有老師的追問，學生思維可能徘徊不前，可能會留下“入寶山而空返”的遺憾.若通過順勢入理的追問，就能有效喚起學生的潛能，打破學生的惰性心理，突破淺嘗輒止的自我滿足，收獲別樣的精彩.

七、追問——提升規律

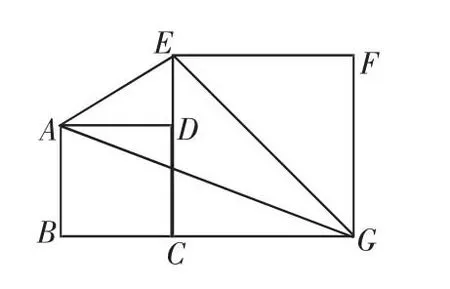
圖6

時下，課堂的開放意識在增強，而開放、真實的課堂將孕育出更多的生成資源，會出現種種的“想不到”，而這些“想不到”中蘊涵著大量有價值的教學資源.由于它是動態的，常常在瞬間流逝，因此需要教師有敏銳的洞察力，及時地捕捉、利用這些資源，適時地實施追問，生成新的教學進程，有意識地把學生的開放的發散思考引向聚合的方向，進而獲得新發現，提煉出展現一般規律的東西.

案例8：《中學數學教學參考》2007年第6期（初中）刊登了《一堂節外生枝的數學課——由一道習題引發的思考》一文，文中列舉了對下面這道習題的七種不同解法.

“如圖6，四邊形ABCD和EFGC是兩個邊長分別為a、b的正方形，用a、b 表示△AGE 的面積.”

文中給出的七種不同解法確實體現了學生的探索精神和創新能力.但作者對這一問題的整體處理尚有欠缺，需進一步完善，在學生給出多種解法后，可設如下追問：

（1）這七種方法有什么共同點嗎？都運用了一種什么思想方法？（都是運用轉化思想將不規則的圖形轉化為規則圖形求解）

（2）本題有沒有更加簡捷的解法？（學生連接AC，得到了∠ACB＝∠EGB＝45°，就有 AC//EG，有了平行線，就有了等積關系，那么△AEG的面積與誰的面積相等？）

（3）變式：如圖 6，點 B、C、G 共線，四邊形 ABCD 和 EFGC是兩個邊長分別為a、2的正方形，試確定△AGE的面積.

這里設計的追問（1）能使學生對數學思想方法的領悟再一次得到升華；追問（2）及時捕捉學生的思想火花，提出最優化解法，有點石成金之效；追問（3）是對本題結果的延伸和拓展.通過這樣內涵豐富的追問，無疑增大了例題的跨度，有利于優化學生的思維，培養學生的創造性．

總之，在學生的思維需要提升時，實施追問，能擴大戰果，便于有效落實“以學定教”的理念，教師的主導作用才會得以“真情綻放”.追問如同引渡的纖繩，能將學生導入智慧的港灣，演繹出精彩的課堂妙段.由于追問往往是不可預設的，因此追問更需要教學機智的支持.正所謂“問在關鍵處，追在當追時”.