巧用數形結合思想的解題探究

☉浙江省三門縣城關中學 牟雪珍

巧用數形結合思想的解題探究

☉浙江省三門縣城關中學 牟雪珍

數形結合思想在新課程背景下，有其廣闊的應用空間.數與形是數學中兩個最基本的研究對象，每一個形都蘊涵著一定的數量關系，而數又常常可以通過圖形做出直觀的描述和反映.“數無形少直觀，形無數難入微”，數形結合就是把抽象的數量關系和直觀的幾何圖形有機地結合起來.這主要包括兩方面的內容：一是“以形助數”，即數量關系借助于圖形及其性質使之直觀化、形象化，從而獲得解題方法；二是“用數解形”，即將幾何圖形的問題經過數量化描述，借助代數計算獲得解題方法.

數形結合 以形助數 用數解形

數形結合思想在新課程背景下，有其廣闊的應用空間.“數”與“形”是數學中兩個最基本的研究對象，每一個“形”中，即每一個幾何圖形中都蘊含著一定的數量關系，而“數”中又常常可以通過幾何圖形做出直觀的描述和反映.“數無形少直觀，形無數難入微”，數形結合就是把抽象的數量關系和直觀的幾何圖形有機地結合起來.就初中數學而言，數軸建立起實數與數軸上點之間的一一對應關系，使得一元代數式與一元方程、不等式有了直觀的幾何意義；平面直角坐標系建立起有序實數對與平面上的點之間的一一對應的關系，使任何一個二元方程或不等式都與平面曲線或平面區域相對應，函數及其圖像詮釋了這種對應關系.另外線段的長度、平面圖形的面積、角的大小以三角函數度量等又從另一角度勾勒了數與形的有機結合.在數與形轉換的理論基礎上自然地產生了數形結合的解題策略：一是“以形助數”，即數量關系借助于圖形及其性質使之直觀化、形象化，從而獲得解題方法；二是“用數解形”，即將幾何圖形的問題經過數量化描述，借助代數計算獲得解題方法.

一、以形助數

“以形助數”，即將代數問題轉化成幾何圖形問題，由圖形性質的啟示抓住問題的本質，以達到解決問題的目的，從而提高分析問題、解決問題的能力.

1.利用數軸將代數問題轉化成幾何圖形問題

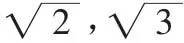
例1 解不等式|x－3|－|x+5|＞2.

分析：題中抽象的數字－5，3用數軸上的點A，B來表示，|x－3|、|x+5|分別表示點X到點B、A的距離.設有一點X1，使X1B－X1A=2，由圖1可知X1表示數－2，而|x－3|－|x+5|＞2表示X1B－X1A＞2，則X在X1左側，所以原不等式的解集為x＜－2.

此類題利用絕對值在數軸上的幾何意義，利用數形結合思想，省去了分段討論的過程，達到以簡馭繁的目的.

2.利用函數圖像將代數問題轉化成幾何問題

利用函數圖像求解方程及不等式，我們首先應該掌握函數圖像（如y=kx，y=k/x，y=kx+b，y=ax2+bx+c）的幾何意義，具體到k，b的幾何意義.

例2 若方程x2+（m+2）x+3=0的兩根均比1大，求m的取值范圍.

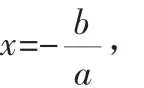
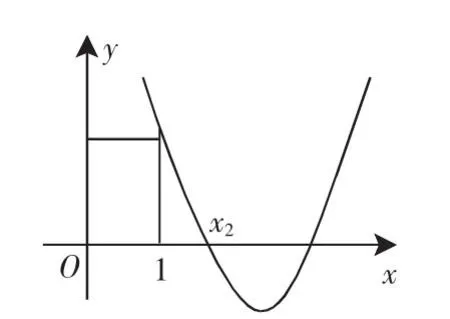
圖2

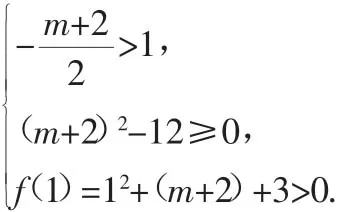
此類題是方程實根分布的圖像解法，利用與已知方程相應的函數圖像來確定實根的分布.用數形結合的方法溝通了方程、不等式、函數和函數圖像之間的聯系，融知識、思想、方法為一體，有利于培養學生的思維能力和綜合運用知識的能力.

3.利用圖形的邊長、面積等將代數問題轉化成幾何問題

利用圖形的面積相等關系，滲透數形結合思想，進一步驗證數學公式.讓學生體會代數和幾何的內在聯系，學會從不同的角度分析問題，培養發散思維.

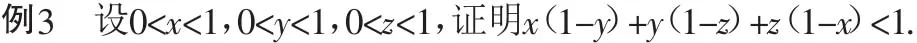
分析：此題直接證明很困難，考慮到左邊是兩個因式乘積之和的形式，而兩因式乘積通常與幾何中面積的度量有關，因此考慮構造幾何圖形來解決.

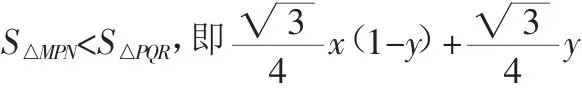
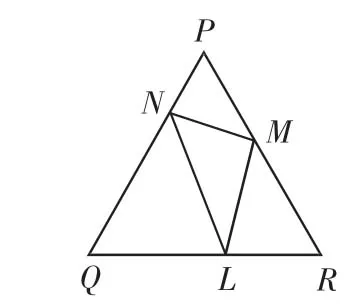
圖3

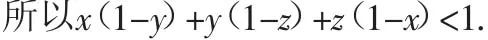
此題是構造等邊三角形來證不等式問題.等邊三角形、等腰三角形、等腰直角三角形、直角三角形等一些特殊圖形，有著特殊的性質，邊和角之間具有一定的量化關系.解題時往往構造這些圖形來解代數問題，使問題變得直觀、形象.

階梯法是一種結構訪談法，有硬階梯法與軟階梯法兩種形式。本文采用硬階梯法，即通過編輯結構式問卷，通過特定的指令，讓受訪者選擇產品屬性再選擇這些屬性所能帶來的結果，并進一步獲得被訪問者使用產品的最終目的，即個人價值觀，形成“由下而上”的階梯。

二、用數解形

“用數解形”，即通過“形”的外表，揭示其內在的數量特征，探討“數”與“形”的本質聯系和規律，將幾何圖形問題經過數量化描述，借助于代數變形獲得解題方法.

1.利用坐標解決平面幾何問題

此類問題要充分利用直角坐標系這個數形結合的重要載體，它使平面幾何的點與坐標系中的一個有序實數對建立一一對應關系.使平面圖形中的點加以量化，準確地反映出來.

例4 如圖4，E是正方形ABCD內一點，且AE=DE，∠DAE=∠ADE=15°.

求證：△CBE是等邊三角形.

證明：以B為原點，BC、BA所在直線為x軸、y軸，建立直角坐標系（如圖），設正方形邊長為a，可知△EBC各頂點坐標為：

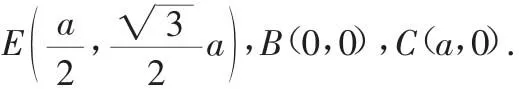
圖4

由兩點間距離可求得EB=EC=a，所以△CBE是等邊三角形.

此題利用直角坐標系，把圖形中的點用準確的坐標來表示.

2.利用方程（組）解決平面幾何問題

例5 如圖5，在△ABC中，D為AB上點，DE∥BC，交AC于點E，設S△ABC=S，S△BDE=S′，求證：S≥4S′.

證明：設DE=x，BC=a，作EF∥AB交BC于F，則BF=x.

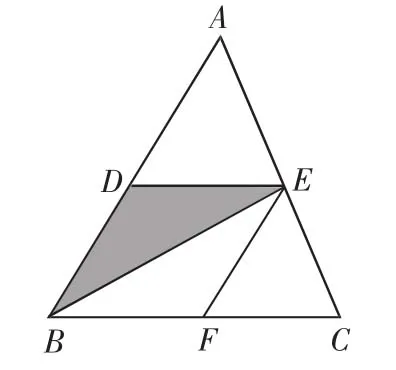
圖5

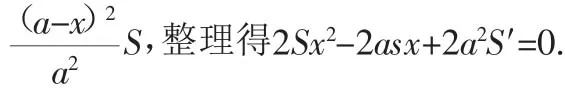
又因為x為實數，所以Δ=4a2S2－16a2SS′≥0，即S≥4S′.

構造二次方程后，可利用違達定理和判別式等進行解題.許多平面幾何問題可以通過設元轉化成方程問題，比如直角三角形中，根據勾股定理和等積法列出方程.近幾年的中考試題中，矩形的翻折問題已成為一個熱點，實質上翻折問題是一個軸對稱問題，根據翻折前后的對應線段和對應角相等，利用方程模式去解決.還可以利用相似圖形的相似比和面積比等列方程，動態幾何問題中的邊長經常用未知數來表示，根據題目中的數量關系利用方程或函數建模來求解.

3.利用函數解決平面幾何問題

例6 △ABC中，∠A=90°，∠C=30°，AB=1，兩個動點P、Q，同時從點A出發，P沿AC運動，Q沿AB，BC運動，結果兩個動點同時到達點C，求點Q在BC上運動時，△APQ的面積的最大值.

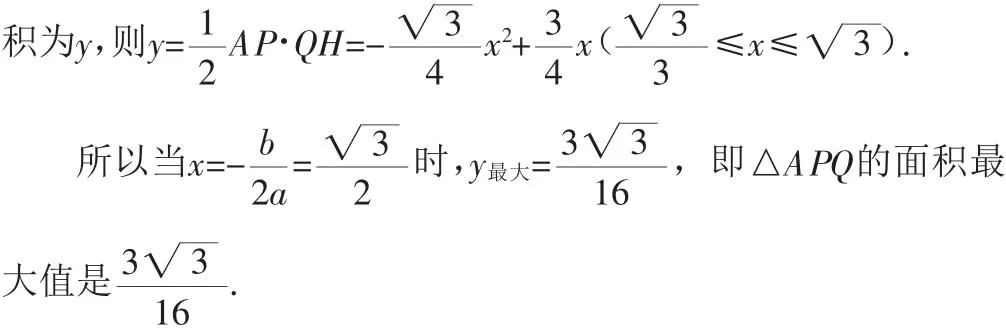
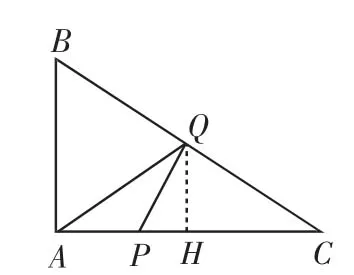
圖6

此題是用代數方法解平面幾何問題，把面積的最值問題轉化成二次函數的最值問題，通過具體的數量關系確定點在圖形中的位置，充分體現了數形結合思想.

“數”與“形”兩者間是互為條件、互相滲透、互相促進的相輔相成的關系，分開是為了對某一方面的本質更深入的研究，結合是對兩者更全面的認識.著名科學家拉格朗日曾經說過：“只要代數同幾何分道揚鑣，它們的進展就緩慢，它們的應用就狹窄，但是當這兩門科學結合為伴侶時，它們就互相吸取新鮮的活力，從那以后，就從快速的步伐走向完善.”

1.吳寶瑩.數無形少直觀，形無數難入微.趙小云，主編.數學教學論文集.

2.盧建狀.證明不等式的數學模型方法.中學數學研究，1995.

3.程時平.拋物線的位置關系符號相關的中考試題淺析.數學教師，1998（3）.

4.葛金良.淺談構圖法在三角函數中的應用.中學教研，1995（11）.