問題驅動課堂教學的理論、模式、實踐探索、反思

☉浙江省余杭中學 程厚軍

一、什么是問題驅動教學

所謂問題驅動教學方法，是基于建構主義教學理論，教師從學生所擁有的樸素的原始觀念出發，設置一系列問題，并對這些問題分析與解決，讓學生在思維參與中體驗到許多的概念、公式、定理、解決問題的思想方法不是“天外來客”，讓學生在問題驅動下理解知識的本質，構建新的知識網絡.它的具體教學基本模式：提出問題——解決問題——反思過程.

二、引入問題驅動式課堂教學的背景分析

“關注學生”是新課程的核心.高中數學課堂教學如何適應新課程改革的要求？如何調動學生的學習積極性？如何引導學生主動學習？如何面向全體學生，讓每個學生在課堂上都動起來？這些就成為我們必須面對和思考的問題.在高中數學課堂中引入“問題驅動”是一種很值得關注和研究的課堂教學模式.

三、引入問題驅動式課堂教學的優點

提倡問題驅動式的課堂教學，是因為它更能促進學生的課堂參與行為和思維.教師提出問題，作為任務驅動學生思考、動手操作.師生共同解決問題的過程也是師生情感交流，融洽課堂氣氛的過程.更重要的是問題驅動式的教學讓學生的課堂學習感覺輕松，只有教師適時的精心設計的點撥，整堂課就在一個個問題的解決中悄然度過，新的知識就在不斷解決問題的過程中被發現、被吸收、被應用.正如蘇霍姆林斯基所說：最好的教育就是讓學生感覺不到在被教育.

四、問題驅動課堂教學的基本模式

1.以“線型問題單元鏈”為主線的問題驅動模式.

線性問題單元驅動模式，采用順向加工的方式，往往從一個簡單的問題開始，有層次地漸近地向目標問題趨近.在這種模式中，教師對問題的設置是關鍵，突出層層驅動，目的是讓學生體驗“數學知識的發生、發展過程”，實現小步驟達到教學目標.整個教學過程由“問題鏈”驅動學生思維逐步深入.（如圖1）

圖1

參見案例4：復數的概念的引入.

2.以“樹型問題單元鏈”為主線的問題驅動模式.

樹型問題驅動模式，采用目標——手段的分析方式，往往根據教學目標先審視并確定要解決的問題（目標），在解決問題的過程中，將目標問題分解為一些子問題或子問題鏈（手段），驅動學生思維，進而找到解決問題的途徑，幫助學生獲得知識，掌握方法，體驗探究過程，理解知識發生、發展過程.

“樹型問題單元鏈”主要有以下幾種形式.

（1）分類并聯，類比聯想.

問題以并聯的形式出現，相對獨立，根據學生的生成情況因勢利導，并列展開，逐個解決，讓幾個問題同時驅動問題解決.（如圖2）

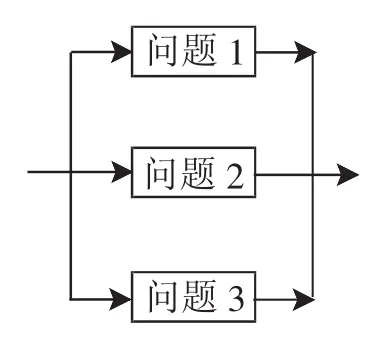
圖2

案例1：二面角定義的形成.

設問1：如何度量異面直線所成角的大小？（轉化為平面角）

設問2：如何度量線面直線所成角的大小？（也是轉化為平面角）

設問3：如何將度量二面角的大小也轉化為平面角的問題呢？

設問4：刻畫二面角的兩條射線應該在什么位置？角的頂點應該在哪里？兩條射線如何放置才能合理刻畫二面角的大小？

最后再給出二面角的定義，讓學生理解定義的合理性.

（2）分解探究，演繹證明.

問題以交叉的形式出現，當要解決一個問題時，不容易得出結論，需要從不同側面、不同角度解決幾個問題，然后在解決幾個問題的基礎上經過推理論證來驅動問題解決.（如圖3）

案例2：余弦定理新課的引入.

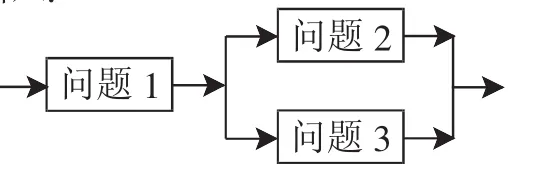
圖3

設問1：1994年，荷蘭弗蘭登塔爾數學教育研究所長Freudenthal在上海華東師大做報告，其中有一個很簡單的問題：甲離學校10千米，乙離甲3千米，問乙離學校多少千米？

設問2：如果甲、乙、學校三點構成直角三角形呢？

設問3：如果甲、乙、學校三點不能構成直角三角形，就變成已知三角形的“兩邊夾一角”，如何求第三邊呢？

用這種方式引入余弦定理，使人倍感親切、自然、合理，數學的魅力也油然而生.

（3）整合分析，歸納概括.

當一個問題比較抽象或涉及范圍較大時，不能直接得出結論.需要從不同的既相對又獨立的幾個問題著手分別研究，從中分析差異，找出個性，歸納類比，從而抽象概括出本質特征.（如圖4）

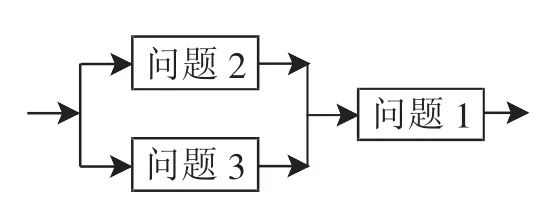
圖4

案例3：“零點存在性定理”的生成.

設問1：如果甲的位置由A變到B，甲過河了嗎？

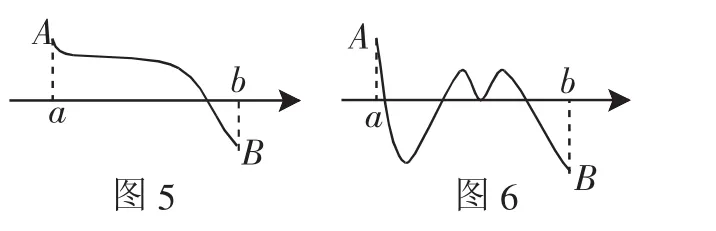
設問2：如果A、B在河的同側，甲過河了嗎？

設問3：如果把河比作直線，滿足什么條件時，甲走的路線一定與直線有交點？

設問4：結合函數的零點的概念，我們可以用怎樣的數學語言來表達上述結論？

五、問題驅動課堂教學實踐探索

1.用問題驅動探索定義的形成，讓學生經歷自我發現的過程.

案例4：以復數的概念為例.建構對復數的理解，應該了解數的擴展過程，復數是如何產生的？我們用以下問題濃縮這個過程，主要展現復數是如何產生的.

設問1：方程x2+1=0有解嗎？為什么？

學生：無解.實數的平方是非負數.負數不能開平方.

設問3：思考一元二次方程x2+2x+3=0的解的情況？

學生：它原先是無解的.

設問4：如果承認-1可以開方，該方程可以求解嗎？

設問6：都可以解了，可是當Δ<0時，我們得到的是什么呢？不妨認為它們是數，這些數有什么特征？

教師：如果承認它是數的話，我們面對的是一類新的數，法國數學家笛卡爾給這些數起名叫虛數，即“虛的數”，與“實數”相對應.我們給一個特征性的記號：用i表示，把a+bi這些新的數稱為復數，其中i稱為虛數單位.

上述設計展現一個新數的創造過程，鼓勵學生的求異思維，在復數概念出現之前，教師通過設計一系列問題，通過問題的分析和解決，有意識的讓學生感受“新數”的存在，并展現存在的合理性，有助于學生對復數概念的接受和理解.

2.用問題驅動化解教學難點.

案例5：設不等式mx2-2x-m+1<0對于滿足-2≤m≤2的m都成立，求x的取值范圍.

教師通常都會給學生介紹下面的解法.

分析：把mx2-2x-m+1看成關于m的一次函數，原問題等價于當-2≤m≤2時，f（m）的圖像為一條線段，對應的兩個端點都應該在m軸下方即可.

解：f（m）=（x2-1）m-2x+1，mx2-2x-m+1<0?f（m）<0.

因為f（m）的圖像是一條直線，所以當m∈［-2，2］時，f（m）<0，當且僅當

這種解法思路巧妙，過程簡潔.但在教學中發現，能真正掌握這一方法的學生很少，說明看似很好的方法直接灌輸給學生，教學的有效性是很低的，學生對解題方法的認識僅停留在欣賞的層面上，沒能真正理解掌握.

本題中，學生理解的難處是x與m的復雜關系，那就從剖析問題的結構、把握x的特點以及它與m的關系入手設計一連串有邏輯關系的問題，為學生鋪設一條通向本質性理解的線路.本題的另一個難點在于把關于x的不等式化歸為關于m的不等式，然后再把關于m的不等式化歸為函數f（m）的圖像在x軸下方.既然兩次化歸是難點，那就通過設置問題幫助學生與原有的知識經驗發生實質性的非人為的聯系，讓學生自己伴隨著漸趨深入的設問來推動問題的解決和數學思想的應用.

設問1：本題涉及哪幾個量？相對于m的變化，你認為x應看成靜止的還是運動的？為什么？

師生探討結果：涉及x和m兩個獨立的變量，相對于m的變化，x應看成靜止的.

設問2：題目的要求是“求x的取值范圍”，看來x又是可以在某一范圍內變化的，你對此怎么理解？x的取值范圍究竟是哪個條件決定的？

師生探討結果：x的值是不確定的，因為滿足條件mx2-2xm+1<0的x值一般不唯一，而是可以在某一范圍內變化的.

設問3：對于每一個確定的m的值，mx2-2x-m+1的值也緊跟著唯一確定了嗎？你為什么這么說？由此可知，mx2-2x-m+1與m是什么關系？

師生探討結果：x和m是相互獨立的兩個變量，當m變化時，mx2-2x-m+1的值也緊跟著唯一確定了，mx2-2x-m+1與m是函數關系.

設問4：記f（m）=mx2-2x-m+1，你能用函數語言重新敘述題目的條件和目標嗎？

師生探討結果：不等式mx2-2x-m+1<0（-2≤m≤2）恒成立問題就等價于函數f（m）=mx2-2x-m+1=（x2-1）m-2x+1（-2≤m≤2）的函數值恒為負數的問題，等價于f（m）max<0（-2≤m≤2）的問題，這是函數思想.

設問5：函數比較抽象，你能從圖像的角度再次敘述原題的條件和目標嗎？

師生探討結果：f（m）=（x2-1）m-2x+1（-2≤m≤2）的函數值恒為負數的問題等價于函數f（m）=（x2-1）m-2x+1（-2≤m≤2）的圖像全在橫軸（m軸）下方的問題，只要函數圖像的最高點在m軸下方即可，這是等價轉化的思想.

設問6：當m∈［-2，2］時，函數y=f（m）的圖像是拋物線嗎？如果不是那應該是什么樣的？

師生探討結果：不是拋物線，是條線段.

設問7：你能再次敘述原題的條件和目標嗎？然后動筆做做看.

師生探討結果：一條線段在橫軸（m軸）下方，當且僅當這條線段的兩個端點都在橫軸（m軸）下方.f（m）=（x2-1）m-2x+1（-2≤m≤2）圖像全在橫軸（m軸）下方的問題，如圖7、圖8、圖9所示，只要f（-2）＜0且f（2）＜0即可.

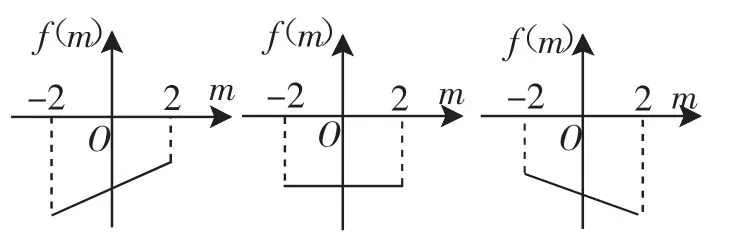
圖7 圖8 圖9

上述系列問題重在引導學生思維的深度參與，讓學生對冰冷的問題進行深入的思考，使學生對問題的理解和方法的領悟建立在自身思維體驗的基礎上，而不是賞析層面.同時，設問基礎上的教師講述和點撥更注重傳授數學思想，引導學生領悟思維本質.

六、問題驅動課堂教學感悟與反思

問題驅動教學改變了教師的教學方式，倡導教師用探尋和追求精神來思考“學生學什么”和“我該怎么教”的問題.就一線教師而言，抽象談論整個學科的本質是困難的，但具體到某一個教學內容來思考它的本質問題——如原初觀念、樸素想法、核心思想、結構方法則是可取的，這種思維方式本身可以引導教師對學科教學的認識向縱深發展.

問題驅動式課堂教學改變了學生的學習方式，充分尊重和發揮了學生的主體地位和作用，增加了學生的主觀能動性和合作精神，促進了他們思維的發展，使學生真正成為學習的主人，而教師要做的是設計出適合學生動手的、能激發他們思維和興趣的問題，通過設計合適的問題驅動學生自己來完成教學任務.

在問題驅動式課堂教學的過程中也存在一些問題.

在實際教學中，往往由于一些主觀和客觀上的原因降低了問題驅動式教學的有效性.很多時候教師提出的問題對學生而言確實是高認知水平的任務，而教學過程中，卻把它降低為低認知水平的任務，主要原因為以下幾點.

1.教師把重點從意義、概念、理解轉移到答案的正確性和完整性方面；

2.教師把任務的問題方面常規化：詳細指明操作程序和步驟，“包辦”學生的思維和推理，以降低任務的復雜的程度；

3.教師設置的問題脫離學生實際，問題的表達欠明確或欠妥帖；

4.教師把問題異化為灌輸知識的載體；

5.任務指向不明，學生不能進入正確的認識空間.

1.楊曉翔.“問題串”的教學設計和實施.中學數學教學參考（上旬），2009，1～2.

2.楊玉東.“本源性數學問題驅動課堂教學”的比較研究.上海：華東師范大學，2004.

3.陳華曲.基于“問題導學”的“反函數”教學設計與心得.中學數學教學參考（上旬），2011，1～2.