深度解讀函數單調性

☉江蘇省如皋市城西中學 章春娟

深度解讀函數單調性

☉江蘇省如皋市城西中學 章春娟

函數是高中數學的核心內容，單調性是函數最重要的性質之一，它反映了函數值的變化規律．縱觀歷年高考，對單調性的考查主要體現在以下四個方面：（1）單調性的定義；（2）單調區間的求解；（3）利用單調性求參數的取值范圍；（4）單調性的應用．下面就這四個方面舉例分析．

一、單調性的定義

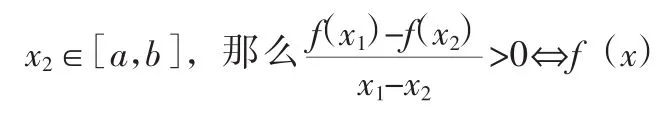
例1若函數y=f（x）在R上單調遞增，且f（m2）＞f（－m），則實數m的取值范圍是（）．

A．（－∞，－1）B．（0，+∞）

C．（－1，0）D．（－∞，－1）∪（0，+∞）解析：由函數單調性的定義可得m2＞－m，解得答案為D．

例2已知f（x）是定義在R上的偶函數，它在［0，+∞）上遞減，那么一定有（ ）．

二、單調區間的求解

求函數的單調區間，除了利用單調性的定義及已知的基本初等函數的單調性外，還可以利用函數的導數法、子集法、圖像法、復合函數的單調性“同增異減”、奇函數在對稱的單調區間內有相同的單調性、偶函數在對稱的單調區間內具有相反的單調性、互為反函數的兩個函數具有相同的單調性這些方法求解．在公共定義域內，增函數f（x）+增函數g（x）是增函數；減函數f（x）+減函數g（x）是減函數；增函數f（x）－減函數g（x）是增函數；減函數f（x）－增函數g（x）是減函數．

例3函數y=log0.7（x2－3x+2）的單調區間為______.

解析：由x2－3x+2＞0，解得函數的定義域為（－∞，1）∪（2，+∞）.據復合函數單調性的同增異減性質得函數y=log0.7（x2－3x+2）的單調遞增區間為（－∞，1），單調遞減區間為（2，+∞）.

點評：本題求解中應先求函數的定義域，單調區間為定義域的子區間.

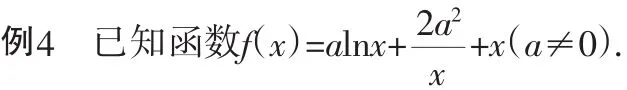
（1）若曲線y=f（x）在點（1，f（1））處的切線與直線x－2y=0垂直，求實數a的值.

（2）討論函數f（x）的單調性.

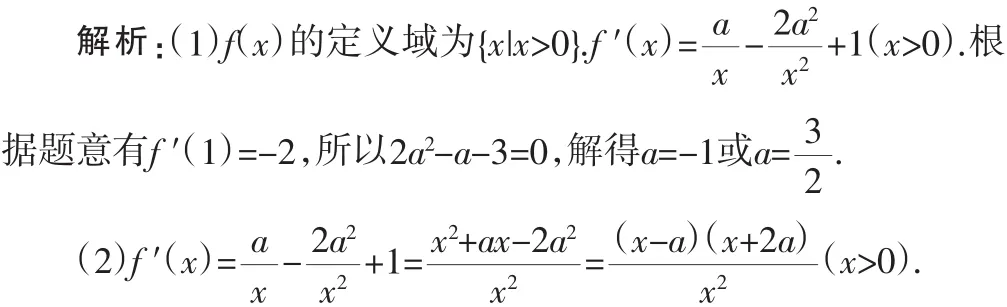
當a＞0時，因為x＞0，由f′（x）＞0得（x－a）（x+2a）＞0，解得x＞a；

由f′（x）＜0得（x－a）（x+2a）＜0，解得0＜x＜a.所以函數f（x）在（a，+∞）上單調遞增，在（0，a）上單調遞減.

當a＜0時，因為x＞0，由f′（x）＞0得（x－a）（x+2a）＞0，解得x＞－2a；由f′（x）＜0得（x－a）（x+2a）＜0，解得0＜x＜－2a.所以函數f（x）在（0，－2a）上單調遞減，在（－2a，+∞）上單調遞增.

點評：導數的引入給函數單調性的研究帶來了很多方便，為函數單調性的判斷提供了程序化的解題思路.實踐經驗告訴我們，含參函數的單調性問題是高考的重點，也是函數研究中最基本最重要的問題，解題中需要對參數的取值范圍進行討論.

三、單調性的應用

單調性有著極其廣泛的應用，在高考中主要體現在利用單調性解不等式、求最值、比較大小.

四、利用單調性求參數的范圍

例7（2012年高考上海）已知函數f（x）=e|x－a|（a為常數）.若

f（x）在區間［1，+∞）上是增函數，則a的取值范圍是______.

由g（x）的圖像知f（x）在區間［1，+∞）上是增函數時，a≤1.

圖1

（1）求函數f（x）的解析式.

（2）若函數f（x）在區間（m，2m+1）上為增函數，求實數m的取值范圍.

解得－1＜m≤0，即m∈（－1，0］時，函數f（x）在（m，2m+1）上為增函數.

點評：在利用區間（m，2m+1）為區間（－1，1）的子區間時，除了m≥－1且2m+1≤1兩個條件限制之外，不可忽視條件2m+1＞m，即必須確保給定區間為非空集合，這一點在解題時極易忽略，容易造成解題錯誤.