基于兩個代理人下的激勵機制設計

汪磊 徐榮

（安徽工程大學管理學院，安徽 蕪湖 241000）

基于兩個代理人下的激勵機制設計

汪磊 徐榮

（安徽工程大學管理學院，安徽 蕪湖 241000）

針對目前研究常采用的“一個委托人和一個代理人”這一假設的局限性，將關于代理人的假設拓展到兩個代理人。通過對兩個代理人的激勵機制進行研究，得出了委托人在引入兩個代理人的情況下能更有效地提高代理人工作努力的水平，從而提高委托人的收益；并且，激勵機制優化的效果取決于代理人面對的外部風險占其業績風險的比率。

委托-代理理論；激勵機制；最優線性合同

自從1973年Ross提出的委托代理的概念[1]，委托-代理關系研究一直是學術界研究的前沿性課題。由于委托-代理關系實際上存在著一種博弈關系，雙方從自己的利益(或者效用)出發參與博弈[2]；而激勵機制的設計是調節委托-代理關系的一個重要工具[3]。從目前的研究現狀來看，大多數研究都是建立單代理人基礎上，對多代理人的情況研究較少。然而，在實際經濟活動中卻存在著一個委托人與多個代理人之間的博弈，近年來多代理人問題[4]成為學界研究的熱點之一。

本文在文獻[2，3，4]的基礎上，針對目前研究常采用的“一個代理人和一個委托人”這一假設的局限性，將委托人的數量拓展到兩個。在研究具有兩個代理人的激勵合同時，個人化信息模型不僅運用個人化信息分析為每個代理人設計的合同，而且運用其他代理人獲得有關結果的信息。當其他人的結果能夠顯示某個代理人行為時，委托人根據該代理人與其他代理人的產量支付給每個代理人。如果其他代理人的結果不會增加信息，那么，他將僅僅依據他自己的結果而被支付。

1 條件假設

假設1委托人P（公司股東或企業所有者）、兩個同質的代理人（經理人員）Ai，i=1，2都是獨立的利益主體，他們的目標都是最大化自己的利益。委托人是風險中性的，代理人是風險規避的[2，3]。

假設2委托人對代理人的努力程度具有非對稱信息（該信息只有代理人自己知道，為私人信息），但可以觀測到兩個代理人的工作業績。根據其業績提供線性合同wAi=α＋βπi＋γπj（即總工資=固定工資+業績提成+代理人j利潤對工資的影響）。委托人的問題是選擇最優的α，β和γ，代理人i決定其工作的努力程度ai。

假設3代理人的產出為πi=ai+θ＋ωi。其中，ai為代理人的努力程度；θ為代理人面對的外生隨機變量（如市場的不確定性）；ωi可以理解為代理人的經營能力。θ和ωi是正態獨立分布的，θ分布服從N（0，σ2θ），ωi分布服從N（0，σ2ω）；進一步，假定隨機變量ω1和ω2相互獨立。

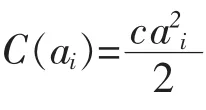
2 委托人及代理人收益表達

委托人收益為公司業績與代理人報酬之差

由于假定委托人是風險中性的，給定wp，其期望效用等于期望收入：

代理人i的收入為代理人所得報酬與其成本之差值

現設代理人i的效用函數具有不變的絕對風險規避特征，即u（wAi）=-exp（-ρwAi）。且兩個代理人的絕對風險規避度均為ρ>0。那么，代理人i的確定性等價收入為：

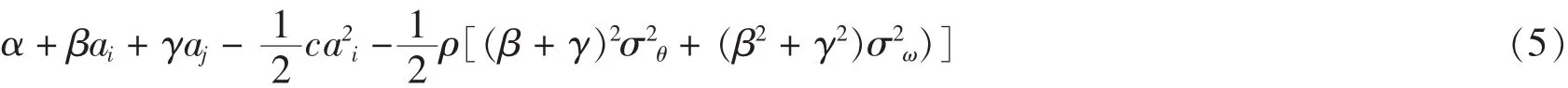
記為fAi。代理人i最大化期望效用Eu=-Ee-ρω等價于最大化上述確定性等價收入式（5）。

3 兩個代理人假設下激勵機制設計

在委托人對代理人的努力程度具有非對稱信息時，委托人所面臨的問題是在考慮代理人利益的情況下，設計適當的線性合同——確定合同中的固定工資、提成比例值和代理人 利潤對工資的影響程度，以誘導代理人努力工作，從而使自己利益的最大化。由于代理人是獨立的利益主體，在委托人給出合同之后，代理人將會考慮到自己的利益，確定最優的努力水平以最大化自己的收益（即激勵相容約束IC）；同時，代理人參與這項工作的最低條件是他所得到的收益不能低于其保留收益（即個人理性約束IR），否則代理人將另尋工作。

該問題的委托代理模型如下所示：

對模型（6）中的（IC）進行一階、二階微分，有

將式（9）代替模型（6）中的（IC）條件中，可得到fA1=fA2=fA，與之等價的模型如下：

由Kuhn-Tucker最優化條件有

解方程組（11）可得：

因為該非線形規劃問題為凸規劃問題，Kuhn-Tucker最優化條件下的α，β，γ為全局最優。

4 結果分析與比較

本文所述模型與一些已有模型進行比較,得表1

表1 一個代理人與兩個代理人情況下各指標對比

從表1給出的一個代理人與兩個代理人情況下各指標對比可以得出：兩個代理人情況下的代理人努力水平和委托人收益要明顯地優于一個代理人的情況。因此，筆者認為：委托人可以通過聘用兩個代理人來提高單個代理人的努力水平，從而達到增加委托人收益的目的。

5 結束語

本文詳細探討了基于兩個代理人的激勵機制設計。首先通過模型分析，得出了引入兩個代理人后的最優的激勵合同。然后對模型中的最優合同的系數進行了討論，最后從與一個代理人情況下最優合同的分析比較中得出“兩個代理人情況下的代理人努力水平和委托人收益要明顯地優于一個代理人的情況”的結論；并且，其優化的效果取決于代理人面對的外部風險占其業績風險比率的大小。

由于實際經濟活動中常常存在兩個或兩個以上代理人,因而基于兩個代理人的激勵機制設計問題研究具有相當的理論和實際意義,能夠得到一些新的結論,并有利于決策的進行。

[1]Ross,S.The Economic Theory of Agncy:The Principal’s Problem[J].American Economic Review，1973，（63）:134-140.

[2]張維迎.博弈論與信息經濟學[M].上海:上海人民出版社，1996：431-463.

[3]Holmstrom,B.and P.Milgrom.Aggregation and Linearity in the Provision of Intertemporal Incentives[J].Econometrica，1987，（55）:303-328.

[4]Al-NajjarNI.Incentivecontractsintwo-sidedmoralhazardswithmultipleagents[J].Journalofeconomictheory,1997,（1）:174-195.

[5]Grossman,S.,and O.Hart.An Analysis of the Principal-Agent Problem[J].Economtrica,1983，（51）:7-45.

[6]Hart,O.Firms,Contracts and Financial Structure[M].Paper Presented at Clarendon Lectures.Oxford:Oxford University Press，1995:65

[7]Holmstrom,B,Moral Hazard and Observability[J].Bll Journal of Economics,1979,（10）:74-91.

DESIGNMENT FOR THE INCENTIVE MECHANISM BASED ON TWO AGENTS

WANG LeiXU Rong
(Management School,Anhui Polytechnic University,Wuhu Anhui 241000)

The paper assume two agents for the Study limitations of a principal and an agent,By studying the two agent's incentive mechanism,discover that the agent can effectively improve the level of work effort and the client's income in the case of the introduction of two agents,and the optimization of the mechanism effects depend on external risks faced by agents to the performance of its risk ratio.

principal-agent theory；Incentive Mechanism；Optimal linear contract.

book=41,ebook=40

F224

：A

：1672-2868（2012）04-0041-04

責任編輯：澍 斌

2012-06-21

安徽省教育廳人文社會科學重點資助項目（項目編號：SK2012A020）

汪磊（1984-），男，安徽蕪湖人。安徽工程大學管理工程學院助教，研究方向：人力資源管理。