改進的主成分分析法在多響應優化中的應用*

張迎冬，何 楨

(天津大學管理與經濟學部，天津 300072)

改進的主成分分析法在多響應優化中的應用*

張迎冬，何 楨

(天津大學管理與經濟學部，天津 300072)

提出了一種改進的主成分分析法，在解決多響應優化問題時考慮到模型的預測能力。主成分分析法是一種常用的多響應優化方法，為了在應用主成分分析法的過程中考慮到模型的預測能力，文章將回歸方程擬合度R2系數結合到主成分分析中。與主成分分析法相比，該方法不僅能利用主成分得分將多個響應轉化為單一響應，還能考慮到不同響應的預測能力。實例表明，用該方法得到的結果可體現出模型預測能力的影響，并且預測能力強的響應得到較大的改進。

質量工程;多響應優化;主成分分析法;預測能力

0 引言

試驗設計旨在通過調整系統中的輸入變量以分析輸入變量與輸出響應之間的關系，并使輸出響應達到最優值。系統中只有一個輸出響應的問題稱為單響應優化問題，此類問題較易解決，通過回歸方法以及一般的優化方法就能實現。然而，在現實的工業生產中會遇到有多個輸出響應的試驗設計問題，該類問題較難解決，這就是所謂的多響應優化問題。多響應優化是質量工程領域面臨的主要問題之一。

多響應優化問題的目的是找到一組合理的輸入變量，同時優化多個響應。但在實際問題中，多個響應變量可能會相互影響，導致多個響應變量不能同時達到最優，因此解決多響應優化問題就轉變為如何找到一組輸入變量，使所有響應變量盡可能的接近其最優值，以達到多個響應整體的最優而不是單個響應的最優。現階段解決多響應優化問題的主要思路是通過降維技術將多響應問題轉化為單響應問題。目前多響應優化方法主要有滿意度函數法、廣義距離法、損失函數法、概率法和主成分分析法等。

主成分分析法是解決多響應優化問題的常用方法之一，但其在應用過程中沒有考慮到各響應回歸方程的預測能力，本文將對加權主成分分析法進行改進，提出一種考慮預測能力的加權主成分分析法，并用該方法對文獻中的實際問題進行分析。

1 主成分分析法

1.1 加權主成分分析法

主成分分析法可將p個相關的原始變量轉化為k(k≤p)個無關的主成分，實現降維的目的。Su和Tong［1］、Antony［2］、鐘曉芳［3］等提出了基于主成分分析的多響應優化方法，利用主成分分析法將p個輸出響應(需對數據進行標準化處理以消除量綱的影響)轉化為k(k≤p)個無關的主成分，并選取特征值大于1的主成分作為最終的優化指標。

Liao［4］指出該方法仍有兩個主要的缺陷:第一，若特征值大于1的主成分大于一個，該問題仍然是一個多響應問題;第二，挑選出的主成分不能解釋原變量的全部方差，造成信息的丟失。Liao［4］選取每個主成分的方差貢獻率作為該主成分的權重，提出了一種基于加權主成分分析的多響應優化方法，該方法以主成分的綜合得分，即加權主成分之和作為多響應績效指標，綜合考慮所有主成分，解決了上述的兩個問題。

用Yj表示第j個響應的標準化信噪比(望大特性)，對Yj進行主成分分析，可將p(假設多響應問題中有p個輸出響應)個響應轉化為k(k≤p)個無關的主成分，即:

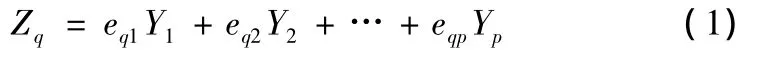
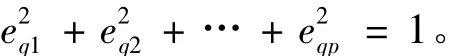
主成分的方差貢獻率為該主成分所解釋的方差占總方差的比例，反映各主成分的信息含量多少，其值為:

其中，Wq為第q個主成分的方差貢獻率，λq為Y的協方差矩陣的第q個特征值。

Liao［4］選取每個主成分的方差貢獻率作為該主成分的權重，計算k個主成分的加權和，得到主成分的綜合得分，將多響應問題完全轉化為單響應問題。定義MPI(Multi-response Performance Index，多響應績效指標)為:

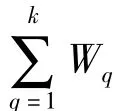
Liao［4］提出的加權主成分分析法完全將多響應問題轉化為單響應優化問題，并解釋了原問題的全部方差。Gauri和 Chakraborty［5］，Shih 和 Tzeng 等［6］進行實證研究，利用加權主成分分析法解決實際工業生產中的多響應問題，得到了理想的結果。

1.2 改進的方法

加權主成分分析法的優勢在于其將復雜的多響應問題轉化為求MPI最大值的單響應問題，同時通過所有主成分加權和的形式解釋了原響應的全部方差。但其仍存在一定不足之處，在計算過程中并沒有考慮到響應回歸方程的擬合度，即模型的預測能力。本文將針對這一問題，對該模型進行改進。

Kim和Lin［7］將預測能力結合到滿意度函數中，并指出回歸方程的擬合度較高的響應對優化結果有較強的影響，因此在各響應回歸方程的擬合度有顯著差別時如若不考慮模型的預測能力將會對優化結果產生不利的影響。預測能力，即擬合度的度量可采用R2，R2－adj，均方誤差等指標，為方便敘述，本文采用最為常用的R2來度量預測能力，其他指標的使用與R2相似。

考慮到信噪比本身的缺陷［8］，本文采用各響應值的均值作為分析數據，進而更好地分析各響應回歸模型的預測能力。在多響應問題中，定義有p個響應變量，共進行m次試驗，以yij表示第i個響應在第j次試驗中的均值。為消除量綱的影響，對各響應均值進行標準化，得到標準化均值，如下:

其中，Yij表示標準化后的均值，μi和σi表示第i個響應的m個值(共進行m次試驗)的平均值與標準差。

可見，ri在(0，1)之間，且r1+r2+… +rp=1。

ri表示第i個響應的預測能力，為了在主成分分析中考慮模型的預測能力，對原模型進行修改，將ri結合到主成分之中，如下所示:

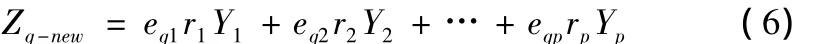
其中，Zq－new表示結合了預測能力的第q個主成分。

在原始的主成分公式中，系數向量eq=(eq1，eq2，…，eqp)'為向量 Y=(Y1，Y2，…，YP)'的方差協方差矩陣的特征向量，特征向量為單位向量，選取特征向量作為系數向量保證了以下兩個條件:

(1)確保該主成分的方差為最大值，且其值等于特征值，用公式表示為:

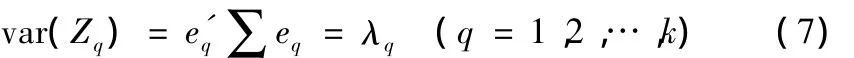
本文給出的主成分公式，如(6)式所示，主成分系數不再是特征向量，但在加權主成分分析中，采用主成分的方差貢獻率作為各主成分的權重，即仍保持各主成分的方差值等于相應的特征值，且綜合考慮全部主成分，能夠解釋原問題的全部方差，不破壞上述條件。

(2)確保各主成分之間相互獨立，用公式表示為:

通過分析可知，改進后的主成分系數向量不是單位向量，不能確保各主成分之間一定相互獨立。但當原問題中各響應間相關性較小時，該方法仍然適用。

Richard和Dean［9］指出，主成分系數向量 eq=(eq1，eq2，…，eqp)'中的每一個分量eqn的大小度量第n個變量對第q個主成分的重要程度。本文將R2系數融入到系數向量中，用ri表征第i個響應預測能力對主成分的影響，并最終影響可控變量組合的選取。

改進后的加權主成分分析法的MPI為:

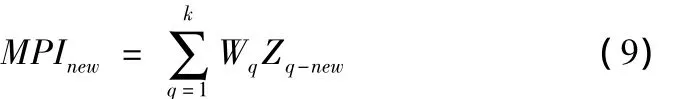
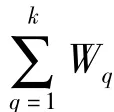
通過(6)式和(9)式可以看出，最后的MPI值可完全轉化為標準化均值的函數，即MPI=f(Y1，Y2，…，Yp)，預測能力的影響也會通過對系數向量的修改而最終轉化到決策過程中，預測能力強的響應將會有較大的系數，優化時也會得到更多的側重性。優化MPI值可獲得最佳的可控變量組合，在考慮預測能力的同時使多響應問題整體效果達到最優。

本文提出的方法在加權主成分分析法的基礎上結合了響應回歸方程的R2系數，考慮了模型的預測能力。該方法存在著一定的局限性，如上所述，結合了R的主成分系數不能保證主成分之間恒為相互獨立，但在原響應之間相關性較小時，該方法依然能發揮其優勢:將多響應問題轉化為單響應問題，解釋原響應的全部方差，并考慮模型的預測能力。

2 應用實例

本文采用文獻［6］中的案例進行分析。該試驗研究金屬惰氣(MIG)電弧焊泡沫板的優化問題，共有兩個響應，顯微硬度和彎曲強度，兩個響應均為望大特性，共受8個因子影響，分別為填充材料(A)、MIG流(B)、焊接速度(C)、MIG氣臨率(D)、工件差距(E)、MIG電弧焊角度(F)、槽角(G)和電極延伸長度(H)。其中只有填充材料(A)取兩水平，其他因子均取三水平，進行田口L18(21*37)試驗設計。試驗設計安排及試驗結果如表1所示。

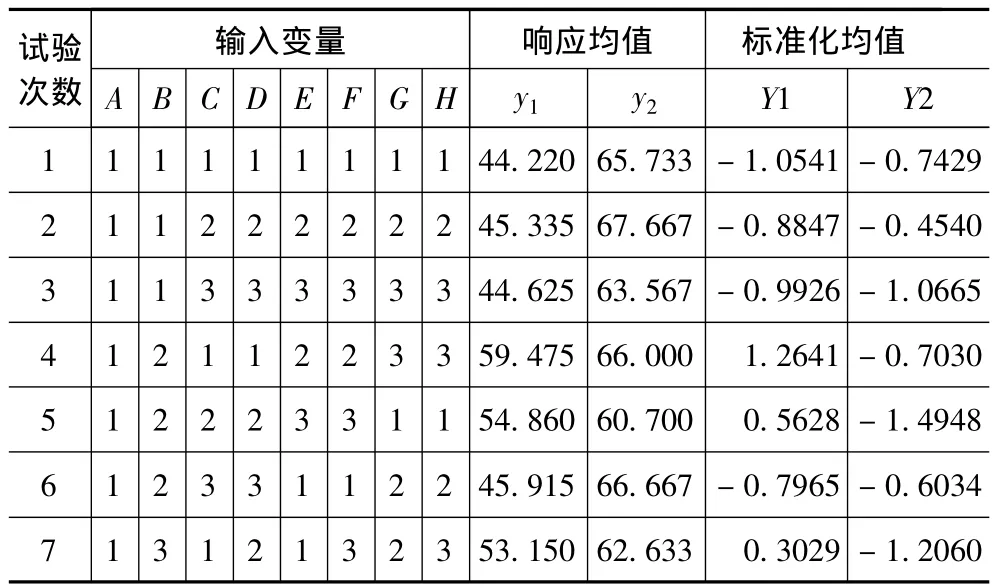
表1 試驗設計及響應均值表

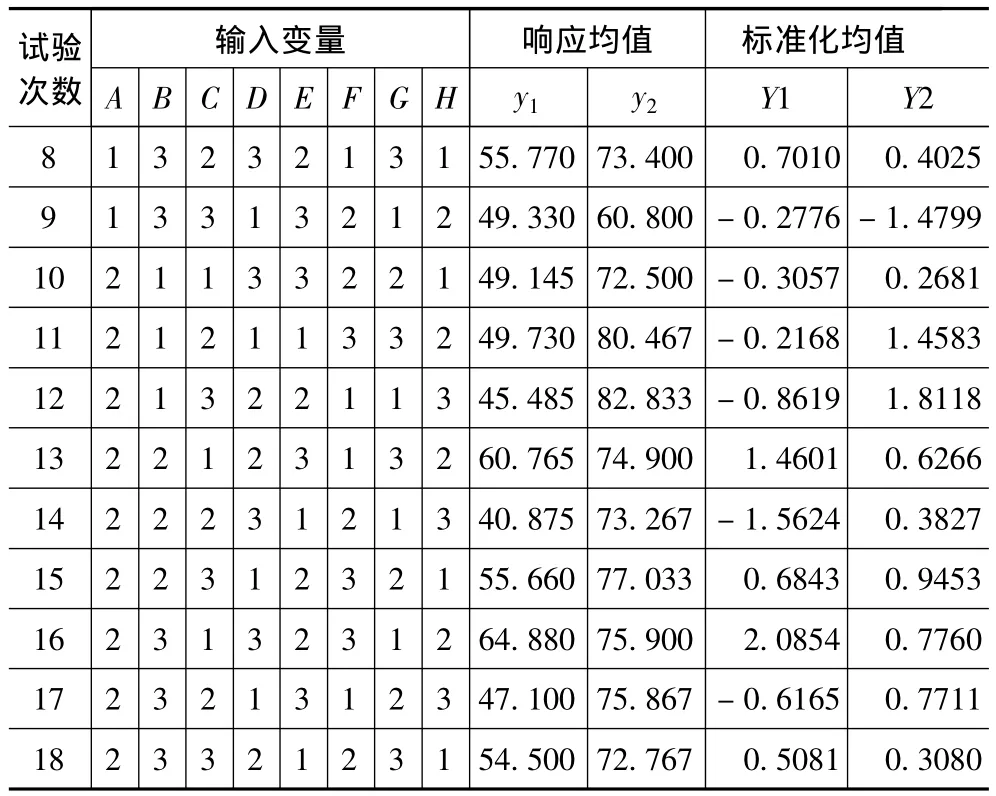
(續表)

各響應的標準化均值均由Minitab軟件得到，利用響應均值可得到兩個響應的回歸模型及R2值，如下所示:

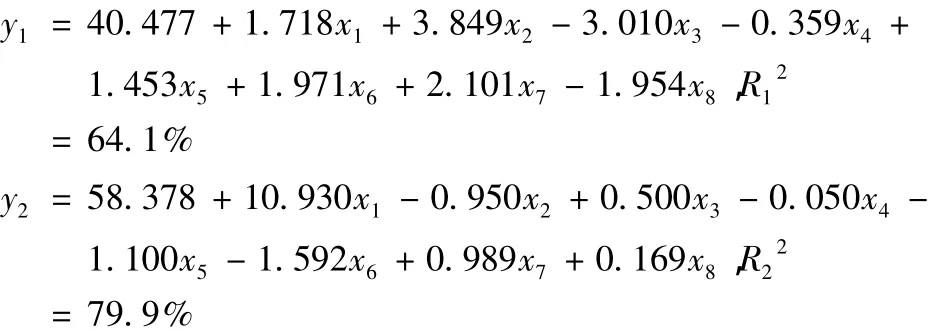
由式(5)得到標準化的預測能力，r1=0.445，r2=0.555。

利用SPSS軟件進行主成分分析，可得到主成分的特征值和特征向量矩陣，如表2所示。

表2 主成分分析表

由式(6)，可得到相應的兩個主成分:

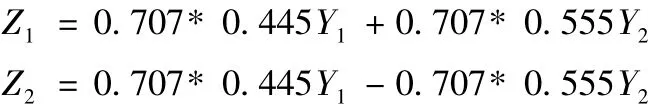
由式(9)，可得到改進后的多響應績效指標MPI:

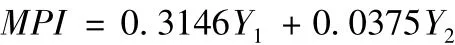
根據上式可計算出每次試驗下的MPI值，如表3所示。

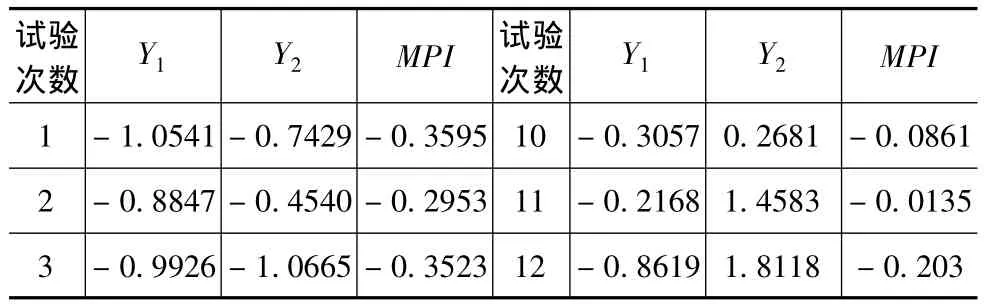
表3 MPI值表

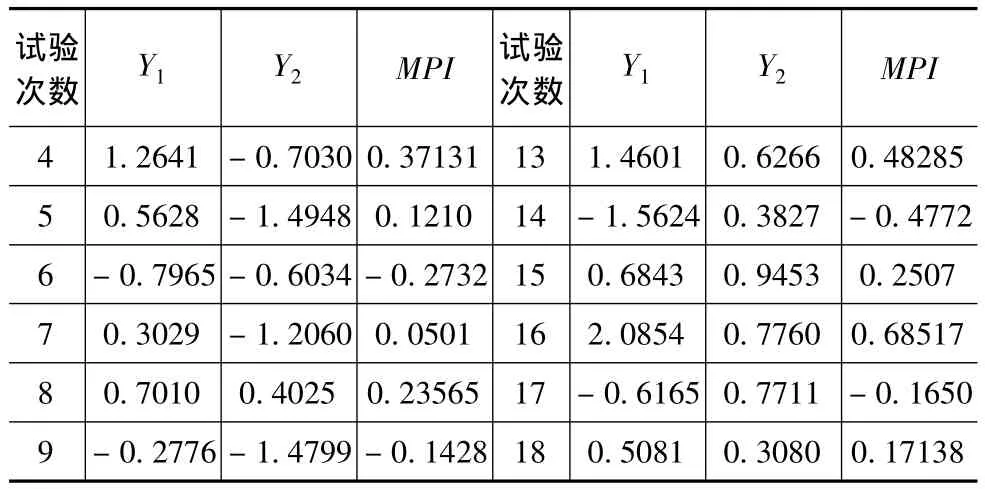
(續表)

通過表3，可計算出各因子的主效應值，如表4所示。

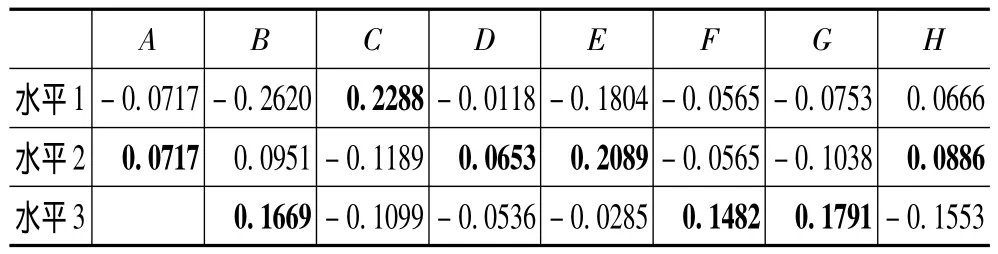
表4 主效應值表

本例中，MPI值越大，質量特性越好，因此使MPI主效應最大的因子水平組合即為該因子的優化結果，由表4可看出，最優因子設置為:A2B3C1D2E2F3G3H2。將最優因子設置帶入到回歸方程中，可得到此時y1=62.946，y2=74.117。

用本文提出的方法所得的結果與文獻［6］中的結果相比較，如表5所示。

表5 優化結果比較表

從上表可以看出，由于考慮了響應的預測能力，本例得到的最優因子設置有所不同，此時得到的y1值比加權主成分分析法得到的y1值小，而y2值變大，因為兩響應同為望大特性，顯然該結果對響應y2有較大的偏重性，較大的優化了y2。這是因為響應y2的預測能力較強(R2系數較大)，改進的主成分分析法突出了預測能力對優化結果的影響。在實際應用過程中，根據響應預測能力的相對重要程度及實驗者的意愿，可對R2系數進行處理，擴大或縮小不同響應間的相對差距，以凸顯各響應預測能力對優化結果的影響。

3 結束語

本文提出了一種改進的加權主成分分析法以解決質量工程中的多響應優化問題。在加權主成分分析法的基礎上，該方法將R2系數結合到主成分分析中，考慮了模型的預測能力，并可通過變換R2系數的標準化方式以強調或削弱預測能力對優化結果的影響，在多個響應模型的預測能力有顯著差異時該方法非常有意義。本文采用文獻中的實例進行數據分析，通過分析可以看出，本文提出的方法較加權主成分分析法具有一定優勢。

利用主成分分析法同時優化響應的均值和標準差，實現優化的穩健性是下一步研究的重點。

［1］Su C T，Tong L I.Multi-response robust design by principal component analysis［J］.Total Quality Management，1997，8(6):409-416.

［2］Antony J.Multi-response optimization in industrial experiments using Taguchi’s quality function and principal component analysis［J］.Quality and reliability engineering international，2000，16:3-8.

［3］鐘曉芳，韓之俊.利用主成分分析對多質量特性的優化設計［J］. 南京理工大學學報，2003，27(3):301-304.

［4］Liao H C.Multi-response optimization using weighted principal component［J］.The International Journal of Advanced Manufacturing Technology，2006，27:720-725.

［5］Gauri S K，Chakraborty S.Optimization of multiple responses for WEDM processes using weighted principal components［J］.The International Journal of Advanced Manufacturing Technology，2009，40:1102-1110.

［6］Shih J S，Tzen Y F，Yang J B.Principal component analysis for multiple quality characteristics optimization of metal inert gas welding aluminum foam plate［J］.Materials and Design，2011(32):1253-1261.

［7］Kim K J，Lin D K J.Simultaneous optimization of mechanical properties of steel by maximizing exponential desirability functions［J］.Applied Statistics，2000，49(3):311-325.

［8］Nair V N.Taguchi’s parameter design:a panel discussion［J］，Technometrics，1992，34:127-161.

［9］Richard A.Johnson，Dean W.Wichern著，陸璇，葉俊，譯.實用多元統計分析［M］.北京:清華大學出版社，2008.

Application of Improved Principal Component Analysis Method to the Multi-Response Optimization

ZHANG Ying-dong，HE Zhen
(College of Management and Economics，Tianjin University，Tianjin 300072，China)

An improved principal component analysis method，which takes into consideration the difference in the predictive ability among the responses is proposed.Principal component analysis method is a popular method for multi-response optimization.To consider the predictive ability，the proposed method applies R2coefficient which represents the degree of fit of the regression model to principal component analysis.Compared with the existing principal component analysis method，the proposed method can transform multi-response into single response，and consider the predictive ability.Case study shows that the results obtained through this method can reflect the impact of the predictive ability，the response with strong predictive ability is greatly improved.

quality engineering;multi-response optimization;principal component analysis;predictive ability

TH165;F406.3

A

1001-2265(2012)11-0097-04

2012-04-10

國家自然科學基金重點項目(70931004)

張迎冬(1986—)，男，河北張家口市人，天津大學管理與經濟學部碩士研究生，主要研究方向為質量工程、工業工程，(E-mail)pauldd@126.com。

(編輯 李秀敏)