基于滑移網格的臨近空間螺旋槳流場數值仿真

程鈺鋒，聶萬勝，胡永平

(1.裝備學院研究生院，北京懷柔 101416;2.裝備學院航天裝備系，北京懷柔 101416;3.河北滄州飛行訓練基地，河北滄州 061036)

0 引言

現今油價大幅上漲，節油成為飛行器設計中必須考慮的一個環節［1］。螺旋槳發動機因其在亞音速范圍內的節油優點引起了人們的普遍關注和高度重視，螺旋槳的研究工作也得到了進一步的發展。螺旋槳氣動性能的研究是螺旋槳動力系統研制工作的關鍵，國內外許多專家學者都采用計算流體力學(computational fluid dynamics，CFD)技術研究了螺旋槳的氣動性能，取得了很多有意義的成果。CFD是近三十年來迅速發展的技術，但它已經廣泛的滲入到社會和生活的各個方面，在研究流動現象、解決流體工程問題等方面發揮了重要作用，尤其在航空航天領域已成為不可或缺的核心技術之一［2］。

螺旋槳和旋翼流場的復雜性使得螺旋槳、旋翼CFD技術總體落后于固定翼CFD技術［3］。起初，人們采用小擾動勢方程法［4］研究螺旋槳的旋轉流場，但由于使用了小擾動的假設，只對于薄翼等擾動不太強的跨音速流動才能給出較好的結果。后來，有人采用全勢方程法［5-7］研究螺旋槳的旋轉流場，全勢方程求解的復雜程度介于歐拉方程和小擾動方程之間，在激度不太強的情況下，具有較好的模擬精度。為了更準確地模擬旋翼流場中出現的激波和旋渦流動，從20世紀80年代以來，許多研究以歐拉方程和N-S方程來求解旋翼流場［8］。我國的研究工作始于20世紀90年代。1993年，西北工業大學的楊國偉和何植岱［9］采用渦格升力面法，建立一種三維自由尾渦模型，構造一種松弛迭代法，計算得到了收縮尾渦。1996年，西北工業大學的王立群、喬志德等人［10-11］，采用網格中心有限體積法和五步Ruuge-Kutta(5，2)時間推進格式，通過求解三維歐拉方程，仿真得到了直升機旋翼懸停流場，在沒有任何尾跡模型的情況下，計算了兩旋翼在亞聲速和跨聲速時的壓力分布。1998年，上海交通大學的杜朝暉［12-13］為解決水平軸風力渦輪設計與性能預估方法存在失速延遲現象的問題，以旋轉葉輪三維邊界層方程為理論基礎，在分析了風力渦輪葉片表面產生失速延遲的機理后，建立了風力渦輪設計與評估方法的三維失速延遲修正模型，提高了水平軸風力渦輪的設計水平。20世紀初，國內關于螺旋槳氣動仿真的研究較少。2008年，中科院的聶營、王生等人［14-15］采用Gambit軟件對螺旋槳進行幾何建模，再用Fluent軟件基于滑移網格，仿真研究了臨近空間螺旋槳的氣動性能。2008年，西工大的許建華、宋文萍等人［16］采用雷諾平均N-S方程和嵌套網格技術對美國國家可再生能源實驗室的CER實驗型風力機葉片進行了仿真研究，湍流方程是B-L代數模型;計算中采用了有限體積空間離散法和改進型隱式LU-SGS時間推進格式，所用的嵌套網格技術有效的捕捉了螺旋槳的尾渦;在此基礎上，2009年［17］，他們采用在不同粗細網格上消除不同頻率誤差加速解的收斂的多重網格技術，仿真研究了螺旋槳側流粘性流場，其中多重網格采用非線性方程的全近似格式(FAS)。2010年，西工大的羅淞、楊永等人［18］采用多塊點對點網格生成技術，生成了螺旋槳的空間計算網格，分別研究了歐拉方程組和N-S方程組對不同進距比下螺旋槳運動過程的仿真結果，與實驗進行對比后得出歐拉方程比較適合于螺旋槳的工程設計。

臨近空間低速飛行器大多采用螺旋槳作為其動力裝置，螺旋槳氣動性能的優劣決定臨近空間低速飛行器的性能，因此，研究臨近空間環境下螺旋槳的氣動性能是十分迫切的工作，但臨近空間環境特殊，很難開展實驗研究［19］。基于此，本文采用滑移網格模型，考慮RNG k-ε湍流模型，通過求解三維非定常N-S方程，在驗證了數學模型可行性的基礎上，仿真研究了臨近空間螺旋槳非定常旋轉流場。仿真結果與文獻資料和理論分析一致，可以用于臨近空間螺旋槳的設計和研究。

1 數學模型

1.1 控制方程

對于N-S方程，連續方程、動力方程和能量方程的通用形式可以寫成如下形式。

其中:ρ是氣體密度，U是速度矢量，φ是通用變量，Γ是廣義擴散系數，S是廣義源項。對于連續方程、動力方程和能量方程，φ分別為1、ui和T;Γ分別為0、μ 和 k/cp;S分別為0、-?p/?xi和 ST。ui是速度分量，T是溫度，μ是粘性，k是流體的傳熱系數，cp是比熱容，ST是粘性耗散項，即流體的內熱源及由于粘性作用流體機械能轉換為熱能的部分。

理想氣體狀態方程為:

式中R是氣體常數。

1.2 湍流模型

RNG k-ε湍流模型是基于k-ε標準兩方程的湍流模型，采用一種叫做重正規化群的數學方法對N-S方程進行暫態推理得到的改進型k-ε兩方程湍流模型。它由V.Yakhot和S.A.Orszag于1986年提出并逐步完善的［20-21］，其基本思想是認為在流場中小渦是各項同性的，處于統計定常的和統計平衡的狀態。忽略浮力湍動能的RNG k-ε湍流模型的輸運方程如下:

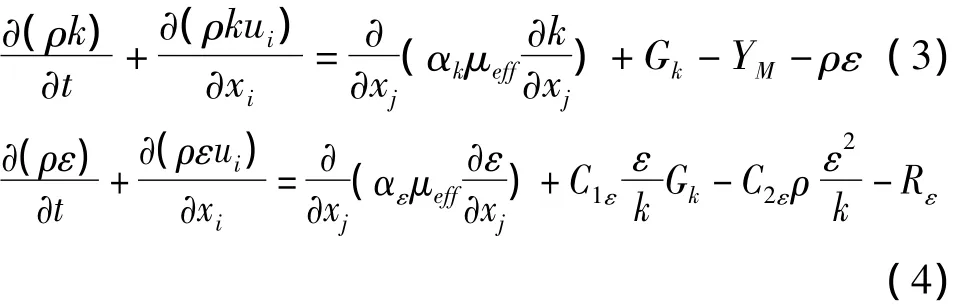
其中:k是湍流動能，ε是湍流耗散率;ui是速度分量，xi是坐標分量;αk=αε=1.393 分別是 Prandtl數對k和ε的反饋作用系數;ueff是有效粘性系數，Gk是由平均速度梯度引起的湍動能;YM是由于可壓縮湍流脈動膨脹對總的耗散率的影響;C1ε=1.42、C2ε=1.68是經驗常數;Rε是湍流模型中數的解析項。

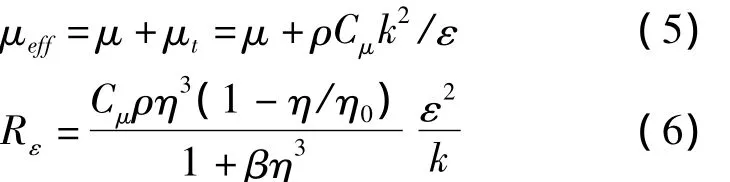
式中:Cμ=0.0845;η0=4.38;β =0.012;η =Sk/ε，S是漩渦大小。

由上可知，RNG k-ε湍流模型考慮了低雷諾數流動粘性，改進了標準k-ε模型的高雷諾數性質，并且提供了Prandtl數的解析公式，考慮了湍流漩渦，因此更加適合于雷諾數不是很高和帶有強漩渦運動狀態的數值仿真。

1.3 計算方法

采用耦合求解器，首先同時求解連續方程、動力方程和能量方程，然后求解湍流方程。耦合算法的流程比較簡單，如圖1所示。在耦合算法中使用隱式格式，即通過求解方程組的形式求解流場變量，它是使用塊 Gauss-Seidel法與 AMG法(Algebraic Multi-Grid，代數多重網格法)聯合完成的。

采用二階精度的有限體積AUSM(Advection Upstream Splitting Method)離散格式對粘性流體的控制方程和湍流方程進行空間離散。AUSM格式是20世紀90年代Liou和Stefen提出并完善的高分辨率迎風格式，融合了FVS穩定性好的優點和FDS高分辨率的優點，具有良好的數值穩定性和較高的間斷分辨率，其基本思想是認為對流波的傳播與聲波的傳播是物理上不同的過程，前者與特征速度u為線性關系，后者與特征速度u+a和u-a有非線性關系，將無粘通量分解為對流通量和壓力通量。詳見文獻［22］。

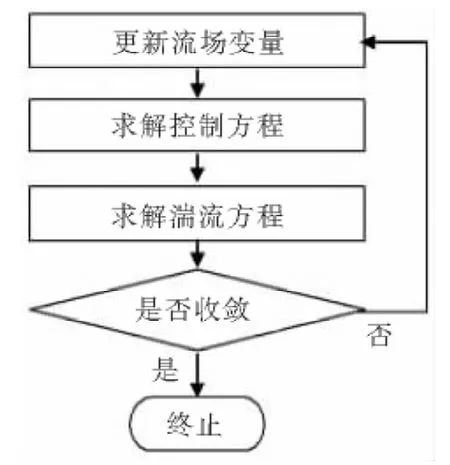
圖1 耦合算法流程圖

1.4 滑移網格模型

滑移網格是在動參考系模型和混合面法的基礎上發展起來的，常用于風車、轉子、螺旋槳等運動的仿真研究。在滑動網格模型計算中，流場中至少存在兩個網格區域，每一個區域都必須有一個網格界面與其他區域連接在一起。網格區域之間沿界面做相對運動。在選取網格界面時，必須保證界面兩側都是流體區域。

滑動網格模型允許相鄰網格間發生相對運動，而且網格界面上的節點無需對齊，即網格交界面是非正則的。在使用滑動網格模型時，計算網格界面上的通量需要考慮到相鄰網格間的相對運動，以及由運動形成的重疊區域的變化過程。

兩個網格界面相互重合部分形成的區域稱為內部區域，即兩側均為流體的區域，而不重合的部分則稱為“壁面”區域(如果流場是周期性流場，則不重合的部分則稱為周期區域)。在實際計算過程中，每迭代一次就需要重新確定一次網格界面的重疊區域，流場變量穿過界面的通量是用內部區域計算的，而不是用交界面上的網格計算。

下面，通過一個簡單的例子說明滑移網格是如何計算界面信息的。圖4是二維網格分界面示意圖，界面區域由面A-B、B-C、D-E和面E-F構成。交界區域可以分為a-d、d-b、b-e等。處于兩個區域重合部分的面為d-b、b-e和e-c，構成內部區域，其他的面(a-d、c-f)則為成對的壁面區域。如果要計算穿過區域IV的流量，用面d-b和面b-e代替面D-E，并分別計算從I和III流入IV的流量。

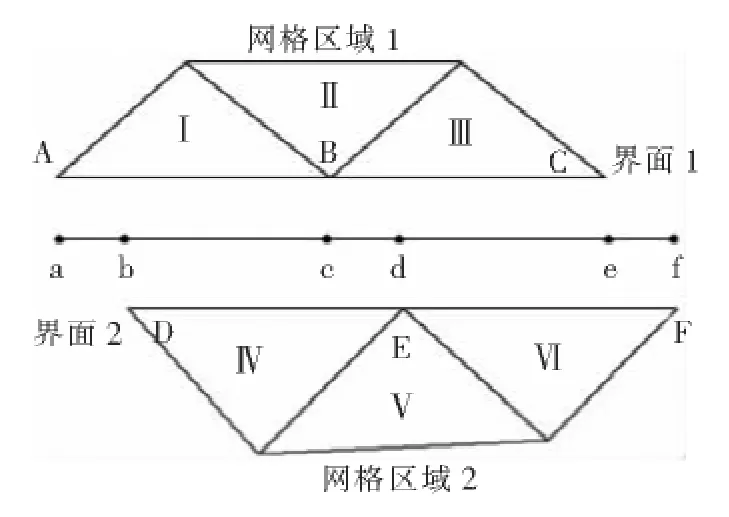
圖2 二維網格分界面示意圖

1.5 模型驗證

［15］，通過比較螺旋槳的靜拉力，驗證上述數學模型的可行性。螺旋槳的幾何建模及網格劃分在gambit環境下完成，直徑為28 in，螺距為10 in，具體尺寸詳見文獻［15］。

表1是文獻［15］的實驗和計算結果與本文計算結果的比較。由表1可見，文獻［15］的計算結果與實驗結果的最大誤差為20%，本文計算結果與實驗數據的最大誤差為15.8%，本文計算結果與實驗數據更為接近，說明本文所用計算模型是可行的。

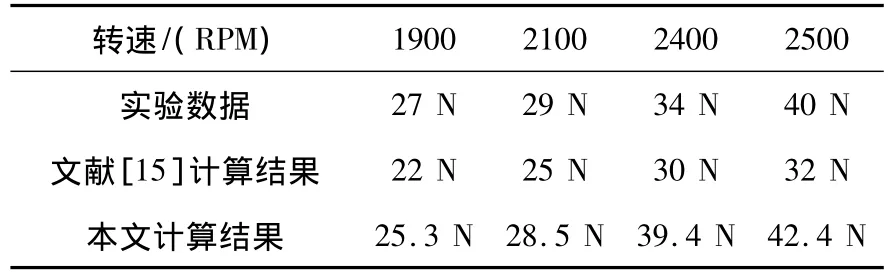
表1 靜拉力的比較

2 螺旋槳模型及網格

圖3是本文所研究的螺旋槳局部及其網格示意圖，螺旋槳葉素選擇Eppler 387翼型，不同槳徑處的葉素弦長和安裝角都相同且分別為0.05m和20°，螺旋槳直徑D為0.8 m，兩個槳葉之間的輪轂是長0.06 m、直徑0.03 m的圓柱體。計算區域是一個長10 D、直徑8D的圓柱體。速度入口距螺旋槳4D，給定氣流速度及總溫，壓力出口距螺旋槳6D，給定總溫和總壓;遠場距螺旋槳轉軸4D，給定氣流速度、總壓及總溫，如圖4所示。

由于滑移網格模型允許相鄰網格之間發生相對運動，而且網格界面上的點無需對齊，即網格是非正則的。利用這一特點，可以更好的分布網格的疏密度，既保證了計算流場所需要網格數又使網格總數減小，從而節約計算資源。對螺旋槳的仿真而言，螺旋槳近區域流場變化劇烈，所以應該加密網格，遠離螺旋槳的區域流場較為平緩，對網格數目要求不高，所以網格數目較少。

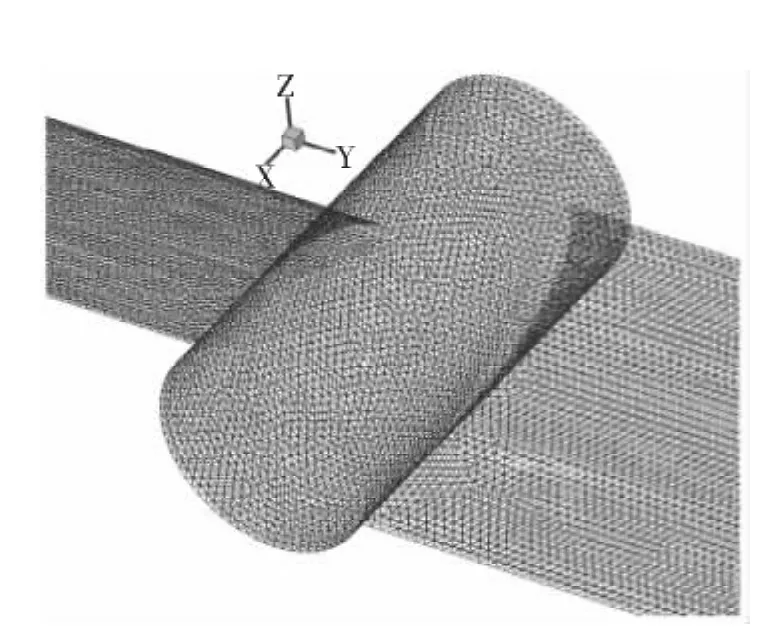
圖3 螺旋槳局部網格示意圖

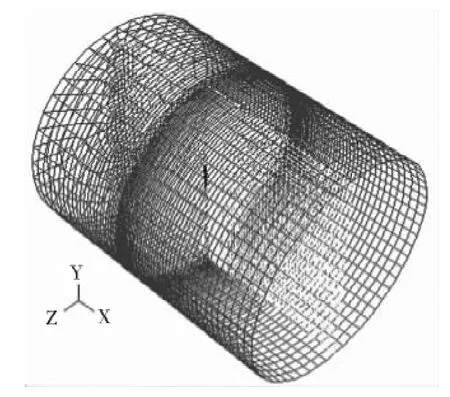
圖4 計算區域及網格示意圖

圖4是整個計算區域的網格示意圖。整個計算區域共分為3個小區域。旋轉區域是中間包圍螺旋槳的一個小區域，該區域網格為非結構網格，網格數約為60萬。旋轉區前后的兩個區域網格為結構網格，網格數約為12萬。

對螺旋槳的仿真而言，螺旋槳近區域流場變化劇烈，所以應該加密網格，遠離螺旋槳的區域流場較為平緩，對網格數目要求不高，所以網格數目較少。基于此，本文將計算區域分為氣流入口區域、旋轉區域和氣流出口區域3個小的計算區域。螺旋槳前后的氣流入口和出口區域采用TTM［23］方法生成結構網格，并在各自靠近螺旋槳的一端加密，網格總數約為12萬。旋轉區域采用TGrid網格劃分法生成非結構網格，螺旋槳表面網格節點之間距離為1 mm，網格總數約為60萬。

3 仿真結果及分析

本節在飛行高度為20 km，螺旋槳前進速度分別為5 m/s和20 m/s的條件下，對不同轉速下螺旋槳的運動過程進行仿真，分析螺旋槳拉力、效率隨轉速的變化規律及其原因，研究螺旋槳速度、渦流強度等參數在旋轉流場中的分布規律。

圖5是前進速度為5 m/s和20 m/s時，螺旋槳的拉力和效率隨其轉速的變化規律比較圖。其中螺旋槳的效率η=TV0/2pinsM，T是螺旋槳總拉力，M是總扭矩，ns是轉速，V0是螺旋槳的前進速度。由圖可見，當螺旋槳的前進速度不相同時，螺旋槳的氣動性能隨轉速變化而變化的規律相同，但總的氣動性能如拉力系數和效率還是有所差別，前進速度為20 m/s時拉力和效率比前進速度為5 m/s時稍大。由圖5(a)可見，在同一個前進速度條件下，螺旋槳拉力隨轉速的減小而減小;當轉速減小到一定的程度后，螺旋槳拉力變為負值，這是因為螺旋槳的工作狀態已經由前進狀態轉為制動狀態，此時螺旋槳不產生拉力，而產生與飛行方向相反的阻力。由圖5(b)可見，螺旋槳的氣動效率隨轉速的增大先增大后減小，與文獻［19］的分析結果一致。

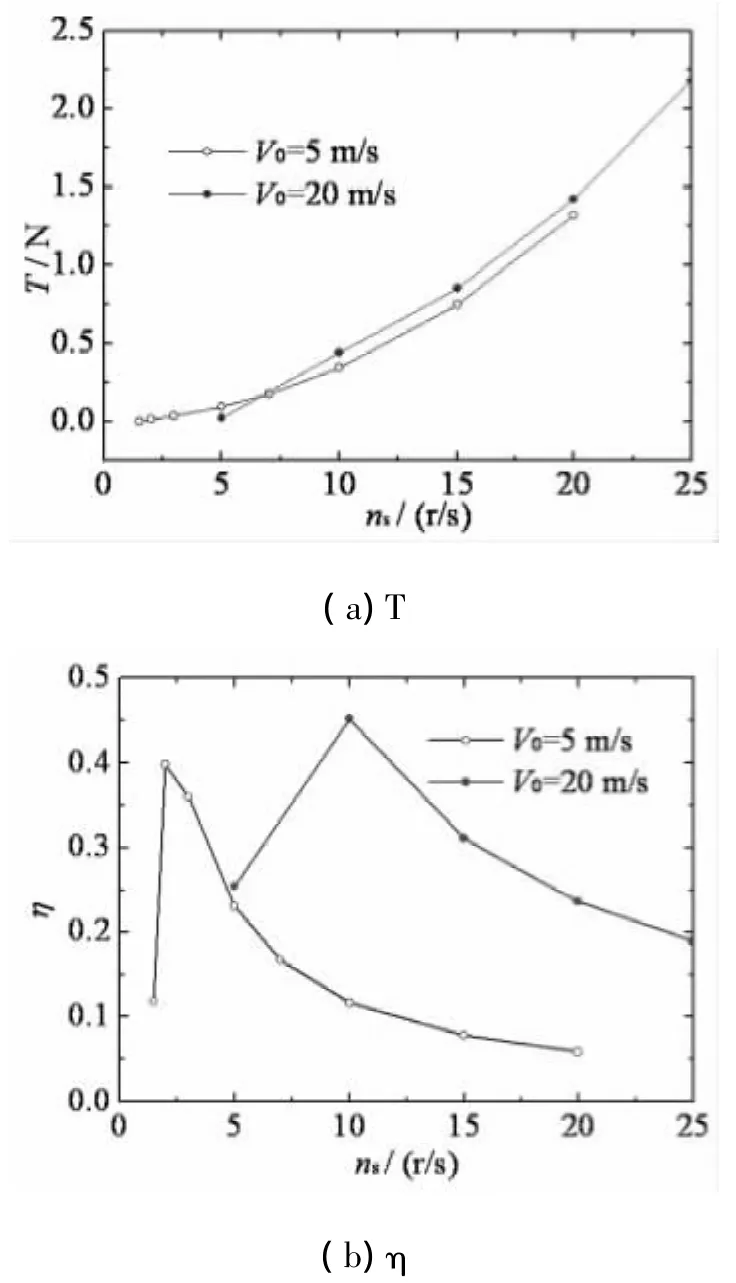
圖5 `拉力和效率隨進距比的變化

圖6是前進速度為5 m/s，轉速分別為60 rpm、180 rpm和1200 rpm時部分葉素周圍壓力系數分布比較圖，其中壓力系數Cp=2(p-p0)/ρV02，p 是流場壓力，p0是環境壓力。

圖6 前進速度為5 m/s時葉素拉力系數分布比較圖

由圖6(a)可見，當前進速度為5 m/s，轉速為60 rpm時，葉素吸力面壓力系數大于升力面壓力系數，即槳葉迎風面的壓力系數大于背風面壓力系數，說明該工況下槳葉產生與飛行方向相反的阻力，螺旋槳處于制動狀態。但壓力面和升力面的壓力系數差別不是很大，因此此時所產生的負拉力比較小，與圖5(a)所示一致。

由圖6(b)可見，當轉速增大到180 rpm時，螺旋槳的工作狀態已經由制動狀態轉向了前進狀態，葉素吸力面壓力系數小于升力面壓力系數，即槳葉背風面壓力系數大于迎風面壓力系數，螺旋槳產生與飛行方向一致的正拉力;在槳根部位葉素升力面和吸力面的壓力系數相差不大，隨著槳徑的延伸，在槳尖部位，葉素升力面壓力系數與吸力面壓力系數之間的差別越來越大，這是由于合成氣流的速度大小和攻角都隨著槳徑的延伸而逐漸增大的原因。

由圖6(c)可見，當轉速繼續增大到1200 rpm時，槳葉迎風面與背風面的壓力系數之差越來越大，但槳根部位葉素升力面和吸力面壓力之差依然很小;隨著槳徑的延伸，葉素升力面和吸力面壓力之差逐漸增大，當槳徑延伸到一定程度后，葉素升力面和吸力面壓力之差又逐漸變小，這可能是由于轉速增大，在槳尖部位存在誘導激波的原因。

比較圖6(a)、(b)、(c)可知，當前進速度不變，螺旋槳轉速增大時，葉素升力面和吸力面壓力之差越來越大，說明槳葉產生的拉力隨著轉速的增大逐漸增大。由葉素三角形理論［19］可知，當螺旋槳前進速度不變且轉速增大時，合成氣流相對于葉素的速度和攻角逐漸增大，因此槳葉產生的拉力逐漸增大，仿真結果與圖5(a)和理論分析一致。

圖7是螺旋槳前進速度為20 m/s，轉速分別為300 rpm、900 rpm和1500 rpm時，部分葉素周圍流線分布比較圖。由圖7(a)可見，當轉速為300 m/s時，從槳根到z=0.1 m處的槳徑區域，葉素處于負攻角狀態，說明有一部分葉素產生負拉力，這將減小螺旋槳的總拉力，從而降低螺旋槳氣動性能，導致氣動效率降低。由圖7(b)可見，當轉速增大為900 rpm時，螺旋槳槳根部位流動非常穩定，但從z=0.2 m處，槳葉表面開始出現流動分離現象，當槳徑繼續延伸時，分離現象逐漸加劇。流動分離的存在將會大大降低螺旋槳的氣動性能，尤其是降低螺旋槳的氣動效率。由圖7(c)可見，當螺旋槳轉速繼續增大到1500 rpm時，在z=0.1 m的槳徑部位，葉素周圍就開始出現了流動分離現象，而且分離渦隨著槳徑的延伸迅速增大，分離現象比轉速為900 rpm時嚴重很多，說明此時螺旋槳的氣動性能低于轉速為900 rpm時。因此，螺旋槳效率隨轉速先提高后降低的原因是:當轉速很小的時候，由于槳葉部分葉素處于負攻角狀態導致效率降低，當轉速很大時，由于槳葉部分葉素處于大迎角工作狀態，葉素表面流動分離嚴重，導致螺旋槳氣動效率降低。

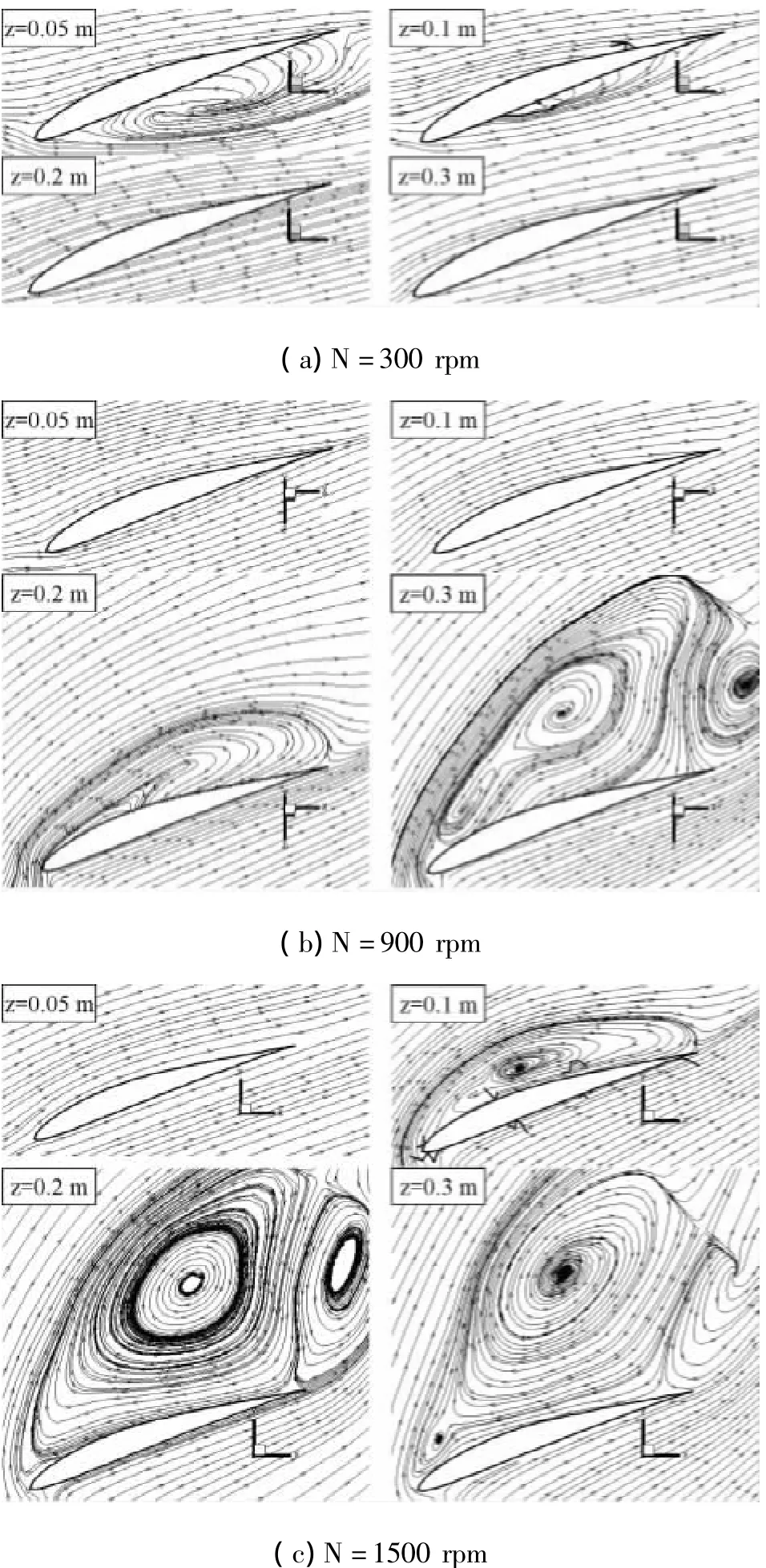
圖7 前進速度20 m/s時葉素周圍流線分布比較圖

圖8是前進速度為5 m/s，轉速分別為60 rpm、180 rpm和1200 rpm時，x=0的橫截面上，流場速度和渦流強度分布比較圖，其中速度單位為m/s，渦流強度的單位為1/s。由圖8(a)可見，當轉速為60 rpm時，流場的速度很小，槳尖部位的氣流速度甚至小于槳根部位的速度，且槳根部位速度場的分布范圍也大于槳尖部位;渦流強度與速度分布一樣，槳根部位的渦流強度大于槳尖部位。由圖8(b)可知，當轉速增大到180 rpm時，槳尖部位的速度大于槳根部位，槳尖部位速度場的分布范圍也大于槳根部位;渦流強度與速度分布一樣。由圖8(c)可見，當轉速繼續增大到1200 rpm時，槳尖部位的速度進一步增大，速度場的分布范圍也在增大，兩個槳葉速度場之間逐漸開始相互影響;渦流強度大小及分布與速度分布相同。比較圖8(a)、(b)、(c)可知，槳葉周圍速度及速度場的分布范圍，渦流強度及渦流強度分布范圍都隨轉速的增大而增大。

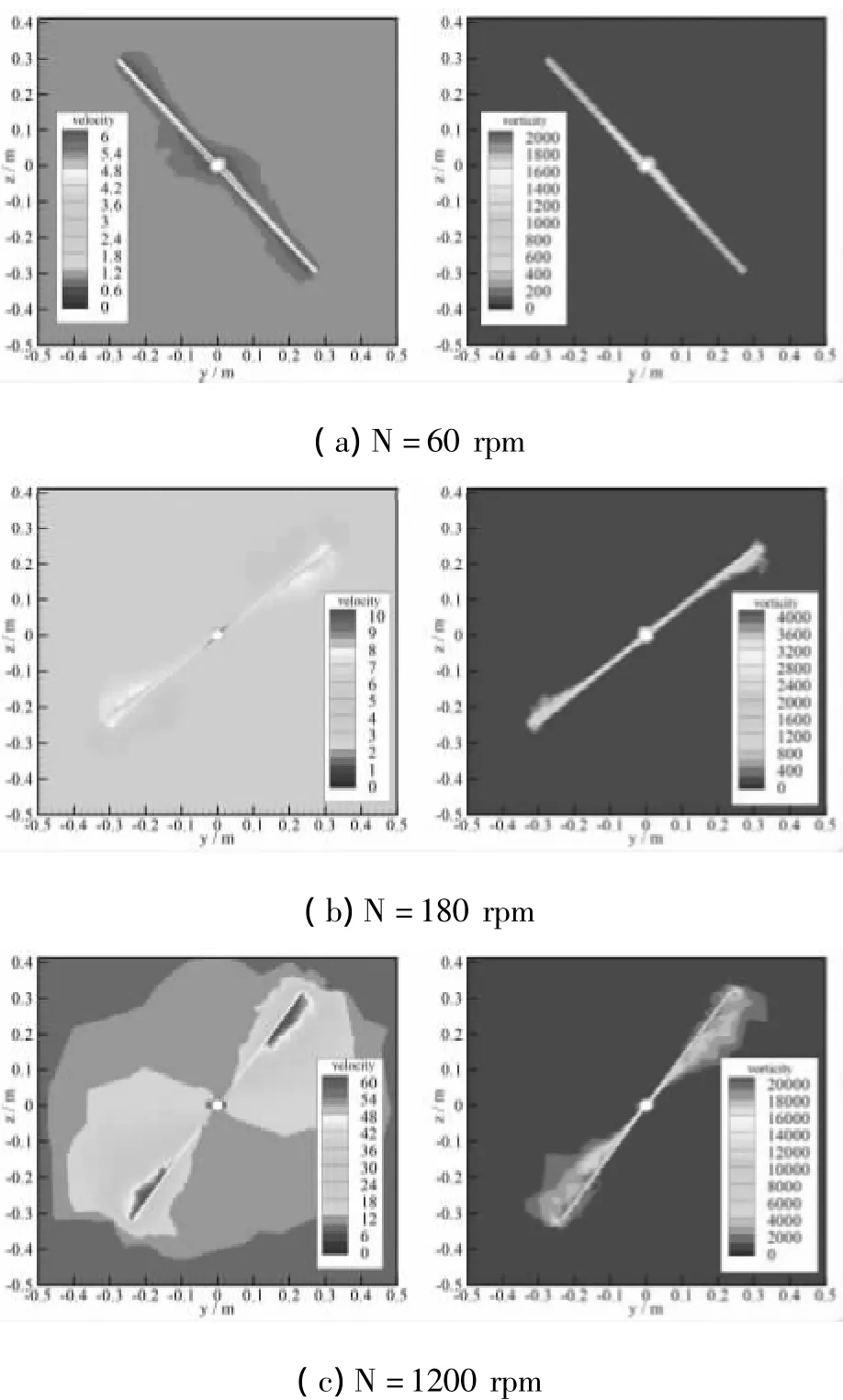
圖8 前進速度為5 m/s時x=0處速度和渦量分布比較圖

圖9是前進速度5 m/s、轉速1200 rpm時，流場速度分布沿氣流方向的演化圖，速度單位是m/s。螺旋槳中心位置在x=0的地方，因此x小于0的橫截面在螺旋槳前進方向，x大于0的橫截面在螺旋槳的后面。由圖可見，在螺旋槳的前面，由螺旋槳槳葉轉速運動產生旋轉誘導速度的影響范圍較小，在x=-0.2的地方速度場的分布范圍就已經比較均勻。當x逐漸增大至靠近螺旋槳，即靠近x=0的橫截面時，速度場的分布變得越來越不均勻，由槳葉旋轉運動產生的旋轉流場對氣流的影響越來越大，并且逐漸變成由旋轉誘導速度為主。在x=0的橫截面上誘導速度的影響范圍最大，最大誘導速度在螺旋槳槳尖部位。當x繼續增大時，旋轉誘導速度對氣流的影響又逐漸減小，至x=0.7 m處旋轉誘導速度的影響不明顯，可見在螺旋槳的后面，旋轉誘導速度的影響范圍遠大于前面的影響范圍。

4 結論

本文基于滑移網格模型，考慮RNG k-ε湍流模型，通過求解三維非定常N-S方程，在驗證了數學模型可行性的基礎上，仿真研究了螺旋槳非定常旋轉流場。所得流場清晰，速度、流線、渦流強度等流場參數分布正確，仿真結果與文獻資料和理論分析一致，可以用于臨近空間螺旋槳的設計和研究。主要結論有:

1)當螺旋槳前進速度不變，轉速增大時，合成氣流相對于葉素的速度大小和攻角逐漸增大，所以螺旋槳總拉力隨轉速的增大而增大。

2)當螺旋槳前進速度不變時，轉速很小則有一部分槳葉葉素處于負迎角狀態，導致效率降低;轉速很大則有一部分槳葉葉素處于大迎角狀態，葉素表面流動分離嚴重，導致效率降低;所以螺旋槳的效率隨轉速的增大先提高后降低。

3)槳葉周圍速度大小及速度場的分布范圍、渦流強度大小及渦流強度分布范圍都隨轉速的增大而增大。

4)槳葉旋轉運動產生的誘導速度對螺旋槳前面流場的影響范圍較小，對螺旋槳后面流場的影響范圍較大。

參考文獻:

［1］Arne S.Unsteady CFD Simulations of Contra-Rotating Propeller Propulsion Systems［C］//Hartford，44th AIAA/ASME/SAE/ASEE Joint Propulsion Conference＆Exhibit.2008，AIAA 2008-5218.

［2］閻超，于劍，許晶磊，等.CFD模擬方法的發展成就與展望［J］.力學進展，2011，41(5):562-589.

［3］徐國華，招啟軍.直升機旋翼計算流體力學的研究進展［J］.南京航空航天大學學報，2003，35(3):338-344.

［4］Caradonna F X，Dessopper A，Tung C.Finite difference modeling of rotor flow including wake effects［J］.Journal of the American Helicopter Society，1984，29(2):86-33.

［5］Chang I C.Transonic flow analysis for rotors，Part 1:Three-dimensional quasi-steady full-potential calcula-tion［R］.NASA TP-2375，1984.

［6］Egolf T A，Sparks S P.A full potential rotor analysis with wake influence using all inner-outer domain techmque［C］.//In the 42th AHS Annual Forum，1986.

［7］Steinhoff J，Ramachandran K.Free wake analysis of compressible rotor ftows［J］.AIAA Journal，1990，88(3):426-431.

［8］王適存，徐國華.直升機旋翼空氣動力學的發展［J］.南京航空航天大學學報，2001，33(3):203-211.

［9］楊國偉，何植岱.計及尾渦收縮的螺旋槳滑流計算［J］.空氣動力學學報，1995，13(1):83-86.

［10］王立群，喬志德，鐘伯文.直升機旋翼懸停流場的歐拉方程計算［J］.空氣動力學報，1998年，16(3):282-287.

［11］王立群，喬志德，張茹.直升機旋翼懸停流場的歐拉方程計算［J］.西北工業大學學報，1998年，16(4):594-598.

［12］杜朝暉.水平軸風力渦輪設計與性能預估方法的三維失速延遲模型 -Ⅰ理論基礎［J］.太陽能學報，1999，20(4):392-397.

［13］杜朝暉.水平軸風力渦輪設計與性能預估方法的三維失速延遲模型-Ⅱ模型建立及應用［J］.太陽能學報，2000，21(1):1-5.

［14］聶營，王生，楊燕初.螺旋槳靜推力數值模擬與實驗對比分析［J］.計算機仿真，2009，26(3):103-107.

［15］聶營.平流層飛艇高效螺旋槳設計與試驗研究［D］.中國科學院光電研究所碩士學位論文，2008.

［16］許建華，宋文萍，韓忠華.基于嵌套網格技術的風力機葉片繞流數值模擬［J］.太陽能學報，2010年，31(1):91-94.

［17］許建華，宋文萍，韓忠華，楊旭東，基于CFD技術的螺旋槳氣動特性研究［J］.航空動力學報，2010年，第25卷第5期，1103-1109.

［18］羅淞，楊永，左歲寒.螺旋槳流場Euler/NS數值解對比分析［J］.航空計算技術，2011，41(1):74-77.

［19］程鈺鋒，聶萬勝.臨近空間螺旋槳氣動性能分析［J］.直升機技術，2011，168:8-13.

［20］Yakhot V，Thangam S，Gatski T B，Orszag S A，Speziale C G.Development of Turbulence Models for Shear Flows by a Double Expansion Technique［R］.NASA Contractor Report 187611，ICASE Report No.91-65.

［21］Rubinstein R. Renormallzation Group Theoryof Bolgiano Scaling in Boussinesq Turbulence［R］.NASA Technical Memorandum 106602，ICOMP-94-8;CMOTT-94-2.

［22］Scandaliato A L.AUSM-based high-order solution for euler equations［C］//48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition 4-7 January 2010，Orlando，Florida，AIAA 2010-719.

［23］Thompson.J.F.，Thames.F.C.，Martin.C.W.Automatic Numerical Generation of Body-Fitted Curvilinear Coordinate System for Field Containing Any Number of Arbitrary Two-Dimensional Bodies［J］.J.Comput.Phys.1974(15):299-399.