滾動汽車輪胎自激振動仿真及其影響因素分析

左曙光，蘇 虎，王紀瑞

(同濟大學 汽車學院，上海 201804)

自激振動是指振動系統通過本身的運動，不斷地向振動系統內饋送能量，完全依靠本身的運動來激勵的一種運動形式，與外界激勵無關。

國內在自激振動方面的研究主要體現在分析分段光滑非線性自激振動方面，包括重型機床的“爬行”、機床切削的顫振、火車的“蛇行”運動、流固禍聯系統的自激振動、飛機的顫振以及具有間隙的系統的自激振動等。龔慶壽［1］指出機床以及液壓系統的“爬行”是由摩擦引起的自激振動現象，并對自激振動產生爬行的機理進行了分析，通過建立進給系統運動模型，對爬行現象進行了理論分析，進而得出了摩擦力的變化是產生爬行的原因，并給出了抑制和消除機械系統爬行的解決辦法。

國外專家學者對于自激振動的研究主要包括由風所引起的橋的自激振動、干摩擦引起的自激振動、氣流壓力引起的桅桿的自激振動、石油開采鉆井設備的分段非連續自激振動、峰鳴現象等等。其中Keele大學力學系的Mcmilla［2］針對峰鳴現象對干摩擦引起的自激振動進行了分析，指出峰鳴現象是一種自激振動，這種振動是在像車輪、琴弦類的物體當中由于干摩擦驅動力而引起的，其振動機理是很難定義的，并且通過將靜摩擦和動摩擦結合在一起的方式提出了一種振動模型，結果表明該模型能較好地解釋蜂鳴現象。

在輪胎自激振動方面，日本Sueoka［3］研究小組，將兩個相接觸的旋轉滾輪之間產生自激振動的原理用于研究汽車輪胎周向多邊形磨損現象，解釋了可能產生周向規則多邊形磨損的原因，然而文中卻沒有考慮懸架形式、車輪側偏角與外傾角、輪胎與路面相互作用等因素的影響。同濟大學汽車學院在此基礎［3］上進一步開展研究，通過對自激振動模型的穩定性進行研究，找出了產生規則輪胎多邊形磨損的行駛車速范圍［4－5］。然而以上研究都忽視了胎面與路面之間動摩擦系數與靜摩擦系數相互轉化時對自激振動以及多邊形磨損的影響，也沒有對各參數進行靈敏度分析。因此，本文先對自激振動機理進行闡述，然后結合輪胎三維有限元模型，采用能綜合體現動、靜態摩擦特性的LuGre摩擦模型，基于大型有限元分析軟件MSC.Marc，對輪胎多邊形磨損中自激振動的規律以及影響因素進行研究，為有效降低因多邊形磨損引起的輪胎報廢數量，合理設計和匹配車輛參數提供依據。

1 輪胎自激振動有限元模型

1.1 胎面自激振動機理分析

為分析胎面在側向上的自激振動，以單自由度振動模型為例，將胎面離散化為若干集中質量塊，限制各質量塊僅有沿輪胎寬度方向上的線自由度，并且在相鄰質量塊間存在著彈簧和阻尼的作用。取任一接地質量塊作為研究對象，建立胎面－路面單自由度理論模型，如圖1所示。

為考慮接地胎面側向的自激振動現象，將模型中的輪胎假設為靜止物體，而將此模型中的路面設為運動的，即在沿著輪胎的寬度方向上路面與輪胎之間存在一定的相對速度。胎面僅有一個側向平動自由度，與輪胎之間可看作是帶阻尼的彈簧連接，彈簧剛度Ks即為輪胎的側向剛度，阻尼器阻尼Cs即為輪胎的側向阻尼，接地胎面的質量m由接地印跡面積與胎面的厚度確定。

在汽車前進過程中，由于前束角的存在，輪胎在側向方向上會獲得一定的速度輸入。設前束角為θ，將汽車前進速度V分解到側向上，得到輪胎在側向上相對于地面的線速度Vb:

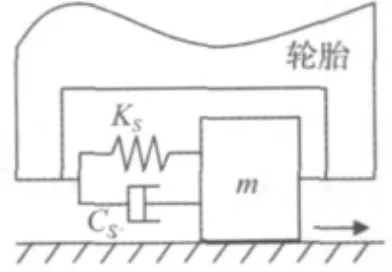
圖1 輪胎－路面單自由度模型Fig.1 Model of vibration of single degree of freedom between road surface and tire tread

在模型中，胎面振動能量的輸入來源于胎面與地面之間持續不斷的摩擦力作用，即兩者之間的相對速度變化是激勵源。為了便于分析，將輪胎與地面間的平動Vb簡化為皮帶輪的轉動。簡化后的模型如圖2所示。

設胎面質量塊m在皮帶上相對于初始位置(即彈簧及阻尼器不受力時的位置)的位移為 s，質量塊 m與皮帶間的相對速度Vr為:

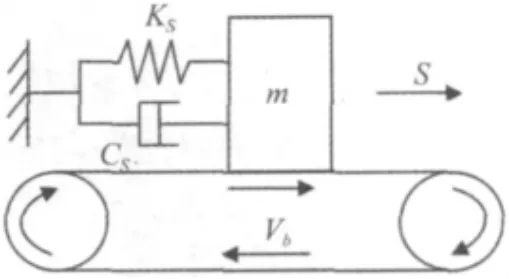
圖2 胎面質量塊鏈接簡化模型Fig.2 Simplified interlinking model of tire tread mass element with road surface

根據牛頓－歐拉運動學方程，可以列出胎面質量塊m側向振動的動力學方程如下:

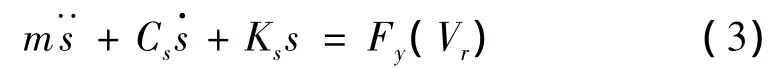
式中Fy(Vr)為胎面所受的側向力，是由輪胎接地處摩擦力引起的，是物體與皮帶輪間相對速度Vr的函數:

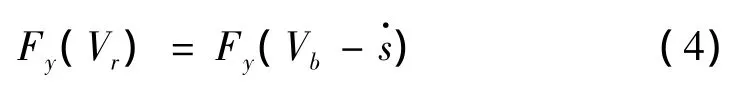
將Fy(Vr)在任意速度Vr處進行一階泰勒展開，得:

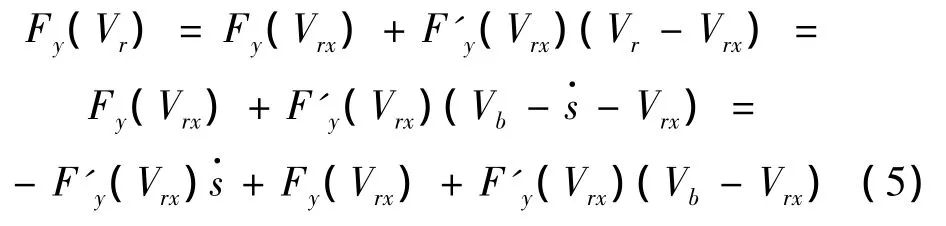
將式(5)代入式(3)，略去與振動無關的常數項并整理，得到在物體與皮帶輪之間的相對速度Vr=Vrx時的瞬時振動微分方程:

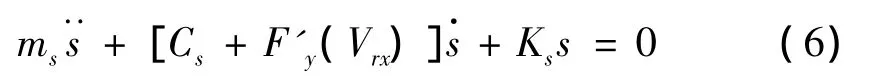
此時，該振動系統的當量阻尼為:

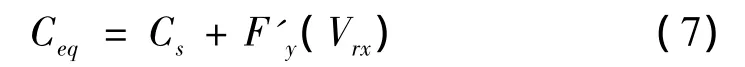
根據Ceq值的不同，對于該系統有如下討論:

① 正阻尼狀態:當Ceq＞0時，F'y(Vrx)＞－Cs，該振動系統處于正阻尼狀態，系統的能量被損耗，振動有衰減趨勢;

② 無阻尼狀態:當Ceq=0時，F'y(Vrx)=－Cs，該振動系統處于無阻尼狀態，系統的總能量不變，維持等幅振動;

③ 當 Ceq＜0時，F'y(Vrx)＜－Cs，該振動系統處于負阻尼狀態，系統從外界吸收能量，振動有增強的趨勢。

對于不同的摩擦模型，摩擦力曲線在Vr=Vrx處的斜率F'y(Vrx)并不相同，尤其在摩擦模型曲線的“負斜率”特性階段，此時F'y(Vrx)為負值。因此，若阻尼器的阻尼Cs很小，輪胎－路面干摩擦振動系統的當量阻尼Ceq會隨著相對滑動速度Vr的變化而在正值和負值之間不斷變換，使得該振動系統時而吸收能量時而消耗能量，呈現動態平衡，維持穩定的等幅振動，即形成自激振動。

對于干摩擦振動系統來說，摩擦特征曲線中的負斜率部分是形成自激振動的根本原因。若此負斜率部分足以抵消振動系統自身的正阻尼，則該振動系統便會表現出整體負阻尼狀態，進而產生自激振動;而若摩擦特征曲線的負斜率特征不明顯，或者振動系統自身的正阻尼比較大，則該振動系統無法出現整體負阻尼狀態，振動將被衰減，因此無法形成自激振動。為此本文將根據理論分析模型，考慮輪胎三維特性，結合LuGre摩擦模型，利用有限元方法對輪胎胎面自激振動現象進行研究。

1.2 輪胎三維有限元模型

正確建立輪胎的三維模型是進行高速滾動輪胎自激振動仿真的關鍵，考慮橡膠的非線性、簾線與橡膠復合材料的各向異性、輪胎大變形導致的非線性邊界條件以及滾動慣性對輪胎滾動特性的影響，建立了三維子午線輪胎非線性有限元模型。如圖3所示，子午線輪胎由胎面、胎側、胎肩、簾布層、帶束層和胎緣組成。本文的建模思路是先生成輪胎截面的二維結構，再應用MSC.Marc提供的3D軸對稱擴展作業功能實現二維單元的軸對稱三維擴展，最終生成如圖4所示的三維輪胎實體模型［6］。

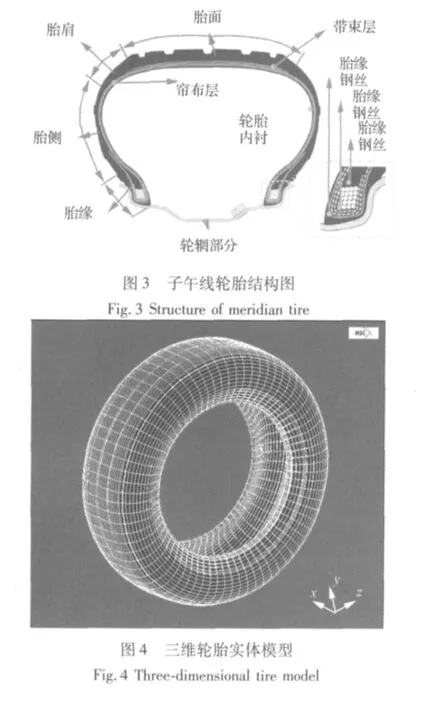
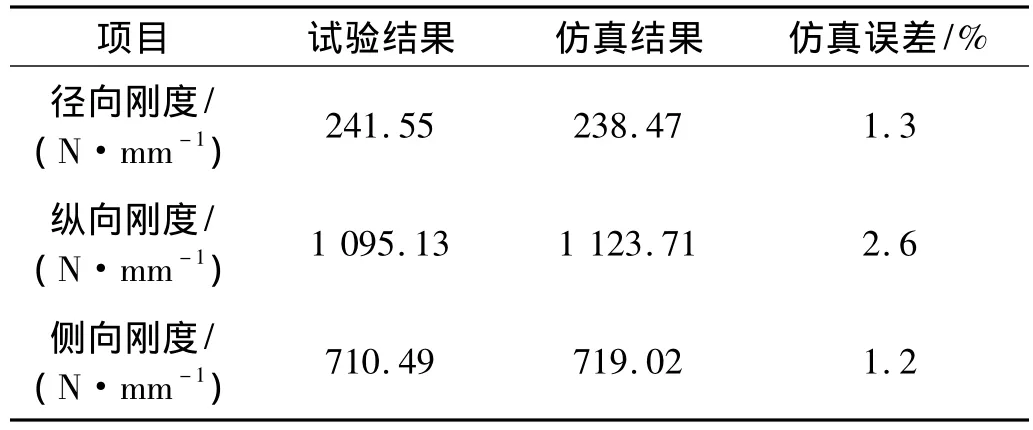
表1 輪胎三向剛度仿真與試驗結果比較表Tab.1 Comparison between experimental results and simulation data on tire stiffness in three directions

在對輪胎的不同結構部分進行材料和單元類型的定義之后，為了驗證模型的正確性，將模型各方向的仿真剛度值(徑向、縱向和側向)與實驗值進行對比，對比結果如表1所示［7］。可見仿真誤差都小于5%，在工程允許范圍內，滿足后續仿真要求。

1.3 LuGre摩擦模型及其二次開發

準確地再現輪胎與路面之間力的傳遞情況，對研究輪胎自激振動現象至關重要。經過對比不同摩擦模型［8］的特性后發現，Canudas等［9］提出的 LuGre 摩擦模型能很好地反映摩擦過程中的“負斜率”區間以及實際摩擦接觸過程中摩擦特性的動態變化現象。如圖 5所示，LuGre摩擦模型假設組成干摩擦副的兩物體間有無數的刷毛，并將這些刷毛看作是彈簧，摩擦力則產生于這些彈簧的彈性變形。當兩物體間有相對速度時，這些刷毛最初會表現出彈簧的性質，出現彈性變形而產生靜摩擦力，而后隨著彈性變形的不斷增大，在某一瞬間刷毛將會相對接觸面產生滑移，即產生動摩擦力。

本文應用MSC.Marc提供的UFRIC用戶子程序接口，用Fortran語言對LuGre摩擦模型進行了二次開發，并實現了與MSC.Marc的鏈接，為后面定義輪胎與路面之間的摩擦接觸奠定了基礎。

1.4 滾動輪胎自激振動仿真模型

在輪胎3D模型和LuGre摩擦模型建立完成后，為了更好地反映輪胎與路面的實際接觸狀態，針對本次仿真使用的子午線輪胎(型號為195/65R14)，本文將剛性路面用半徑為3.17 m(約為輪胎半徑的10倍)的圓環帶表示，因為實際路面也不能保證完全平整，本文所取的半徑值已經遠超過國標GB/T 18276－2000對滾筒半徑的要求，故仿真結果能反映實際路面和胎面的接觸情形。最后將輪胎模型－路面模型－摩擦模型整合成滾動輪胎仿真模型，如圖6所示。

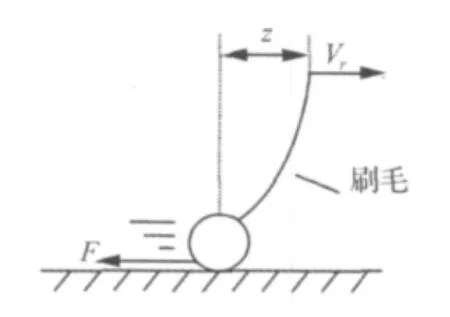
圖5 LuGre摩擦模型的物理模型Fig.5 LuGre friction model

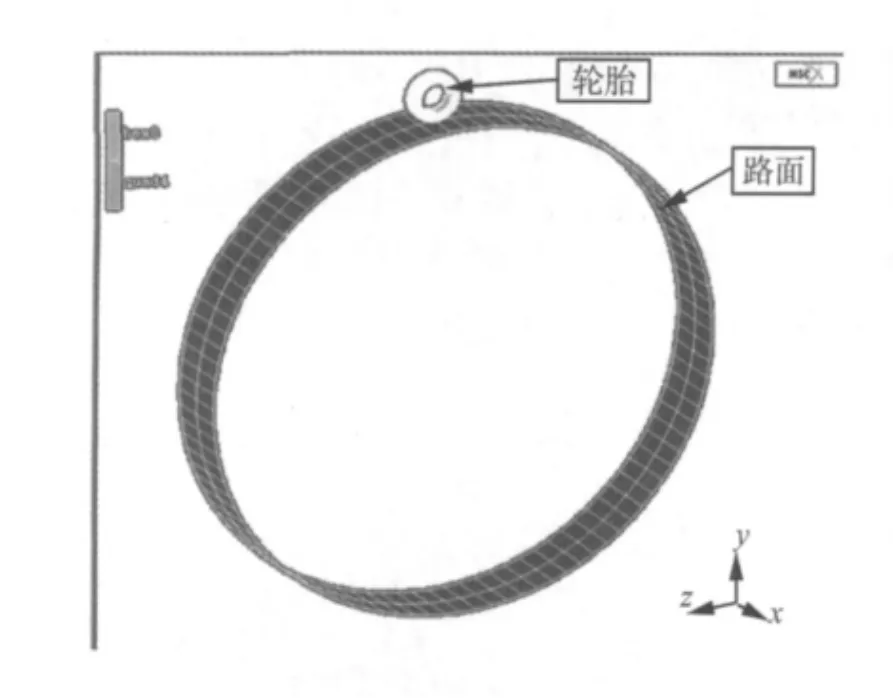
圖6 MSC.Marc中輪胎－路面整合模型Fig.6 Interlinking model of tire tread and road surface in MSC.Marc

2 輪胎的工作條件對自激振動特性影響仿真分析［10－12］

在正式仿真前，要定義邊界條件和載荷工況，這里將輪胎定義為可變形體，將路面和輪輞定義為剛性不可變形體。輪胎和輪輞之間定義為粘結接觸(GLUE)，輪胎和路面之間定義為摩擦接觸，摩擦模型選用上文通過Fortran語言二次開發建立的LuGre摩擦模型。

輪胎充氣狀態采用在輪胎的內壁上施加均勻分布的面載荷進行模擬;垂向接觸力采用限制輪胎輪輞的垂向位移，并在路面中心施加一個指向輪胎輪輞中心的垂向作用力進行模擬。

本次仿真，模擬實際試驗中的底盤測功機情形，即動力由路面輸入，使路面以一定的角速度轉動，通過路面與輪胎之間的摩擦接觸模型產生摩擦力，帶動輪胎轉動，實現輪胎的滾動。如圖7所示，對于輪胎，我們約束住了輪輞的三向平動自由度;對于剛性路面，約束了x和z兩向平動自由度，釋放y向平動自由度用于施加路面與輪胎的接觸擠壓。

同時，在路面轉動控制中心點的上方取一點，并把該點作為路面剛體運動控制的輔助控制節點。路面的中心控制節點用來施加路面剛體的平動邊界條件及平動載荷，輔助控制節點與中心控制節點聯合起來作用，以精確實現路面的轉動運動控制。

定義完邊界條件和載荷工況后，就要進行實際的輪胎滾動仿真分析，仿真所用參數如表2所示。

2.1 某一固定參數下輪胎胎面自激振動仿真分析

在表2參數下，輪胎滾動過程中某一工作步時的變形模型如圖8所示。為研究胎面的自激振動現象，選取胎面上一點，提取出其在輪胎胎面x方向(側向)上的側向振動位移時域信號，見圖9，同時提取輪胎胎面x方向(側向)上的側向振動速度時域信號，見圖10，以及胎面與路面之間的側向力時域變化曲線，見圖11。

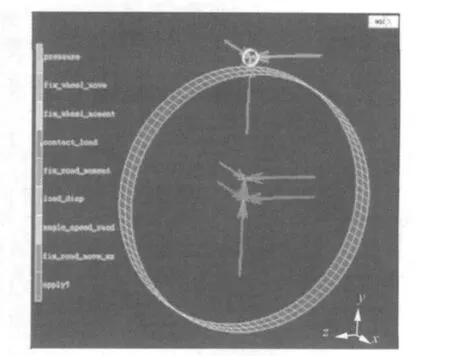
圖7 輪胎和路面約束條件Fig.7 Constrains in tire-road model

表2 仿真所用參數表Tab.2 Simulation parameters

圖8 輪胎滾動過程中模型圖Fig.8 Rolling tire model

從圖中可以看出:

(1)胎面的側向位移信號、側向速度信號以及路面的側向力信號都呈現周期性，這是由輪胎滾動的周期性所致，并且三者最終都趨于穩定;

(2)輪胎的側向力幅值大小大致為100～200 N，這與課題組前期的研究成果相一致［9］;

(3)胎面的側向位移信號、側向速度信號以及路面的側向力信號在路面接觸點處都有比較大的振動現象。

由于輪胎胎面的側向位移信號、側向速度信號以及路面與胎面之間的側向力信號的頻率成分都比較復雜，為了分析清楚其信號成分，有必要進行相應的頻域分析，觀察其頻域特征。圖12～圖14所示分別為胎面的側向位移、側向速度以及路面與胎面之間的側向力信號的頻域特性曲線及局部放大圖。

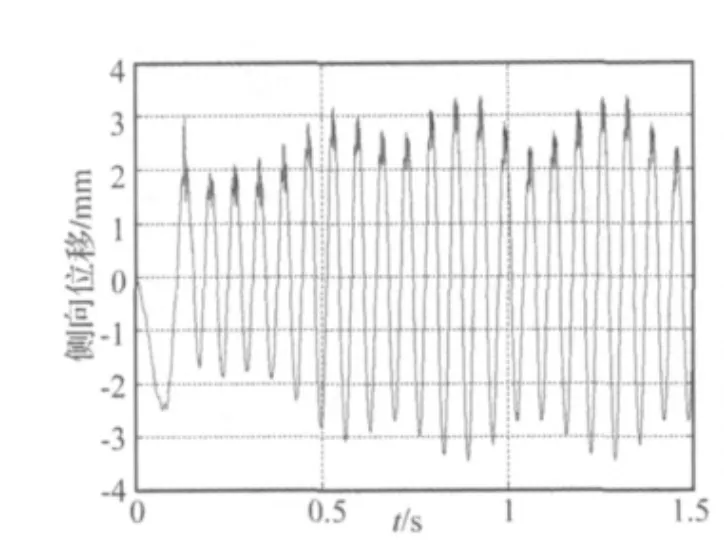
圖9 胎面側向振動位移Fig.9 Lateral tire tread vibration displacement

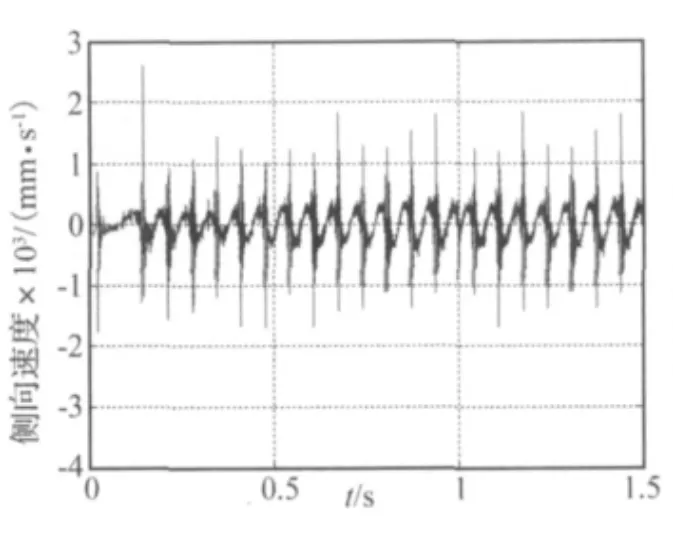
圖10 胎面側向振動速度Fig.10 Lateral tire tread vibration velocity

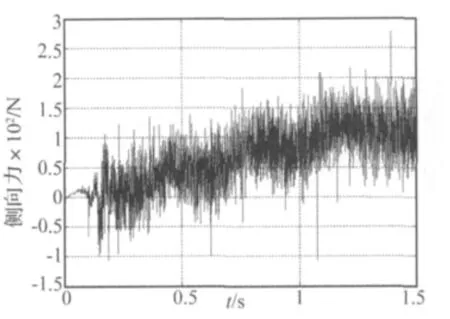
圖11 路面與胎面之間的側向力Fig.11 Lateral force between road surface and tire tread

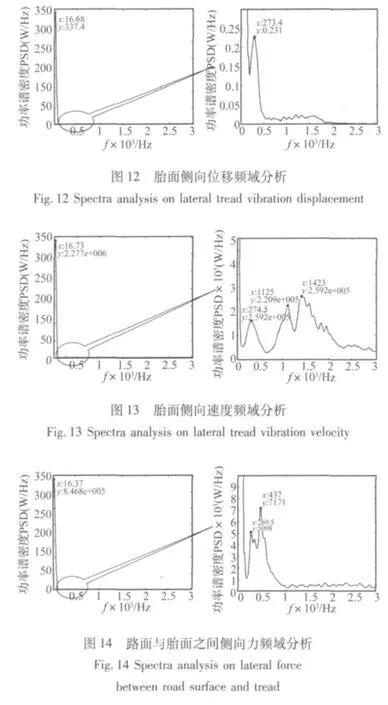
由頻域分析圖可以看出，在胎面的側向位移、側向速度和路面的側向力信號均包含頻率約為275 Hz的振動。另外，信號中有一能量比較高的低頻振動成分，頻率約為16～17 Hz，經計算該頻率為此車速下的輪胎滾動頻率。

表3～表6為在其他參數保持不變情況下，單獨改變車速、載荷、前束角和外傾角時自激振動頻率的變化情況。考慮到有限元仿真的數值誤差，可知該頻率與外界條件無關，僅由系統自身條件決定，類似于物體的固有頻率。

2.2 輪胎胎面自激振動影響因素分析

輪胎多邊形磨損和輪胎的自激振動是一個復雜的過程。為探討汽車行駛工況參數(車速和載荷)和車輪定位參數(前束角、外傾角)對輪胎側向自激振動的影響規律，本文將應用上文中的滾動輪胎仿真模型分別對其進行分析，找出各因素的影響規律，從而為控制輪胎的多邊形磨損提供依據和指導［11－12］。

表3 車速變化而其他參數不變時的自激振動頻率(“－”表示沒出現自激振動)Tab.3 Values of the tire self-vibration frequencies with the change of speed while other parameters keep constant(“－”denotes that there is no self-vibration)

表4 載荷變化而其他參數不變時的自激振動頻率(“－”表示沒出現自激振動)Tab.4 Values of the tire self－vibration frequencies with the change of load while other parameters keep constant(“－”denotes that there is no self-vibration)

表5 前束角變化而其他參數不變時的自激振動頻率(“－”表示沒出現自激振動)Tab.5 Values of the tire self-vibration frequencies with the change of car toe-in angle while other parameters keep constant(“－”denotes that there is no self-vibration)

表6 外傾角變化而其他參數不變時的自激振動頻率Tab.6 Values of the tire self-vibration frequencies with the change of camber while other parameters keep constant

2.2.1 自激振動強弱指標K

為了易于研究輪胎自激振動隨車速的變化趨勢，這里定義一個能反映自激振動強弱的系數K，即:

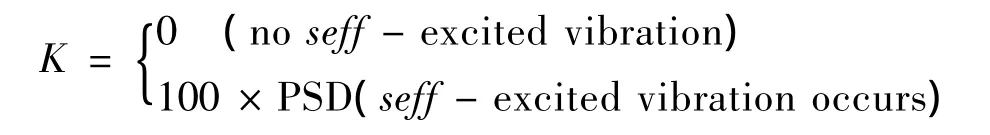
式中PSD為輪胎在自激振動頻率(或共振頻率)處的功率譜密度，當輪胎不產生自激振動時，定義K=0;當輪胎產生自激振動時，K值越大則表示自激振動越劇烈。

2.2.2 汽車行駛車速對輪胎自激振動的影響

考慮到輪胎的多邊形磨損主要出現在高速公路上，所以在仿真過程中，車速值不小于30 km/h;同時考慮到實際中汽車的行駛速度范圍，車速值也沒有必要取得過大，這里選取的車速值不大于250 km/h，仿真車速見表7。

表7 仿真用車速Tab.7 Simulation velocity used

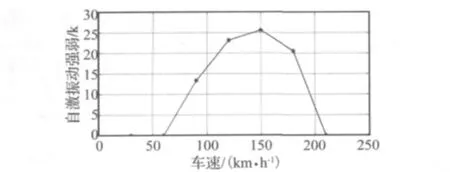
圖15 車速對輪胎自激振動的影響Fig.15 Impact of speed on tire self-excited vibration

圖15為不同車速下的K值，由圖可知，汽車的行駛速度對于輪胎胎面的自激振動有著重要影響，車速不同，自激振動產生與否以及自激振動的強弱程度均有所不同。在表2參數下，只有當車速在60～210 km/h范圍內時，輪胎胎面才能產生自激振動，車速過低或者過高時均不能產生。同時，在自激振動的車速范圍內，隨著車速的增加，自激振動先越來越劇烈，在達到一定車速時(本仿真條件下，車速大約在150 km/h)，再隨著車速的增大，自激振動劇烈程度越來越低，直到輪胎胎面自激振動消失，這與實際情況基本一致。

2.2.3 汽車載荷對輪胎自激振動的影響

為了研究汽車實際運行中的載荷大小對于輪胎的自激振動有著怎樣的影響，下面將選取汽車常用的載荷工況進行對比仿真分析。仿真中的載荷變化情況見表8。

圖16為不同載荷下的K值，由圖可知，汽車的載荷條件對輪胎胎面的自激振動有著重要影響，在一定工況和參數條件下，隨著載荷的增加，輪胎胎面的自激振動劇烈程度有增大趨勢。所以車輛在實際行駛中，以滿載或超載工況行駛的時間和路程越長，輪胎的多邊形磨損越嚴重，已經產生多邊形磨損的輪胎的報廢速度也越快。

表8 仿真用載荷Tab.8 Simulation load used

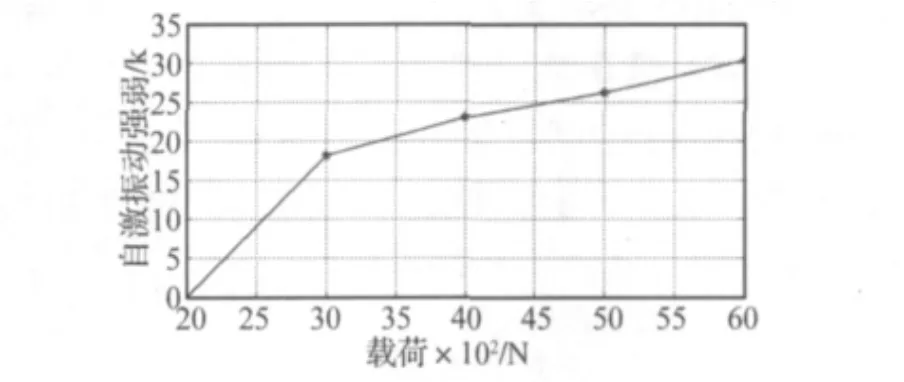
圖16 載荷對輪胎自激振動的影響Fig.16 Impact of load on tire self-excited vibration

2.2.4 汽車前束角對輪胎自激振動的影響

為了保證汽車具有良好的轉向特性和行駛特性，汽車轉向輪設置有車輪外傾角、車輪前束角、主銷內傾角和主銷后傾角等四個定位參數。由于定位參數特別是車輪外傾角和前束角的存在，給汽車輪胎的實際行駛狀態帶來了較大的影響。試驗表明，汽車輪胎的快速磨損和畸形磨損有相當一部分是由于車輪外傾角、前束角的大小匹配不合理造成的。下面將分析汽車前束角對輪胎自激振動的影響規律，所用參數見表9。

表9 仿真用前束角Tab.9 Simulation toe-in angle used

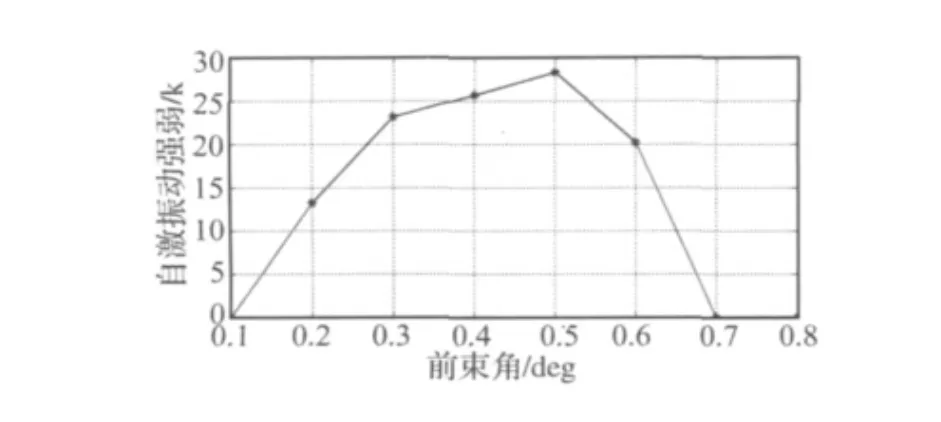
圖17 前束角對輪胎自激振動的影響Fig.17 Impact of toe-in angle on tire self－ excited vibration

圖17為不同前束角下的K值，由圖可知，汽車的前束角對輪胎自激振動的影響比較突出，在本文的仿真參數條件下，當汽車的前束角在0.2～0.6 deg范圍內時，輪胎產生自激振動，且在該范圍內隨著前束角的增大，自激振動的劇烈程度以大約0.5 deg為界限，先逐漸增大，再逐漸減小。前束角過小或過大時，輪胎胎面并不產生自激振動，這與實際情況相吻合。

2.2.5 汽車外傾角對輪胎自激振動的影響

汽車外傾角也會對輪胎自激振動產生影響，下面將分析汽車外傾角對輪胎自激振動的影響規律，所用參數見表10。

圖18為不同外傾角下的K值，由圖可知，輪胎胎面的自激振動對汽車的外傾角的敏感程度雖然并不如前束角那么強烈，但也不能忽視。在一定的外傾角范圍內，隨著外傾角增大，輪胎自激振動有加劇趨勢，當外傾角達到一定值后，輪胎胎面的自激振動將不再隨外傾角的增大而加劇，而是有所下降。所以合理的選取車輪的外傾角，也可以在一定程度上控制輪胎的自激振動，進而抑制輪胎的多邊形磨損。

表10 仿真用外傾角Tab.10 Simulation camber angle used

圖18 外傾角對輪胎自激振動的影響Fig.18 Impact of camber angle on tire self-excited vibration

3 結論

(1)輪胎胎面自激振動屬于“硬自激振動”，即只有在滿足一定條件下才會出現，行駛車速、輪胎載荷以及汽車的前束角和外傾角等都是比較重要的影響因素;

(2)一定參數條件下，只有當車速在一定范圍內時，輪胎胎面才能產生自激振動，車速過低或者過高均不會產生，前束角對自激振動的影響與車速類似，兩者都有一個對應于自激振動的取值范圍;

(3)在大載荷條件下，胎面自激振動比較劇烈，輪胎的多邊形磨損也會比較嚴重。

根據以上分析，本文提出以下控制輪胎自激振動及輪胎多邊形磨損的策略:

(1)盡量避開能夠產生自激振動的行駛車速范圍，避免長時間大負荷超載行駛，合理調整汽車前束角、外傾角等參數，盡量避開易導致發生自激振動的范圍;

(2)其他控制策略:從輪胎的結構和材料入手，研究并改善輪胎的自激振動特性，以降低多邊形磨損。

［1］ 龔慶壽.機床進給系統的自激振動［J］.湖南工程學院學報，2002，12(3):43－44.

［2］ McMillan A J.A non-linear friction model for self-excited vibrations［J］.Journal of Sound and Vibration，1997，205(3):323–335.

［3］ Sueoka A，Ryu T，Kondou T，et al.Polygonal wear of automobile tire［J］.JSME International Journal Series C，1997，40(2):209－217.

［4］ 李 勇，左曙光，雷 鐳，等.基于胎面側向振動的輪胎多邊形磨損機理分析［J］.同濟大學學報(自然科學版)，2011，39(1):100－104.

［5］ 楊憲武，左曙光，雷 鐳，等.基于胎面－路面摩擦自激的輪胎非線性振動建模仿真［J］.振動與沖擊，2010，29(5):211－214.

［6］ Zheng D.Prediction of tire tread wear with FEM steady state rolling contact simulation［J］.Tire Science and Technology，2003，31(3):189－202.

［7］ 王紀瑞.滾動汽車輪胎自激振動及其影響因素分析［D］.上海:同濟大學，2011.

［8］ 彭旭東，謝友柏，郭孔輝.輪胎摩擦學的研究與發展［J］.中國機械工程，1999(2):215－219

［9］ Canudas D W C，Oolsson H，Astrom K J，et al.A new model for control of systems with friction［J］.IEEE Transactions on Automatic control，1995，40(3):419－ 425.

［10］ 灰 晉，周 潔.影響輪胎磨損因素的探討［J］.輪胎工業，2002(22):629－630.

［11］ Heinrich G，Kluppel M，Friction R.Tread deformation and tire traction［J］.Wear，2008，265:1052－1060.

［12］ 彭旭東，郭孔輝，丁玉華，等.輪胎磨損的影響因素［J］.橡膠工業，2003，50(10):619－624.