基于譜單元方法的平板沖擊流固耦合研究

郭 君，張阿漫，楊文山，李 佳

(哈爾濱工程大學 船舶工程學院，哈爾濱 150001)

水下爆炸載荷作用下的艦船結構毀傷一直是國內外學者研究的熱點［1－3]，與之相對應的水下沖擊流固耦合問題主要是求解瞬態沖擊波激勵下結構的響應，其研究內容涉及到結構、材料、流體力學等諸多領域。當結構遭受水下沖擊波載荷作用時，可壓縮瞬態波在流體中傳播并撞擊到結構上，在結構濕表面處會發生繞射，如果結構是彈性的，且周圍水的靜壓力足夠低，散開的稀疏波可能會導致子區域內產生氣穴，我們稱之為氣穴現象［4]。產生氣穴區域的水的體積模量比未產生氣穴區域的水的體積模量要小好幾個數量級，呈現非線性特性。由于結構尺寸、入射波衰減長度和氣穴區域在空間尺寸上差別很大，氣穴會對近自由面結構如水面艦船產生很大影響，如果一個45 kg的HBX－1炸藥在水下爆炸，產生氣穴區域，產生的氣穴區域在水平上最長為489 m，深度上最大為9 m，其中船體尺寸為:寬9.1 m、高4.6 m、吃水 3.1 m。

為處理氣穴現象，Newton［5]提出了一種非常有效的計算方案來處理氣穴聲學流體，該方案采用位移勢作為流體域有限元方程中的主要變量，位移勢是一個標量。由于傳統流體有限元方程中采用的變量為位移矢量，位移矢量表達式中的變量是位移勢表達式中的未知量數目的三倍，而且不能自動對流體運動實行無旋處理，因此，與位移矢量相比，位移勢的選取具有相當大的優勢。Newton方案的第二個特點是應用了顯式時間積分方法。后來，Felippa和 DeRuntz［6]對 Newton的方法進行了擴展，對流固耦合方程進行三維表述，并對結構和流體進行有限元處理。然而，有限元方法采用的單元通常為低階單元，在解決波的傳播問題時會出現數值發散，要想得到準確的數值結果需要十分精細的網格，尤其當有氣穴現象出現時，網格細化更是尤為重要，從而導致計算量很大。為此，基于Felippa和DeRuntz的三維表述和結構有限元處理，本文引進譜單元對流體進行處理，以探索一種更為有效的水下爆炸流固耦合求解方法。文中采用基于勒讓德多項式的譜單元［7－8]，這是一種高階單元，采用高階單元可以不需要細化網格便獲得收斂性。此外，譜單元還可以很好地顯示波的傳播特性［9－10]。譜單元方法綜合了有限元方法的幾何靈活性和譜方法的計算高精度性，在保證精度的同時還能提高計算速度。

1 譜單元數值模型

1.1 控制方程

在推導產生氣穴的聲學流體的控制方程時，首先采用雙線性模型［11]來考慮流體中的氣穴現象。雙線性模型是一種簡單合理的流體構成模型，在這種模型中，當壓縮率(負體積應變)為正時，體積模量為水作為聲學介質時的值;當壓縮率為負時，體積模量為零。雙線性狀態方程如下:

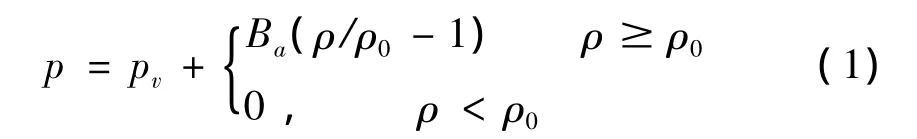
式中，Ba是不存在氣穴時的體積模量是流體的總壓力，pv是溫度T0時水的蒸汽壓力，ρ0是溫度T0飽和流體的密度是瞬時密度是流體質點的位置矢量，t表示時間。假定在整個討論域內T0、ρ0和ρv是常量，定義，其中c是無氣穴聲學流體中的聲速，S=(ρ/ρ0－1)是總的壓縮率，通過這些定義可將狀態方程改寫為:

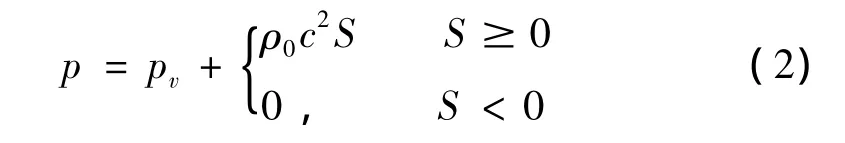
假設流體是無旋的，且忽略粘性的影響，從而保證了流場用勢來進行表述。用位移勢來表示流場的位移為，其中和分別為流體質點的總位移和平衡位移為位移勢是流體質點的整體位置矢量。

根據流體的連續性方程和歐拉運動方程，并引用位移勢，可得到流體的平衡方程如下:

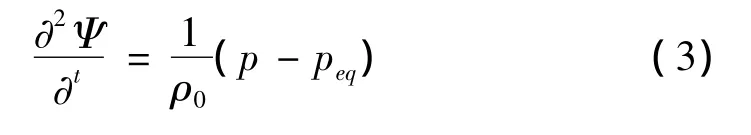
其中peq=－ρ0(Vg+h)是平衡壓力。

式(2)與式(3)便構成了流體的控制方程組，利用關系式peq=pv+ρ0(Vg+h)，并定義壓縮率s=ρ0(SSeq)，位移勢 ψ =ρ0Ψ，則根據式(2)和式(3)，控制方程組可寫為:

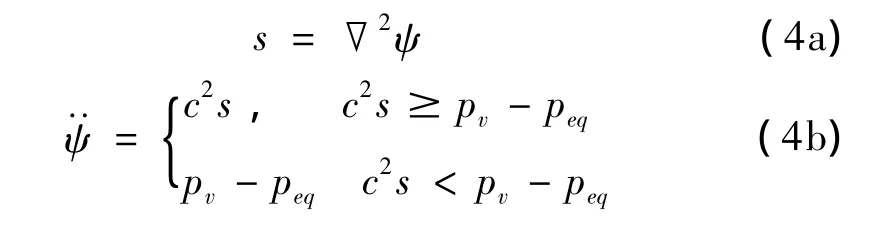
式中為動態壓縮率為動態位移勢為流體節點坐標，peq為水的平衡壓力，c為水中的聲速，pv為水的汽化壓力，由于pv比平衡壓力小很多，故可忽略不計，上標點表示變量對時間的導數。

1.2 譜單元空間離散

與有限元離散相同，采用等參元對整個流體域進行離散，將其離散成ne個六面體單元，則每個單元的幾何形狀可表示為:

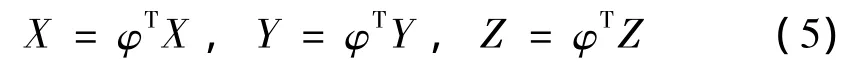
φ仍然采用三線性函數。

然而，與有限元離散不同的是，在自然坐標系內，將壓縮率s和位移勢ψ離散為:

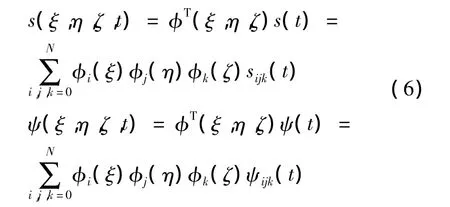
式中:φ為由N階多項式構成的基函數，s為每個單元內(N+1)3個節點分別對應的壓縮率，ψ為每個單元內(N+1)3個節點分別對應的位移勢，ξ，η，ζ為單元的自然坐標(－1≤ξ，η，ζ≤1)。

譜單元方法和有限元方法的最大區別在于φi的選擇，在有限元法中，φi取為與幾何變換相同的三線基函數，而在譜單元方法中，φi取為由勒讓德多項式構成的一維拉格朗日插值函數［12]，這也是目前國內外應用最廣泛最有效的譜單元基函數:

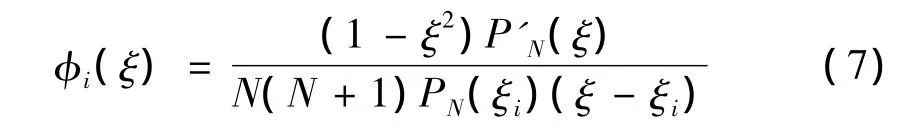
式中 PN為 N階勒讓德多項式，ξi為第 i個 Gauss-Lobatto-Legendre積分點，其值為下式的根:

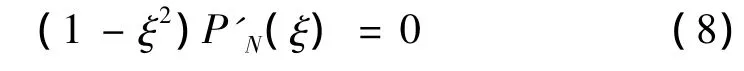
可以證明，表達式(6)滿足下列關系式:

式中δij為克羅內克δ。

用標準伽遼金法對控制方程式(4a)進行離散，用φ左乘式(4a)，在流體域上對方程積分，并應用格林第一公式可得:

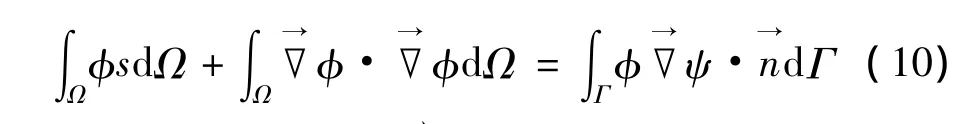
式中Q，H，b分別為:

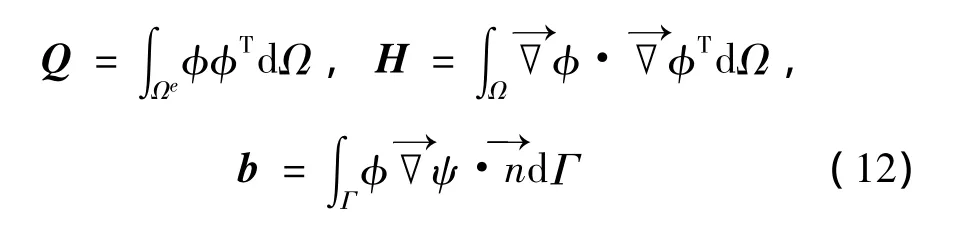
2 平板的水下爆炸流固耦合研究

2.1 計算模型

為驗證所建立的數值模型的準確性，需將數值解與準確解進行對比。這里采用的計算模型為經典的Bleich-Sandler平板模型，如圖4所示，平板位于半無限長流體柱上，遭受平面步指數沖擊波作用，平板速度響應的解析解可由特征法得到［11]。

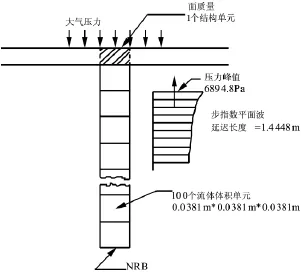
圖1 Bleich-Sandler平板模型Fig.1 Bleich-Sandler plate model

計算模型的物理屬性為:大氣壓力為Patm=0.101 MPa，重力加速度為g=9.81 m/s2，流體密度為 ρ=998 kg/m3，流體中聲速為 c=1 450 m/s，流體長度為3.81 m，由100個等邊長的六面體單元構成，平板密度為ρ=5 698 kg/m3，邊長為0.038 1 m，由一個單元構成，平面步指數波的壓力峰值為p0=0.71 MPa，延遲時間為τ=0.1 ms，在沖擊波波陣面距離平板一個流體網格時開始積分計算［13]。

2.2 計算結果及討論

平板中心的速度時歷曲線如圖2所示，實線顯示的是由譜單元法得到的數值解，圓點和三角形點則分別表示的是由特征法得到的考慮氣穴和不考慮氣穴時的平板中心速度響應的解析解。分別計算了人工阻尼β 取作0.25、0.50、0.75 和 1.0 的四種情況，臨界時間步根據2.3節中的表述進行計算，計算時間步取作臨界時間步的0.75倍。

圖2給出了人工阻尼β取不同值時平板中心的速度隨時間變化的曲線，對計及氣穴和不計氣穴的兩種情況進行了計算，并分別與Bleich-Sandler的解析解進行對比。從圖2可以看出，由譜單元方法得到的數值結果與Bleich-Sandler解析解吻合較好，同時人工阻尼β對結構的響應幅值和響應時間幾乎沒有影響，圖2(a)中曲線的微小振蕩是由流體網格的瞬時擾動所引起，隨著β的增加，振蕩逐漸消失。從圖2還可以看出，氣穴的存在不會改變速度的峰值，但會延長速度的衰減時間，從而延長載荷對結構的作用時間，對結構產生更大的破壞。

3 譜單元方法和有限元方法的對比研究

如前面部分提到，譜單元法相比有限元法具有很多優點，這節將分別從精度和效率上對此進行討論。

3.1 計算模型

如圖3所示，計算模型為位于流體柱上的一個兩自由度的質量彈簧振子，遭受平面步指數沖擊波作用，圖中質量塊m1表示船體外板，質量塊m2表示船體內部的結構和設備，兩質量塊由剛度系數為k的彈簧連接，m1和m2的位移分別用u1(t)和u2(t)表示，速度分別用V1(t)和V2(t)表示。

計算模型的物理屬性為:大氣壓力為Patm=0.101 MPa，重力加速度為 g=9.81 m/s2，質量塊由邊長為0.3 m的正方形板表示，m1=76.9 kg，m2=384.5 kg，彈簧剛度系數為k=94 870 kg/s2，流體密度為ρ=1 026 kg/m3，流體中聲速為c=1 500 m/s，流體長度為3 m，壓力峰值為 p0=16.2 MPa，延遲時間為 τ=0.42 ms，沖擊波波陣面距m1的距離為dinc=0.3 m時開始進行積分計算。

圖2 平板中心速度隨時間的變化曲線Fig.2 The flat center speed changing with time curve

3.2 計算結果及討論

有限元方法作為一種數值方法，已經被廣泛應用于水下沖擊問題的求解中，并證明具有一定的精度［6]，針對3.1 節的物理模型，我們采用由高度細化的有限元網格(24 000個等長單元)產生的有限元解作為基準解，討論譜單元方法(SEM)和有限元方法(FEM)在不同細化程度時的精度。

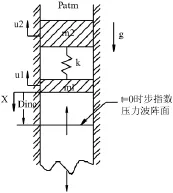
圖3 計算模型Fig.3 Calculation Model

分別采用譜單元方法和有限元方法計算m1的速度響應，并分別與基準解對比。不同細化程度時質量塊m1的速度隨時間的變化曲線如圖4所示。

圖4給出了分別采用譜單元方法和有限元方法在不同細化程度下算得的質量塊m1的速度響應曲線，分別將有限元解和譜單元解與基準解進行對比分析。誤差系數見表1。

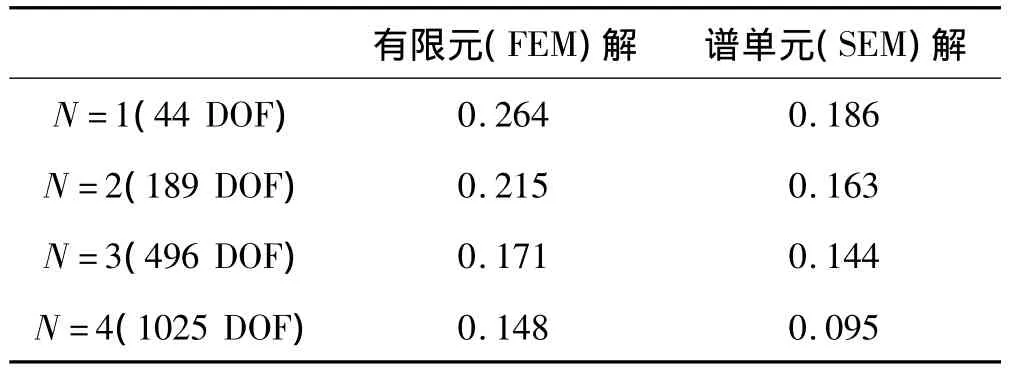
表1 有限元解及譜單元解與基準解之間的誤差系數cTab.1 Finite element solution and the spectral element solution and the error c between the coefficient of benchmark solutions

圖4 結構的速度響應對比曲線Fig.4 The comparison curve of the velocity response of the structure

從表1給出的誤差系數可以看出，譜單元方法和有限元方法所產生的誤差均隨著細化階數的升高逐漸減小，收斂于基準解。然而，在細化階數相同(系統所具有的自由度相同)的條件下，譜單元方法得到的數值解更接近基準解，因此，與有限元方法相比，譜單元方法具有更高的精度。

從表1還可以看出，在誤差相同的條件下，譜單元方法需要的自由度較少。例如:若將c=0.15設為允許誤差，用譜單元方法需要不足496個自由度便能達到允許誤差，而用有限元方法需要的自由度數則接近1 025。因此，譜單元方法在精度提高的同時可以大大減少計算所需要的自由度數，具有更高的計算效率。

4 結論

本文基于流體雙線性構成關系考慮流體中可能發生的氣穴現象，采用基于勒讓德多項式的譜單元方法建立了水下爆炸流固耦合動力學模型，應用經典的平板沖擊問題對模型進行了驗證。分別采用譜單元方法和有限元方法對彈簧－平板模型進行水下爆炸流固耦合的求解，基于廣義誤差系數對譜單元方法和有限元方法進行對比研究，得到以下結論:

(1)采用譜單元方法對Bleich-Sandler平板水下爆炸流固耦合問題進行計算，得到的數值解與Bleich-Sandler的基本解吻合良好，譜單元方法能較好地應用于水下爆炸流固耦合問題的求解中。

(2)流體中產生氣穴時，未產生氣穴的流體區域將結構與產生氣穴的流體區域分開，形成流體堆積。氣穴區域閉合時流體中形成正壓力沖擊作用，產生二次加載現象，從而對結構產生更嚴重的破壞，因此在計算中應予以考慮。

(3)人工阻尼對結構響應具有光順作用，但基本不會影響結構的響應幅值和響應時間。隨著人工阻尼的增加，由流體網格瞬時擾動引起的結構響應的振蕩逐漸消失。

(4)與有限元方法相比，在同樣網格細化的條件下，譜單元方法具有更高的精度;在誤差相同的條件下，譜單元方法所需的自由度數大大小于有限元方法所需的自由度數。因此，與有限元方法相比，譜單元方法在提高精度的同時，能大量節省計算時間。

［1] 牟金磊，朱 錫，黃曉明，等.水下爆炸氣泡載荷在加筋板塑性變形中的作用［J] .振動與沖擊，2010，29(5):74－77.

［2] 李海濤，朱 錫，趙小龍，等.箱形梁在水下近距非接觸爆炸作用下的整體毀傷研究［J] .振動與沖擊，2010，29(3):158－161.

［3] Ramajeyathilagam K，Vendhan C P，Bhujanga Rao V.Nonlinear transient dynamic response of rectangular plates under shock loading［J] . International Journal of Impact Engineering，2000，24:999 －1015.

［4] Kennard E H.Cavitation in an elastic liquid［J] .Physical Review，1943，63(5/6):172－181.

［5] Newton R E.Finite element analysis of shock-induced cavitation，1980. Preprint 80 － 110， ASCE Spring Convention.

［6] Felippa C A，DeRuntz J A.Finite element analysis of shockinduced hull cavitation［J] .Computer Methods in Applied Mechanics and Engineering，1984，44:297－337.

［7] Ronquist E M，Patera A T.A legendre spectral element method for the Stefan problem［J] .International Journal for Numerical Methods in Engineering，1987，24:2273－2299.

［8] Maday Y，Patera A T.Spectral element methods for the incompressible Navier-Stokes equations［J] .The American Society of Mechanical Engineers，New York，1989.

［9] Komatitsch D，Vilotte J P.The spectral element method:An efficient tool to simulate the seismic response of 2D and 3D geological structures［J] .Bulletin of the Seismological Society of America，1998，88(2):368－392.

［10] Mulder W A.Spurious modes in finite-element discretizations of the wave equation may not be all that bad［J] .Applied Numerical Mathematics，1999，30:425 445.

［11] Bleich H H，Sandler I S.Interaction between structures and bilinear fluids［J] .International Journal of Solids and Structures，1970，6:617－639.

［12] Ronquist E M，Patera A T.A Legendre spectral element method for the Stefan problem［J] .International Journal for Numerical Methods in Engineering，1987，24:2273－2299.